Triangle Clipping

메시가 CPU와 GPU를 거쳐 최종 화면에 그려지기까지의 여정을 단계별로 정리

순서는 큰 것(오브젝트,메쉬)부터 해서 다 정리한 다음 가장 작은 단위(픽셀)로 처리하게 됩니다.

체에 다 걸러진 남은것만 하나하나 처리하는게 가장 빠르니까요.

CPU

CPU에서는 오브젝트 단위에서 처리될 수 있는 것들을 처리합니다.

정리

메시(mesh) → 절두체 컬링(Frustum Culling) → 오클루전 컬링(Occlusion Culling)→ GPU

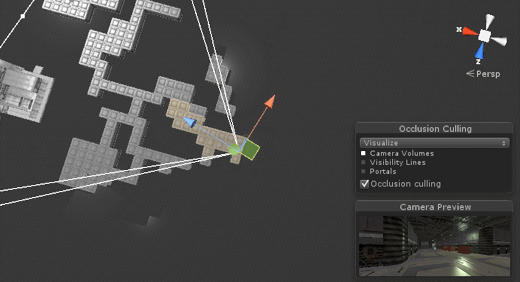
절두체 컬링(회색)과 오클루전 컬링(갈색). 최종적으로 갈색 오브젝트만 남는다

GPU

GPU에선 이제 정점데이터를 받아

정점단위 처리를 우선 진행하고, 래스터화를 진행하며, 픽셀단위 처리를 하게 됩니다.

정리

정점 버퍼(Vertex) →

[버텍스 단위] 좌표 변환, 후면 컬링(BackFace Culling) 및 삼각형 클리핑 →

래스터화 →

[픽셀 단위] 깊이 버퍼 테스트(Z-Test) → 스텐실 테스트 → 알파블렌딩 →

후 처리(Post Processing) → 노출

Known Issue

기존 과제물(절두체 컬링)을 테스트하다보면 가끔 오류가 나는 현상이 발생합니다.

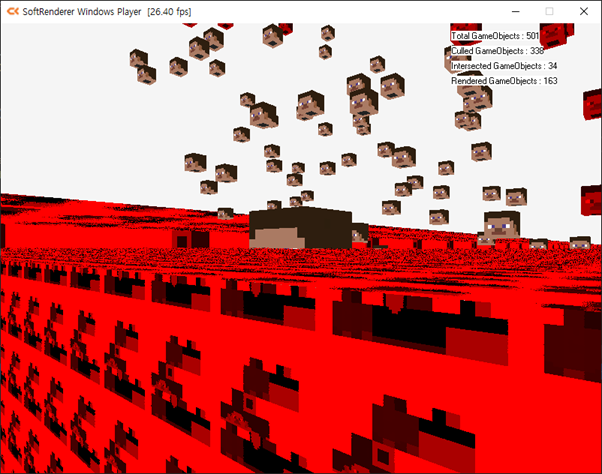
8%20Triangle%20Clipping%20c2331e1b7c97414a96a0cb9b3e007609/Untitled%201.png

그 이유는 단순합니다.

버텍스가 카메라 뒤에 있을 때 역으로 투영이 되기 때문에 다른 삼각형이 만들어지기 때문이죠.

그렇다면 이렇게 벗어나는 삼각형들을 처리하는 방법은 없을까요?

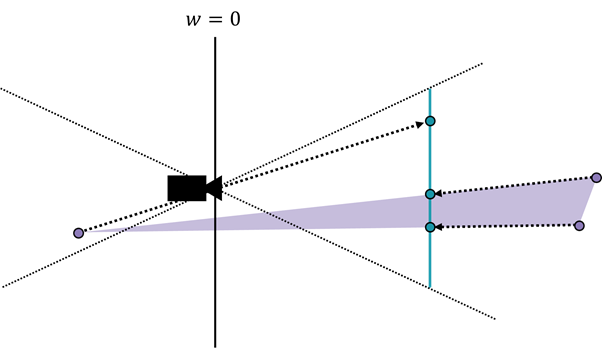
Untitled

정답은 ‘있다’ 입니다.

평면에 대한 삼각형의 분할

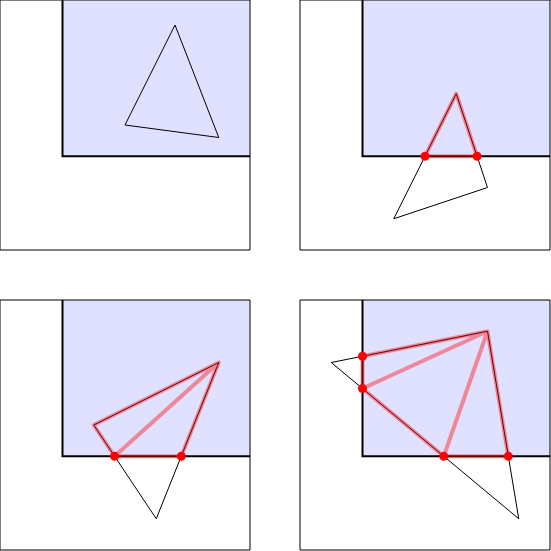
삼각형 클리핑

위 이미지는 평면에서의 삼각형을 분할하는 이미지입니다. 최종적으로 저희가 다룰 내용이죠.

결국 잘랐을때 점이 4개면 두개의 삼각형으로, 아니라면 대충 알아서 라는 방식이죠.

어떤 예시가 있을까요? 음 … 삼각형을 색칠할 때,

스캔라인 방식으로 처리하기 위한 삼각형 분할을 생각하면 편합니다.

스캔라인에서의 삼각형 분할

사실 삼각형을 분할한다하면 갑자기 엄청 당황스럽지만, 공유하는 하나의 선에 대해,

반복되는 하나의 선씩 자른다고 생각하면 정말 간단합니다.

두 선의 교점을 구하는 것이에요! 선형적으로 말이죠.

자 그러면 이제 두가지 경우의 수, 한 선분과 하나의 삼각형으로 나올 수 있는 점의 수를 생각해 봅시다.

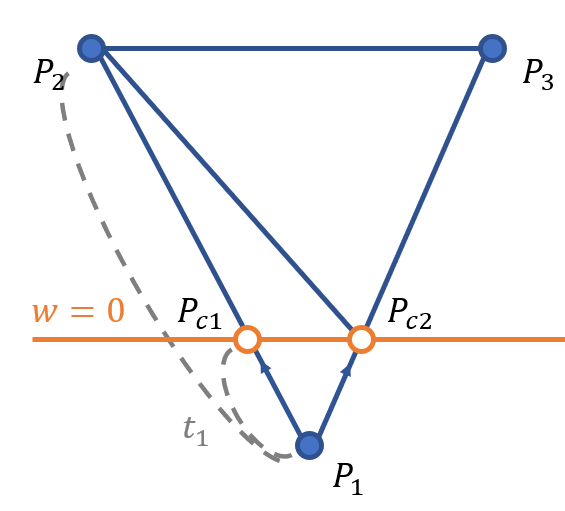
case 1. 카메라 뒤로 점이 하나 있는 경우

이 경우 최종적으로 점이 4개가 나오는 경우 이므로, 삼각형 두 개로 분할합니다.

Untitled

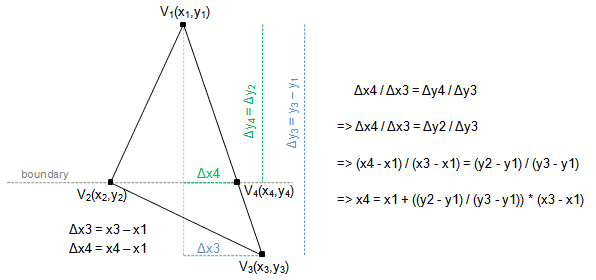
아핀조합, 선형보간을 떠올리며

두 변에 대해 변에 속한 점을 구하는 식을 을 다음과 같이 설정합니다.

let, \\ P_{c1} = P_1 \cdot( 1- t_1 ) + P_2 \cdot t_1 \\ P_{c2} = P_1 \cdot( 1- t_2 ) + P_3 \cdot t_2

해당 자르는 선분은 거리 0위치에 존재하므로,

사영공간에서 잘라진 삼각형의 마지막 요소 $w$ 값은 0이 됩니다.

따라서 두 점의 $w$ 값을 각각 $w_1, w_2$ 로 표현하여 다음과 같은 직선의 방정식이 나옵니다.

w_1\left(1-t_1\right)+w_2t_1\ =\ 0 \\ t_1=\ \frac{w_1}{w_1-w_2}\ \\

식은 복잡하지만 결국 t1은 선분에서의 어느정도 위치에 있는지에 대한 비율값입니다.

이에 따라 정점의 값들을 보간해줍니다. UV,색상,위치 등등

그렇게 나온 네 점을 통해 두개의 삼각형을 제작하여줍니다.

case 2. 카메라 뒤로 점이 두 개 있는 경우

이 경우 최종적으로 세개의 점이므로,분할 없이 정점만 갱신시켜줍니다.

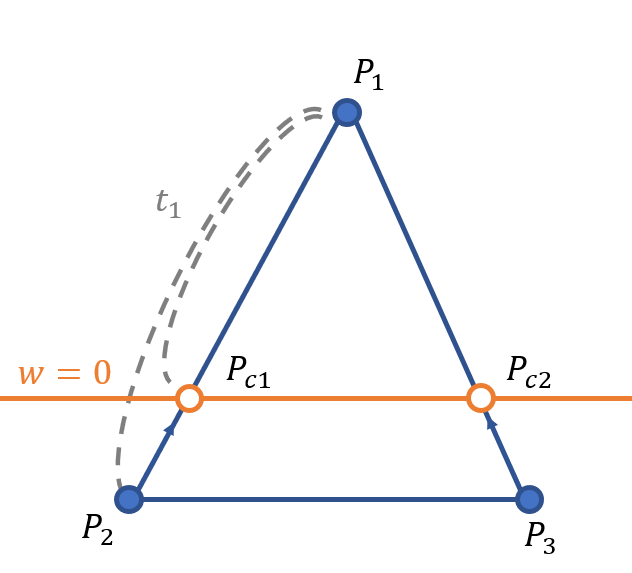
Untitled

비율을 구하는 것도 동일한 방법이니 패스하도록 하겠습니다.

절두체에 대한 삼각형의 분할

사실 생각해보면 $w=0$ 이 아닌 다른 직선의 방정식도 얼마든지 분할이 가능합니다.

직선에서 부터의 점의 거리를 구할 수 있으니까요.

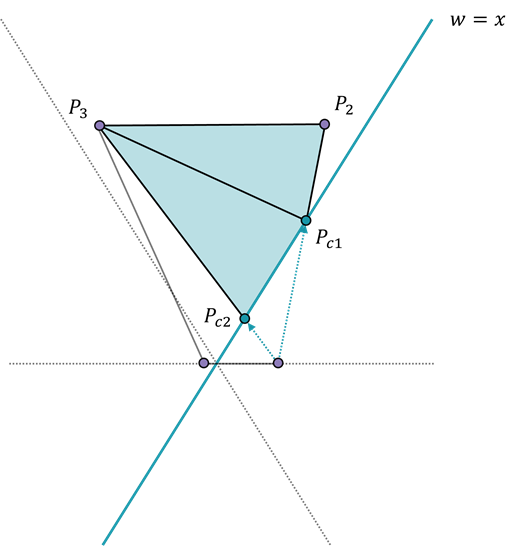
절두체의 평면에 대한 삼각형의 분할

예를 들어 위의 이미지를 참고로 해볼까요?

위 청록색 선분으로 표시한 면이 우측면이라 가정할 때,

NDC공간에서 x좌표만 본다면 1인 부분입니다.

그러면 클립좌표에서 생각한다면… w로 나눠줬을 테니, 다음과 같이 되겠죠?

\frac{x}{w}=1\quad\quad \therefore x=w

그러면 이제 비율값을 다시 구해봅시다.

겁먹을 것 없어요. 단순히

w_1\left(1-t_1\right)+w_2t_1\ =\ 0

에서 x에 대한 정보가 추가될 뿐입니다.

w_1\left(1-t_1\right)+w_2t_1 = x_1\left(1-t_1\right)+x_2t_1

정리하면

따라서 매개변수 값을 다음과 같이 얻을 수 있습니다.

t_1=\frac{w_1-x_1}{(w_1-x_1)-(w_2-x_2)}

그러면 걸러줄 녀석들만 판별만 해주면 되겠죠?

\frac{x}{w}>1 \quad or \quad x > w

자. 노가다 시간입니다.

Untitled

손으로 계산했던 그 노가다를 하면서 깨달았습니다. 이럴 필요가 없었다는 것을.

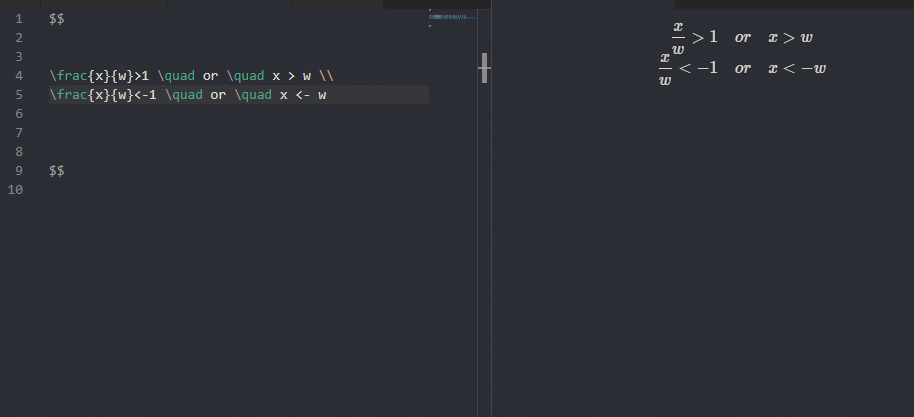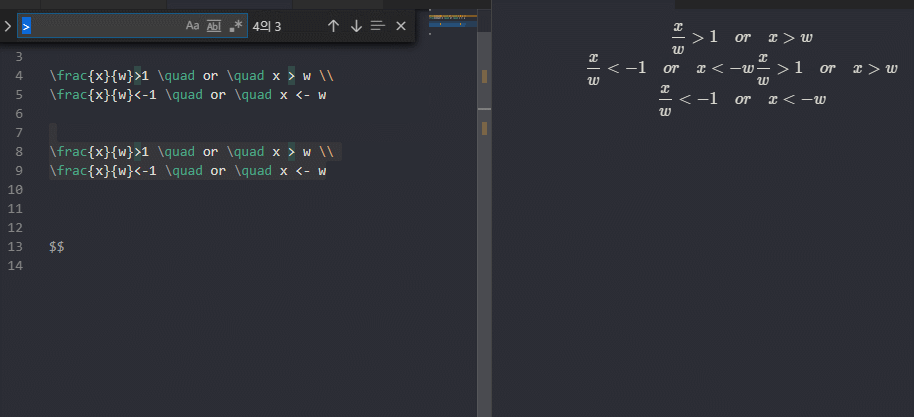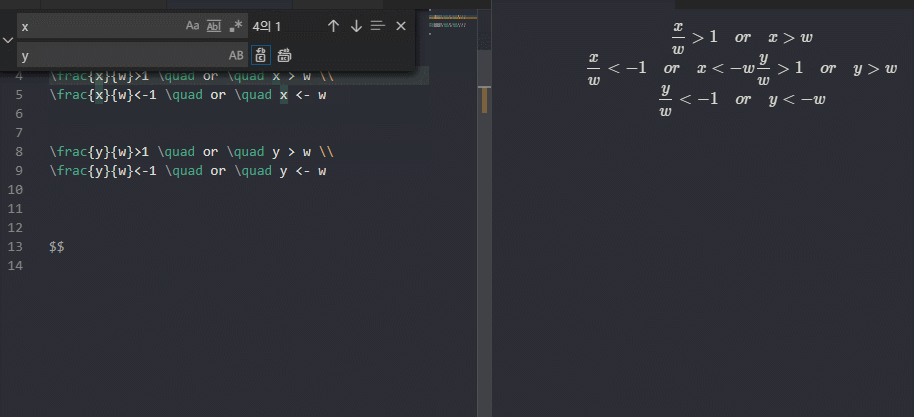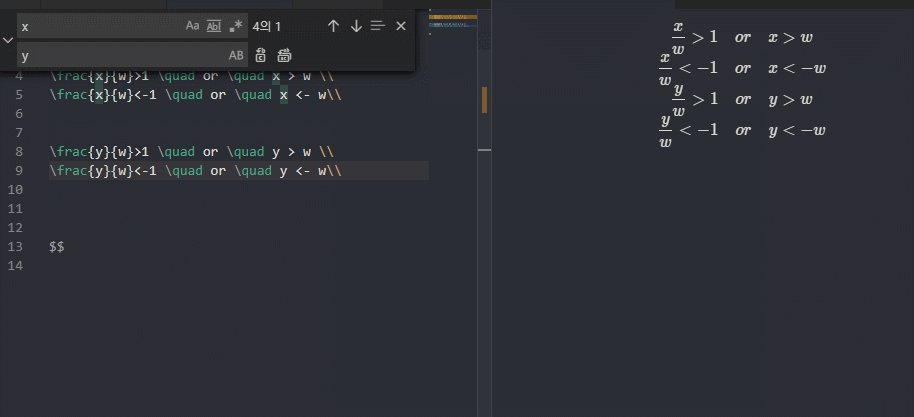
사실 수식은 타이핑하는게 더 쉽습니다

오른쪽 평면(X+)

\frac{x}{w}>1 \quad or \quad x > w

t = \frac{p_{1_w}-p_{1_x}}{(p_{1_w}-p_{1_x})-(p_{2_w}-p_{2_x})}

왼쪽 평면(X-)

\frac{x}{w}<-1 \quad or \quad x <- w\\

t = \frac{p_{1_w}+p_{1_x}}{(p_{1_w}+p_{1_x})-(p_{2_w}+p_{2_x})}

위쪽 평면(Y+)

\frac{y}{w}>1 \quad or \quad y > w \\

t = \frac{p_{1_w}-p_{1_y}}{(p_{1_w}-p_{1_y})-(p_{2_w}-p_{2_y})}

아래쪽 평면(Y-)

\frac{y}{w}<-1 \quad or \quad y <- w\\

t = \frac{p_{1_w}+p_{1_y}}{(p_{1_w}+p_{1_y})-(p_{2_w}+p_{2_y})}

원평면(Z+) (단, NDC좌표계에서 [-1,1]을 가진다 가정할 때)

\frac{z}{w}>1 \quad or \quad z > w \\

t = \frac{p_{1_w}-p_{1_z}}{(p_{1_w}-p_{1_z})-(p_{2_w}-p_{2_z})}

근평면(Z-)

\frac{z}{w}<-1 \quad or \quad z <- w\\

t = \frac{p_{1_w}+p_{1_z}}{(p_{1_w}+p_{1_z})-(p_{2_w}+p_{2_z})}

순서도 정리

절두체 처리할 때 했던 그거 아시죠?

텍스트만 수정할 것입니다.

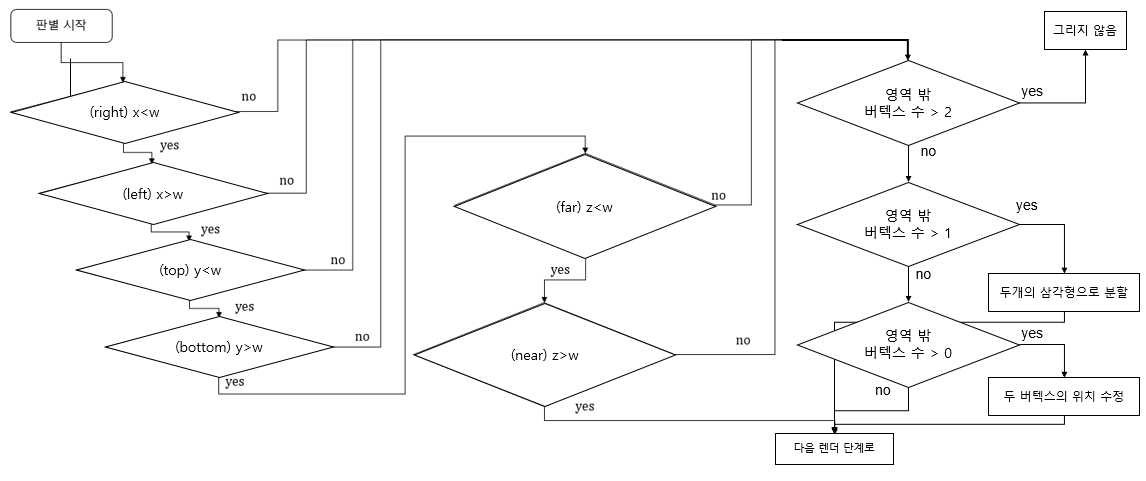
Untitled

활용예제

굳이 그러면 화면의 끝을 자를려는게 아니라면 w값을 사용해 자를 필요가 있을까? 하여

w값이 아닌 대각선으로 잘라보았습니다.

이때, 대각선의 공식은 x - y = 0, x + y = 0 이므로 이를 대입해 줍니다.

  
//at PerspectiveTest.h
	
static auto TestFuncPCross = [](/assets/const Vertex3D& InVertex)
{
	return  InVertex.Position.X - InVertex.Position.Y < 0;
};

static auto EdgeFuncPCross = [](/assets/const Vertex3D& InStartVertex, const Vertex3D& InEndVertex) {
	float p1 = 0 - (InStartVertex.Position.X - InStartVertex.Position.Y);
	float p2 = 0 - (InEndVertex.Position.X - InEndVertex.Position.Y);
	float t = p1 / (p1 - p2);
	return InStartVertex * (1.f - t) + InEndVertex * t;
};

static auto TestFuncNCross = [](/assets/const Vertex3D& InVertex)
{
	return  InVertex.Position.X + InVertex.Position.Y > 0;
};

static auto EdgeFuncNCross = [](/assets/const Vertex3D& InStartVertex, const Vertex3D& InEndVertex) {
	float p1 = 0 + (InStartVertex.Position.X + InStartVertex.Position.Y);
	float p2 = 0 + (InEndVertex.Position.X + InEndVertex.Position.Y);
	float t = p1 / (p1 - p2);
	return InStartVertex * (1.f - t) + InEndVertex * t;
};

빈공간이 남길래 만화경스럽게 만들어보았습니다.

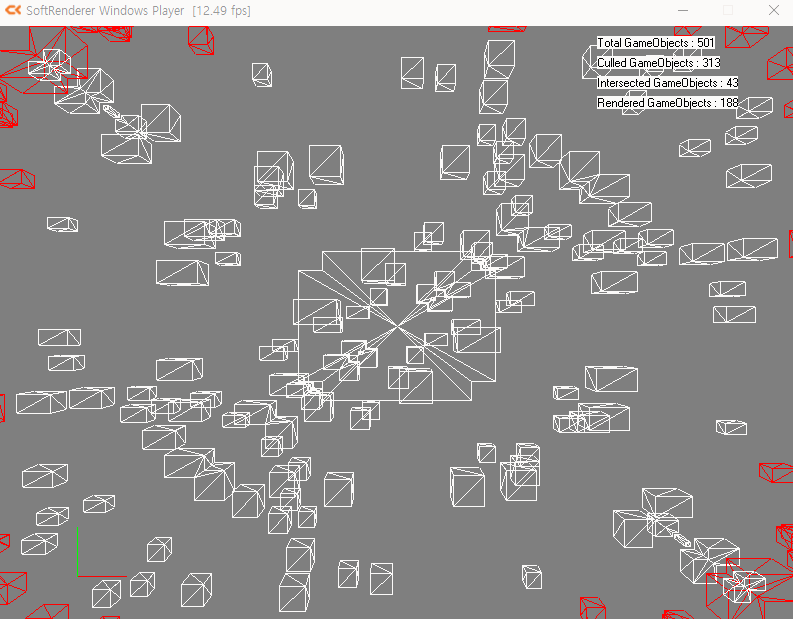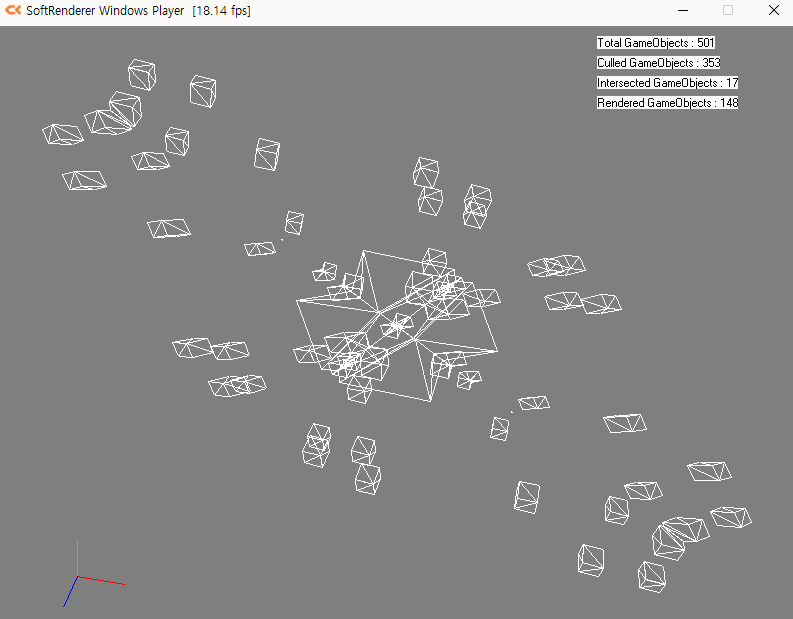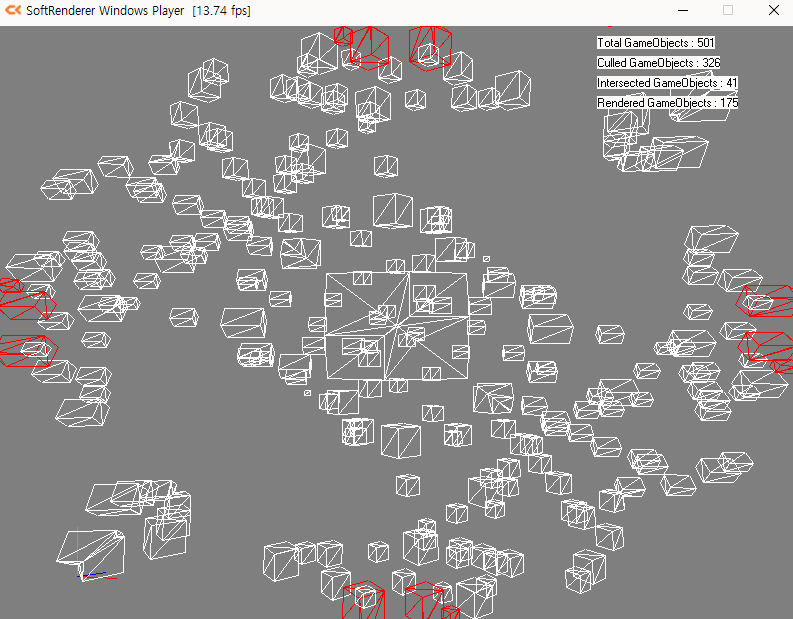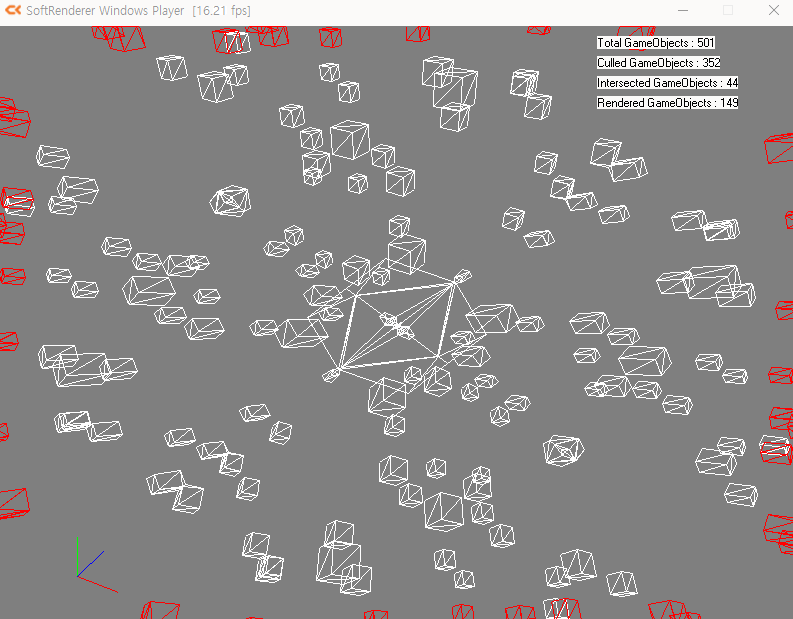
포스트프로세스처럼 렌더된 이미지 따와서 할까 하다가 종횡비 보간 문제가 귀찮아져서

버텍스를 수정하였습니다.

근데 이게 돌려서 뒤집으면 되는거 아님? 했더니 돌려서 뒤집으면 면도 뒤집힙니다.

그래서 뒷면을 그리기에, 인덱스버퍼를 뒤집어서 처리하였습니다.

(하하 면을 뒤집을려면 순서를 바꾸면 되는게지!)

  
//in DrawMesh3D at SoftRenderer3D.cpp

std::vector<Vertex3D> newVts;
for (auto& v : tvs)
{
	Vertex3D newVertexL = v;
	newVertexL.Position = InverseUpdown* rotMatL * v.Position;
	newVts.push_back(newVertexL);
}

for (auto& v : tvs)
{
	Vertex3D newVertexR = v;
	newVertexR.Position = InverseUpdown* rotMatR * v.Position;
	newVts.push_back(newVertexR);
}

std::reverse(newVts.begin(), newVts.end());

for (auto& v : tvs)
{
	Vertex3D newVertexU = v;
	newVertexU.Position = rotMatU * v.Position;
	newVts.push_back(newVertexU);
}

size_t triangles2 = newVts.size() / 3;
for (size_t ti = 0; ti < triangles2; ++ti)
{
	size_t si = ti * 3;
	std::vector<Vertex3D> sub(newVts.begin() + si, newVts.begin() + si + 3);
	DrawTriangle3D(sub, InColor, FillMode::Color);
}

…도망치겠습니다

8. Triangle Clipping

메시가 CPU와 GPU를 거쳐 최종 화면에 그려지기까지의 여정을 단계별로 정리

CPU

GPU

Known Issue

평면에 대한 삼각형의 분할

절두체에 대한 삼각형의 분할

오른쪽 평면(X+)

왼쪽 평면(X-)

위쪽 평면(Y+)

아래쪽 평면(Y-)

원평면(Z+) (단, NDC좌표계에서 [-1,1]을 가진다 가정할 때)

근평면(Z-)

순서도 정리

활용예제

Further Reading

1. 3D Transform

2. Gimbal-Lock & Cross Product

3.Backface Culling & Rodrigues rotation