Frustum Cull And Bounding Volume
절두체 컬링(Frustum Cull)
저번주차에 저희는 그렇게 절두체 내부에 있는 오브젝트를 판별하는 식을 나타내보았습니다.
그렇게 렌더링하기 전에 오브젝트의 위치가 화면 내에 있는지 판별하여, 쓸데없는 연산을 패스하는 처리를 하였습니다.
known issue
- 화면종횡비에 따른 절두체 면이 아니여서 화면과 다른 부분이 발생
- 오브젝트 중심이 화면을 벗어나는 즉시 그리기가 중단됨(끄트머리가 남아있어도)
하지만 수학적으로 처리하였기때문에 이번에는 행렬적으로 처리해 봅시다.
투영행렬로부터 절두체를 구성하는 6개의 평면의 방정식 유도
let,NDCcoord(nx,ny,nz),Clipcoord(x,y,z,w)절두체 안에 있는 최종 점의 범위는 UV와 같이 -1~1입니다.
즉 나타내면 다음과 같습니다.
−1≤nx≤1−1≤ny≤1−1≤nz≤1 −1≤wx≤1−1≤wy≤1−1≤wz≤1![Untitled]()
양변에 w를 취해서 식을 정리하고
−w≤x≤w−w≤y≤w−w≤z≤w원근 투영 행렬 리마인드하자면 다음과 같습니다.
P⋅ v=ad0000d0000n−fn+f−100n−f2nf0vxvyvz1=xyzw행렬의 곱은 내적과 같으므로, 각 행의 내적으로 표현한 후,
아까전에 취했던 식에 대입해봅니다.
Prow1⋅vProw2⋅vProw3⋅vProw4⋅v=xyzw ∴−Prow4⋅ v≤Prow1⋅ v≤Prow4⋅ v−Prow4⋅ v≤Prow2⋅ v≤Prow4⋅ v−Prow4⋅ v≤Prow3⋅ v≤Prow4⋅ v6개의 식으로 쪼개고,
(Prow4+Prow1)⋅ v≥0(Prow4−Prow1)⋅ v≥0(Prow4+Prow2)⋅ v≥0(Prow4−Prow2)⋅ v≥0(Prow4+Prow3)⋅ v≥0(Prow4−Prow3)⋅ v≥0끝입니다.
(사실 끝은 아니죠 아래를 진행해야하니까)
절두체 컬링을 구현하기 위해 필요한 방정식으로의 전환
v = (x,y,z,1), 괄호안의 벡터성분을 (a,b,c,d)로 둔다면
let v=(x,y,z,1)let (Psome+Pthing)=(a,b,c,d) ax+by+cz+d≥0마지막으로 정규화를 진행한 다음, 컬링에 사용하기 위해 면의 방향을 거꾸로 변경한다면?
−(a2+b2+c2ax+by+cz+d)>0완벽합니다.
행렬로 만들어진 평면의 방정식과 저번글의 직접계산한 식의 일치 검증
pf,cos2θy+sin2θz>0is−(Prow4−Prow2)⋅v>0−(Prow4−Prow2)⋅v=−(−z−dy)>0,d=tan2θ1∴sin2θcos2θy+z>0∴cos2θy+sin2θz>0만약 하나의 평면에 대해서 처리한다면 위와 같이 처리하겠는데…
6개를 해야합니다 6개를…!! 공장제 기계공업을 돌리고 싶은 갯수입니다.
…
일단 식들을 다시 가져옵시다.
−(Prow4+Prow1)⋅ v≤0−(Prow4−Prow1)⋅ v≤0−(Prow4+Prow2)⋅ v≤0−(Prow4−Prow2)⋅ v≤0−(Prow4+Prow3)⋅ v≤0−(Prow4−Prow3)⋅ v≤0대입하기위한 행렬의 행도 긁어옵시다. 이번엔 식으로.
Prow1=(ad,0,0,0)Prow2=(0,d,0,0)Prow3=(0,0,n−fn+f,n−f2nf)Prow4=(0,0,−1,0)대입해서 식을 정리해줍니다.
−(ad,0,−1,0)⋅ v≤0−(−ad,0,−1,0)⋅ v≤0−(0,d,−1,0)⋅ v≤0−(0,−d,−1,0)⋅ v≤0−(0,0,n−f2f,n−f2nf)⋅ v≤0−(0,0,−n−f2n,−n−f2nf)⋅ v≤0v를 다음과 같이 설정할 때,
let v=(x,y,z,1)6개의 평면은 다음과 같습니다.
−dx+az≤0dx+az≤0−dy+z≤0dy+z≤0n−f2fz+2fn=2f(z+n)≤0n−f−2nz−2nf=−2n(z+f)≤0여기서 이제 저 행렬의 세부값들을 정리해봅시다
d=tan2θ1a=widthheight(종횡비)그러면 이렇게 식이 나옵니다.
−cos2θx+sin2θaz≤0cos2θx+sin2θaz≤0−cos2θy+sin2θz≤0cos2θy+sin2θz≤0z+n≤0−z−f≤0대조해볼까요?(저번 게시글을 그대로 긁었습니다)
Znear→z+near=0Zfar→−z−far=0 Yup→(sin(2π−2θ))y+(cos(2π−2θ))z=(cos2θ)y+(sin2θ)z=0Ydown→(−sin(2π−2θ))y+(cos(2π−2θ))z=(−cos2θ)y+(sin2θ)z=0 Xleft→(−sin(2π−2θ))x+(cos(2π−2θ))z=(−cos2θ)x+(sin2θ)z=0Xright→(sin(2π−2θ))x+(cos(2π−2θ))z=(cos2θ)x+(sin2θ)z=0컬링용이니 대충 맞네요(XY의 순서가 다른것은…알아서 읽어주세요)
바운딩 볼륨(Bounding Volume)
아.. 저번주에 바운딩 볼륨과 관련하여 말한것이 있는데, 결국 싸게싸게 절두체안에 존재하는지(그려야하는지) 체크하기 위한 방법들이 있습니다.
예전에 cocos-2dx 처음 배울땐 aabb obb 상당히 많이 들었었는데 오랜만에 들으니까 친숙하네요.
![Untitled]()
![Untitled]()
이것말고도 다른 충돌탐지방법이 아주 많지만,
(Convex-hull을 만들어서 GJK알고리즘을 돌리고(교차판정) EPA 알고리즘(침투분리)을 돌린다거나..)
비쌉니다. 정확히는 큰 오버헤드가 발생한다고 하죠.
그래서 OBB도 지금 소개할 대상에서는 제외합니다. 얘도 비싸요.
정점 배열로부터 구체 바운딩 볼륨과 AABB(Aixs Align Bounding Box)생성
뭔가 도형으로 돌아오니 살맛이 나네요.
구체 바운딩 볼룸(Sphere Bounding Voulme)
질량중심좌표를 사용하면 물리처리할땐 좋겠지만, 여기선 필요없습니다. 아주 심플하죠.
- CenterPoint : Vector - 정점배열의 평균값으로 구합니다
- Radius : float - 정점배열의 평균값에서 가장 멀리 있는 정점과의 변위입니다.
AABB(Aixs Align Bounding Box)
얘는..Rect를 다뤄봤다면 별거 아닙니다.
- MinPoint : Vector - 정점배열중 가장 작은 각각의 x,y,z 값의 합성
- MaxPoint : Vector - 정점배열중 가장 큰 각각의 x,y,z 값의 합성
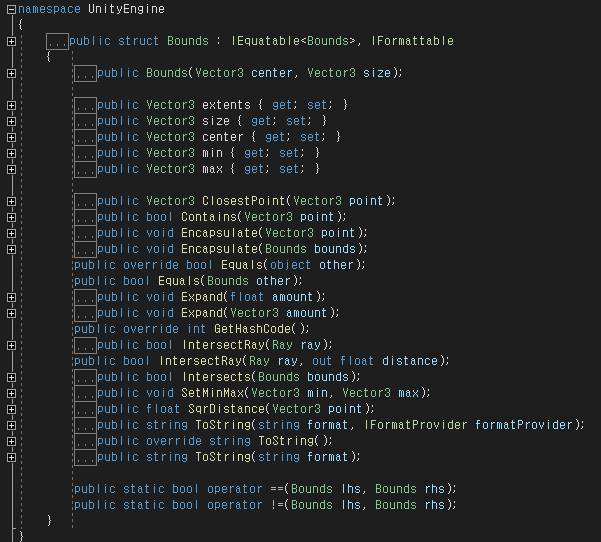
대신 AABB는 Center와 Size, Expant 등으로 표현하기도 합니다.
![Untitled]()
무엇을 쓰든 그것은… 자유입니다.
개인적으론 생성할 때는 min+max가 편하고, 조절할땐 center+extents가 편합니다.
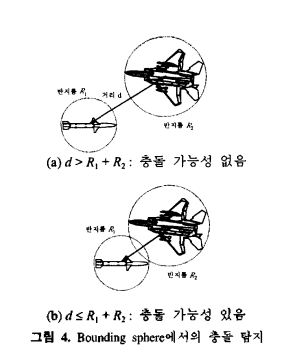
구체바운딩볼륨과 평면의 테스트를 진행시 외부와 접(intersect)의 조건
원의 방정식을 그대로 적용하면 됩니다.
…아니 그냥 거리비교하면 됩니다. 뭐 별거 있나요?
1
2
3
4
5
6
7
8
9
10
11
12
13
| //평면의 방정식에서 거리구하는건 죽어라 했으니 대충 함수가 있다고 가정하겠습니다.
//타입은 유니티!
bool Intersects(in Plane plane, in Sphere sphere)
{
//plane.GetDistanceToPoint은 부호있는 거리를 반환합니다.
return Mathf.Abs(plane.GetDistanceToPoint(sphere.center)) <= sphere.radius;
}
bool Outside(in Plane plane, in Sphere sphere)
{
//plane.GetDistanceToPoint은 부호있는 거리를 반환합니다.
return plane.GetDistanceToPoint(sphere.center) > sphere.radius;
}
|
사실 GetSide함수를 통해 하나로 깔끔하게 정리할 수 있지만…
저희는 이해를 위한 코드를 적으니까요? (헉 근데 이거 html로 변환 되나?)
AABB 바운딩 볼륨과 평면의 테스트를 진행시 외부와 접(intersect)의 조건
이친구는 개념자체는 쉽습니다.
- 단순히 가장 가까운 점부터 평면까지의 거리가 0보다 크다면 외부,
- 가장 가까운 점부터 평면까지의 거리가 0보다 작거나같으며 동시에 가장 먼 점의 거리가 0보다 크거나 같다면 접합니다.
하지만 코드로 짜는게 어렵죠.
두가지방법이 있습니다. 수학적으로 처리하거나, 8개의 점을 통해 처리하거나.
1
2
3
4
5
6
7
8
9
10
11
12
13
| bool Intersects(in Plane plane, in Bounds b)
{
Vector3 center = (b.max + b.min) * 0.5f; //center
Vector3 extent = b.max - center; *//*extents
float r = extent.x * Mathf.Abs(plane.normal.x)
+ extent.y * Mathf.Abs(plane.normal.y)
+ extent.z * Mathf.Abs(plane.normal.z);
float s = Vectpr3.Dot(plane.normal, center ) - plane.distance;
return Abs(s) <= r;
}
|
(대충 토하는 이모티콘)
로컬 공간에서 절두체 컬링을 구현하는 방법을 정리
로컬 공간 → 클립 공간 변환
Vclip=PVM⋅Vlocal행렬은 결합법칙과 분배법칙이 성립하므로
Vclip=P⋅Vview=PVM⋅Vlocal=(PVM)⋅Vlocallet PVM=FProwi 대신에 Frowi 로 대체
−(Frow4+Frow1)⋅ v≤0−(Frow4−Frow1)⋅ v≤0−(Frow4+Frow2)⋅ v≤0−(Frow4−Frow2)⋅ v≤0−(Frow4+Frow3)⋅ v≤0−(Frow4−Frow3)⋅ v≤0나머진 다시 위랑 똑같습니다.
어짜피 계산은 컴퓨터가 돌려주니까요….
끝내며
힘들어요.
[참조 1 - 충돌탐지방법들의 소개 : 백낙훈]
[참조 2 - BoundingSphere : unity doc]
[참조 3 - Bounds : unity doc]