벡터의 내적

벡터 내적연산의 성질 및 공식

유도 및 정리

교환(1) 결합(2) 분배(3)

9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled.png

따라서,

곱셈의 교환법칙이 성립하므로, 내적의 교환법칙 역시 성립한다.
두 식이 같지 않으므로, 내적의 결합법칙은 성립하지 않는다.
덧셈의 교환법칙이 성립하므로, 내적의 분배법칙은 성립한다.

코사인

9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%201.png

\therefore v \cdot u = ||v|| ||u|| cos \theta

만약, 정규화된(normalized) 벡터라면 노름이 1이므로

v \cdot u = cos \theta

이와 같은 공식이 나옵니다.

정규화(Normalize)

  
void Normalize(this Vector2 vector)
{
	  var norm = sqrt(vector.x * vector.x + vector.y * vector.y)
	  vector.x /= norm;
	  vector.y /= norm;
}

투영

9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%202.png

\therefore u_p = \frac{(u \cdot v) \cdot v}{||v||^2} = \frac{(u \cdot v) \cdot v}{v \cdot v}\\ if(||v|| = 1) ,\space then \space u_p = (u \cdot v) \cdot v

그리고 유니티 엔진에서 코드를 뜯어왔습니다.

  
//in UnityEngine/Runtime/Export/Math/Vector3.cs
Vector3 Project(Vector3 vector, Vector3 onNormal)
{
    float sqrMag = Dot(onNormal, onNormal); // ||v||^2
    if (sqrMag < Mathf.Epsilon)
        return zero;

    var dot = Dot(vector, onNormal);
    return new Vector3(onNormal.x * dot / sqrMag,
        onNormal.y * dot / sqrMag,
        onNormal.z * dot / sqrMag);
}

어때요 참 쉽죠?

벡터 내적의 응용

시야각 범위내의 물체 판별

시야각 범위 내의 물체 판별을 어떻게하면 좋을까요?

바라보는 정면에서부터의 각도를 사용해서 각이 더 작으면 시야각 안에 들어있다고요?

그것도 맞기는 합니다. 하지만 각을 구하기 위한 atan은 너무나도 비쌉니다.

정답은 당연히 『내적(Dot product)』입니다.

정답은 당연하게 놔두고 어떻게 사용할 지에 대해서 생각해 봅시다.

코사인 유사도 (Cosine Similarity)

이것 참… 최근(?)에 짠 코드를 리뷰하게 될 줄은 몰랐습니다.

최근 ‘정확한 백어택’ 공격에 대한 점수 판정을 작성할 일이 있어, 코드를 조금만 인용해왔습니다.

  
//충돌시 피격자
info.hitAngle = Vector3.Dot(velocity.normalized, transform.forward);
info.hitVelocity = velocity;
info.hitDistance = transform.InverseTransformPoint(otherPosition).ToXZ().magnitude;

//점수 판정부
...

if (info.hitAngle < 0.90631f) //25 degree , cos(25 * pi/180) baked
    return defaultScore + additionalScore;

...

return Mathf.Clamp01(defaultScore + additionalScore + hitAngleScore + speedScore + distanceScore);

필요로 하는 것은 충돌대상의 정면방향과 공격의 진행방향의 유사도 입니다.

이를 코사인, 즉 내적을 사용해서 쉽게 얻을 수 있는데 이걸 진행하기 전에 생각할 것이 있습니다.

일단 두 벡터의 내적관계에 대한 간단한 그림을 그려봅시다.

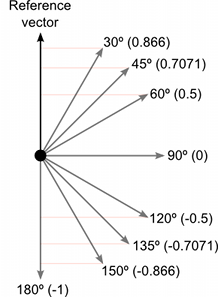
Untitled%204.png

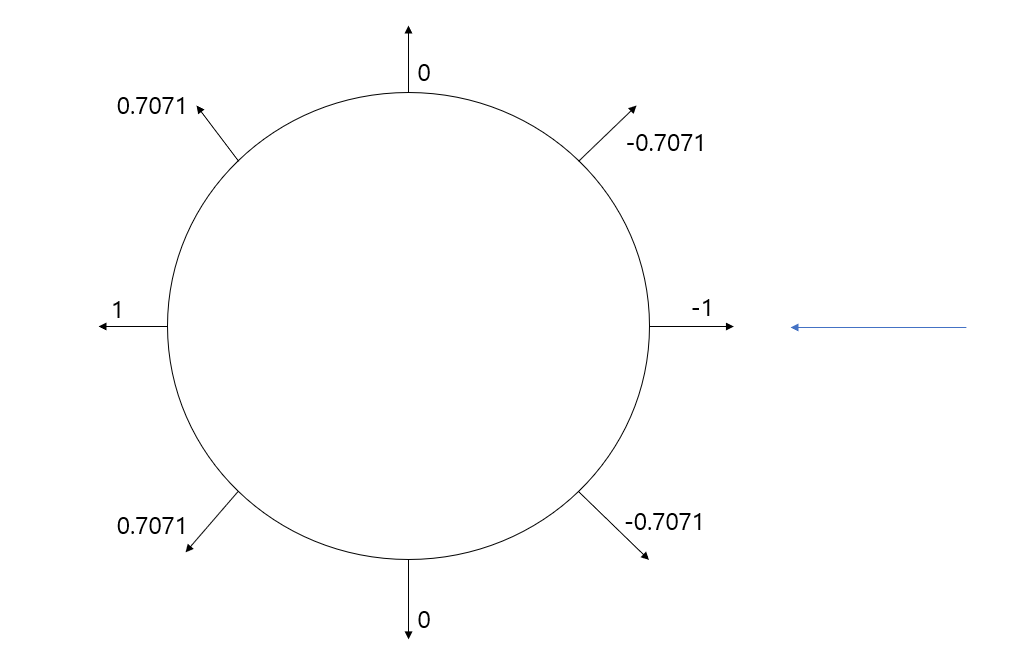
9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%203.png

다음과 같이 두 그림을 보면

같은방향일때 1, 정 반대의 경우 -1까지의 값에 대응합니다. 선형적이지 않지만, 접선의 기울기의 부호가 특정 범위에서 일정하는 것을 알 수 있죠.

따라서, 비교가 간단하게 대응이 가능합니다.

시야각이 고정적일 경우 - 미리 구워둔 값과 비교

시야각의 경우, $\theta$ degree라고 가정할 때, $cos(\frac{\theta}{2})$ 값을 미리 구워둡니다.
그리고 물체의 위치(점) 에서 시야의 위치(점)을 뺀 벡터를 구합니다.
시야의 정면 벡터와 해당 벡터를 내적한 값을 구합니다.
구워둔 시야각의 값과 3.에서 내적한 벡터의 값의 차이를 통해 내부와 외부를 판별합니다.

예를 들어 시야각 60도 일 경우, 30에 해당하는 0.866이 구워진 값이며,

시야정면벡터와, 오브젝트와 시야의 변위벡터의 내적을 통해 0.866 보다 크다면 시야에 포함,

0.866보다 작다면 시야에 포함되지 않음 입니다.

…엇 설마 처음 구워둔 상수값을 구하는 것도 내적이 아닌 방법이라 감점인가요?

시야각이 유동적일 경우 - 시야각에 해당되는 벡터와 비교

시야각의 경우, $\theta$ degree라고 가정할 때 해당 값만큼 정면 시야를 회전한 벡터를 하나 만듭니다.
그리고 물체의 위치(점) 에서 시야의 위치(점)을 뺀 벡터를 구합니다.
시야의 정면 벡터와 해당 벡터를 내적한 값을 구합니다.
시야 정면 벡터와 최대 시야 벡터를 내적한 값을 구합니다.
4.에서 내적한 벡터의 값과 3.에서 내적한 벡터의 값의 차이를 통해 내부와 외부를 판별합니다.

코사인 유사도는 이런 사항 뿐만 아닌 데이터마이닝 등에서 데이터 응집도 검사, 문서 유사도 검사에서도 사용됩니다. 물론 그전에 NLP(자연언어처리)의 변환처리인 BoW, DTM, TF-IDF나 Text Vectorization등을 거친 이후에 사용되겠지만요. 하하

직교행렬

2x2 직교행렬과 이 행렬의 전치행렬의 곱은 항등행렬임을 증명

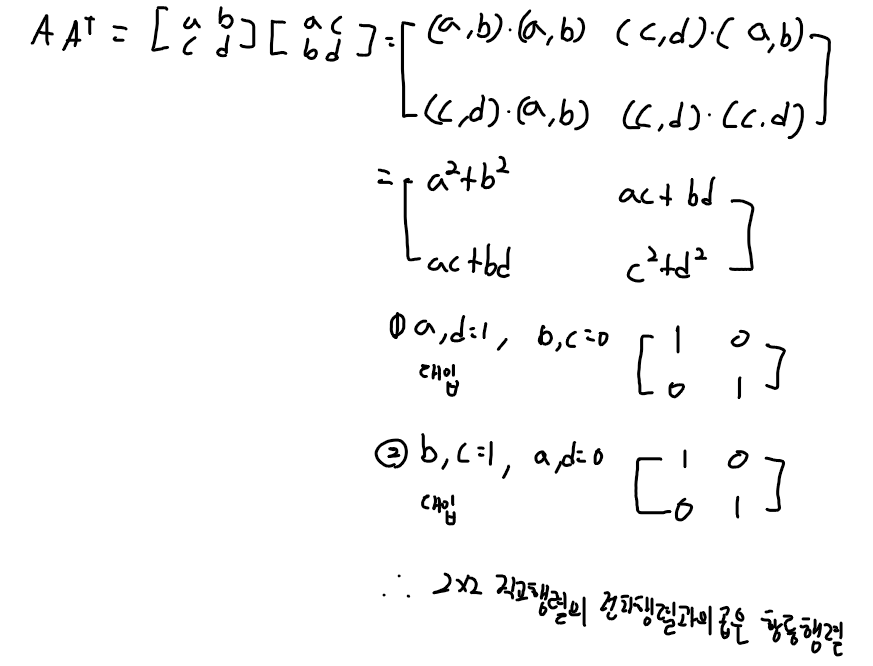
9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%204.png

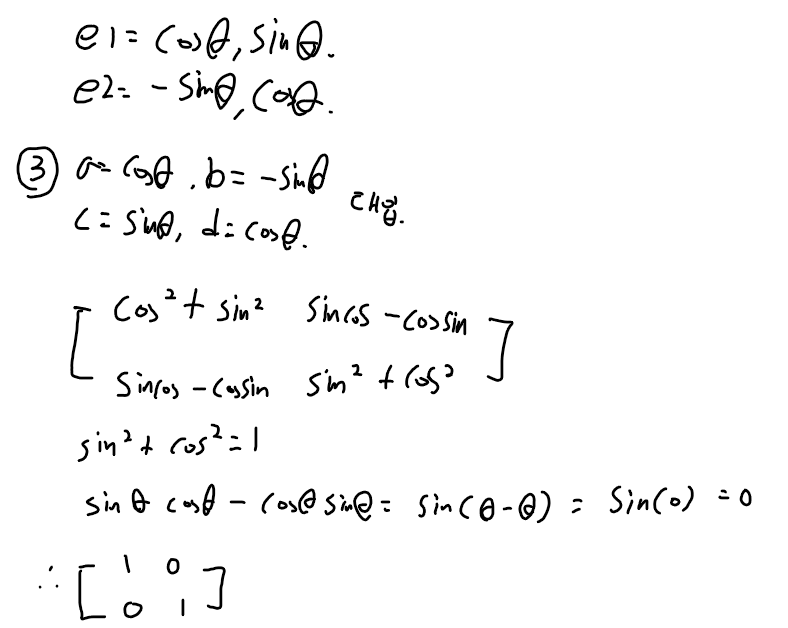
9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%205.png

따라서, 2x2 직교행렬과 이 행렬의 전치행렬의 곱은 항등행렬입니다

회전행렬은 직교행렬인가

직교행렬의 정의부터 확인해보겠습니다.

9%20Vector%20Dot%20Product%20fc910f4dcff0497594d43bd6c675173d/Untitled%206.png

위에서 2x2 직교행렬과 이 행렬의 전치행렬의 곱은 항등행렬이라고 하였습니다.

그러면 두 행렬의 곱이 항등행렬이 나온다면, 이 행렬은 직교행렬일까요?

두 행렬의 곱이 항등행렬일때, 두 행렬은 서로 역행렬입니다.

그리고 전치하였을 때 역행렬이 나오는 경우, 더 따져봐야겠지만 일단 가장 큰 조건을 만족하므로 를 직교행렬이 될 가능성이 높다고 봐야겠죠.

자 그러면 두 행렬( $\bold{AA^T}$ )의 곱이 항등행렬이 나온다면, 이 행렬은 직교행렬이라고 봅시다.

그리고 어쩌다보니 회전행렬과 그 행렬의 전치행렬의 곱이 항등행렬임은 이미 증명한 것 같습니다..

\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}

라는 회전 행렬에 대해서,

\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} cos(\theta) & sin(\theta) \\ -sin(\theta)& cos(\theta) \end{bmatrix} \\

를 수행하여 봅시다.

\bold{AA^T} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} a^2 + b^2& ac+bd\\ ac+bd & c^2+d^2 \end{bmatrix}

임을 생각하여,

a = cos(\theta),\space b = -sin(\theta)\\ c= sin(\theta),\space d = cos(\theta)

를 대입하여 봅시다.

\bold{AA^T} = \begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} cos(\theta) & sin(\theta) \\ -sin(\theta)& cos(\theta) \end{bmatrix} \\ = \begin{bmatrix} cos^2 + sin^2 & sincos-cossin\\ sincos-cossin & sin^2+cos^2 \end{bmatrix}

여기서 다시

cos^2 + sin^2 = 1\\ sin(\theta)cos(\theta) - cos(\theta)sin(\theta) = sin((\theta)-(\theta)) = sin(0) = 0

의 식을 사용하여 대입하게 된다면,

\bold{AA^T} = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}

의 항등행렬이 나타나게 됩니다.

따라서 회전행렬은 직교행렬이라고 생각합니다

회전행렬의 전치행렬은 어떤 변환을 의미하는가

회전행렬의 전치행렬….?

회전행렬이 직교행렬임이 증명되었기 때문에, 전치행렬은 역행렬이라 생각할 수 있고,

역행렬의 의미상 이는 반대로 대응되는 관계라 볼 수 있습니다.

그리고 이를 행렬로 둬서 기저벡터의 단위로 생각하게 된다면,

\begin{bmatrix} cos(\theta) & sin(\theta) \\ -sin(\theta) & cos(\theta) \end{bmatrix}

기존 $\theta$ 값이 증가함에 따라 모든 기저벡터는 ‘반시계방향’으로 회전했습니다.

다만 전치행렬을 유심히 읽어보면 $\theta$ 값이 증가함에 따라 ‘시계방향’으로 회전한다는 것을 알 수 있습니다.

즉 회전행렬의 전치행렬은 회전 방향의 변환을 의미하게 됩니다.

회전이 특정 축을 기준으로 하게된다면, 해당 축이 반대로 된다고 볼 수 있습니다.

2차원의 경우 2차원에 직교인 가상의 축이 반대로 된 경우의 회전을 수행한다 볼 수 있다고 생각합니다.

8. 벡터의 내적