저번주차 과제부터 실험적으로 노션에 작성한 게시글을 github.io에 옮기고 있습니다.

그런데 이게 좀 문제가 많더라고요. 인용도 날라가고 인라인 수학도 날라가고

katex도 지원하지않아 플러그인을 추가하고 이미지링크도 날라가서 수정해야하고…

몇시간에 걸쳐 설정하였지만 나름 재미있던 방법인 것 같습니다.

(그래도 티스토리나 wix같은게 더 편할 것 같아요)

노션에서 제공하는 기능은 추출하기 불편합니다.

아무튼 이런저런 이유때문에 이번주차부터는 조금 더 담백하게 작성될 것 같습니다.

그러면 이번주차의 게시글, 시작합니다.

평면의 방정식

평면의 방정식이란 무엇일까요? 저희는 2차원 직교 좌표계에서 직선의 방정식을 다루어보았습니다.

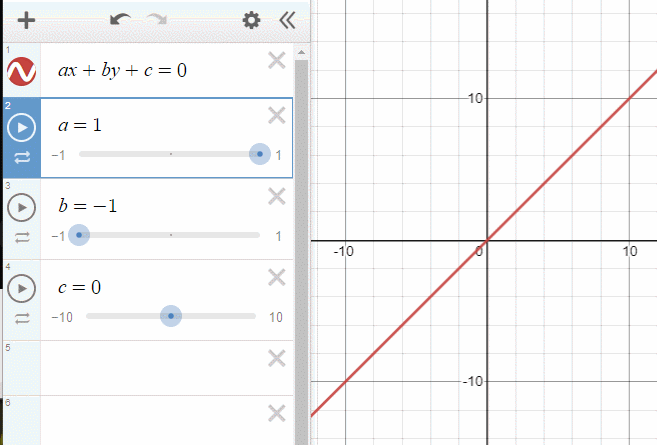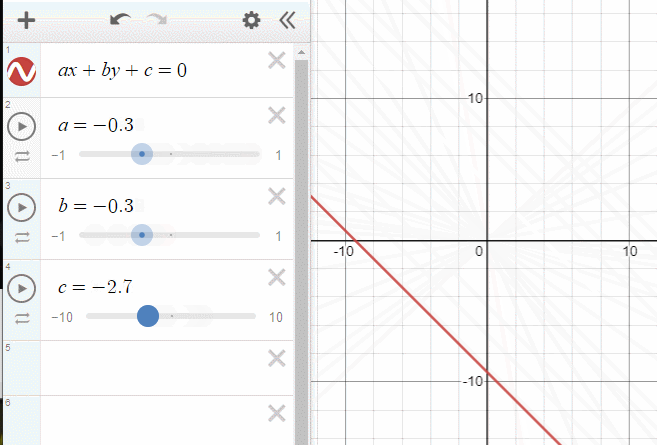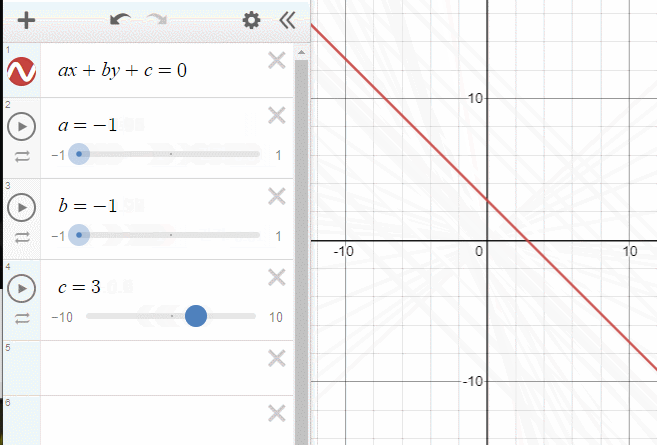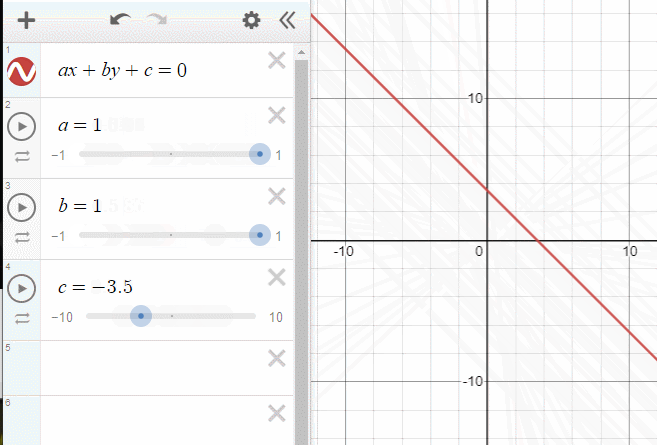
Untitled

그 개념을 3차원으로 확장하였다고 보아도 무방하죠.

이번에는 순수 수학에 가깝습니다. 저와같은 수포자에게는 꽤나 어려운 주제지만 한번가봅시다.

평면을 표현하는 방법부터 갑시다.

평면은 생각을 하자면 면 하나, 즉 점들의 집합의 집합 입니다.

두 점으로 선을 만들 수 있으니 세 점으로 면을 만들 수 있겠죠.

두 점의 변위벡터 두개로 공간을 형성할 수 있으니까요.

이를 벡터방정식 이라고 합니다

하지만 다른 관점도 존재합니다. 면이 보는 방향, 면이 속해있는 점.

면이 보는 방향은 노멀이고, 이 노멀은 면에 대해 직교(외적의 그것이요)하므로, 공통된 정보를 가질 수 있죠. 이는 point-normal 방정식(form)이라고 합니다

다른방식으로는 매개방정식이라는 것이 존재하지만.. 이것은 언급만 하고 넘어가도록 하겠습니다.

결국 다 똑같은 것이니까요.

저희가 이번에 다뤄볼 것은 Point-Normal 방정식의 방법입니다.

그러면 유도식부터 시작해볼까요?

평면의 방정식 유도

평면의 방정식을 Point-Normal 관점에서 본다면 간단합니다.

바로 어떤 지점과 평면이 속한 점의 변위벡터와 노멀을 내적했을때 0일 경우 수직이다. 입니다

내적은 cos, 즉 각도가 90도 일때 0이 나오기 때문이죠.

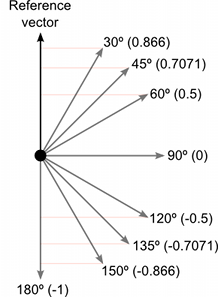
Untitled

즉 해당 내용을 식으로 본다면

\hat n \cdot (r - r_0) = 0\\\space \\ let \space \hat n = (a,b,c) ,\space r = (x,y,z),\space r_0=(x_0,y_0,z_0)\\ a(x-x_0)+b(y-y_0)+c(z-z_0) = 0

으로 볼 수 있으며

이를 전개해서 묶는다면

ax-ax_0+by-by_0+cz-cz_0 = 0\\ ax+by+cy - (ax_0+by_0+cz_0) = 0

로 둘 수 있습니다.

이제 여기서 $- (ax_0+by_0+cz_0)$ 는 $r_0$ 와 $\hat n$ 으로 조립할 수 있으니 $d$ 로 설정합니다.

ax+by+cy - (ax_0+by_0+cz_0) = 0\\ ax+by+cy + d= 0

어때요 참 쉽죠?

평면의 방정식에서 d란?

이제 잡다한것 다 빼고 d만 살펴봅시다.

대신 지금 계산할 때에는 normal이 단위벡터라는 가정하에 진행합니다.

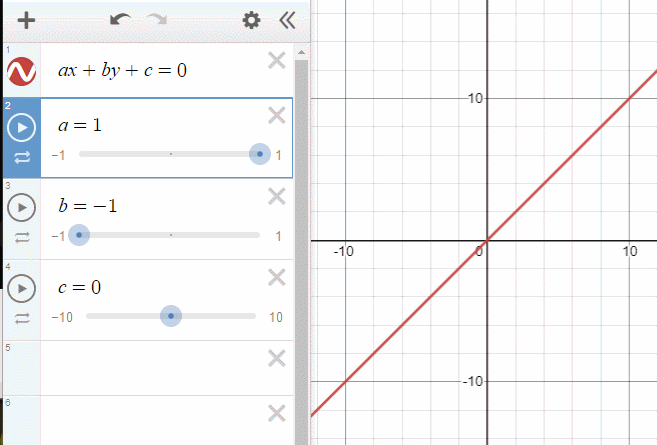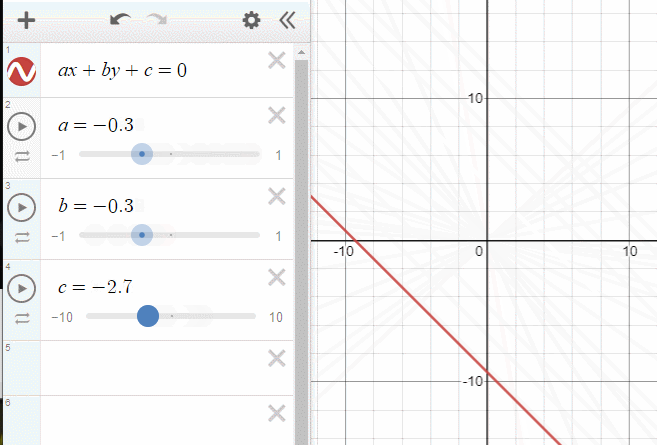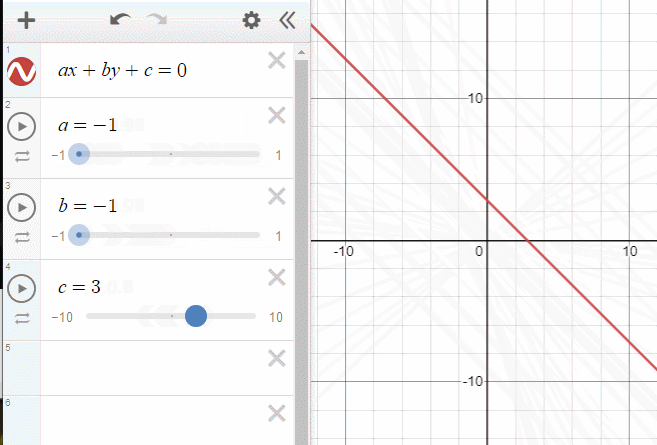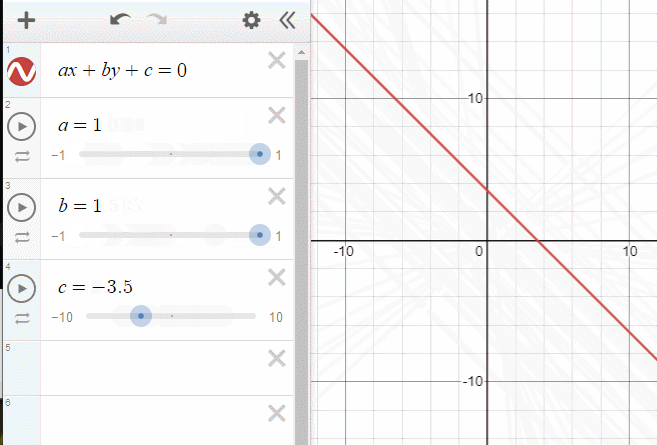
Untitled

아까 위에서 보여준 그래프(직선의 방정식)에서 c를 조절하면 원점으로 부터의 거리가 바뀌었습니다. 평면의 방정식은 직선의 방정식의 차원을 한단계 늘렸을 뿐이므로, 단순하게 생각하면 d의 값은 똑같은 역할을 하게 됩니다.

식의 값으로 본다면

ax_0+by_0+cz_0= \hat n \cdot r_0 \\ \therefore -(ax_0+by_0+cz_0)= -\hat n \cdot r_0

로 볼 수 있겠네요.

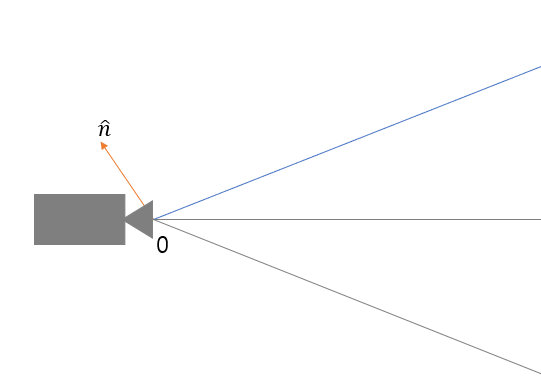
시각화해봅시다.

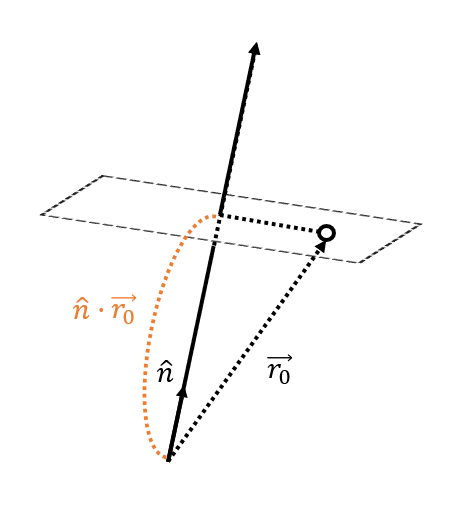
Untitled

즉 결국 저것만 떼서 보면 위 그림과 같은 꼴이 나오는겁니다.

일단 두 벡터를 내적한 값의 부호를 생각해본다면

Untitled

d=-|\hat n|\cdot|\vec{P_0}|cos\theta\\

따라서 두 벡터를 내적한 값이 0보다 크다면 원래는 같은 방향이라는 뜻일테지만, -1이 곱해져 이므로 반대로 생각하면 됩니다.

그리고 저 벡터의 크기는 원점에서 평면까지의 거리라고 볼 수 있죠.

정리해보자면

부호(Sign) : 면과 같은방향(d < 0), 면과 반대방향 (d > 0)
크기 : 원점에서 평면까지의 최단거리(직교함)

입니다.

점의 위치 : 평면의 외부 혹은 내부 판별

일단 평면의 외부와 내부는 평면과 원점의 사이, 혹은 평면에서 원점으로 향하는 벡터의 스칼라배를 통해 얻을 수 있는 점을 ‘내부’라고 칭하겠습니다.

아까 위에서 크기는 원점에서 평면까지의 최단거리라고 하였죠?

그런데 r은 특정 지점이였기 때문에 둘다 노말에 투영하면 쉽게 알 수 있습니다.

간단하게 보자면 임의의 점이 내부에 있는 경우입니다.

\hat n \cdot r < \hat n \cdot r_0 \\ ax+by+cz < ax_0+by_0+cz_0\\

식을 쭉 풀어보면 다음과 같은 꼴이 되죠

ax+by+cz < -(-( ax_0+by_0+cz_0))\\ ax+by+cz < -d\\ ax+by+cz+d < 0

otherwise, 외부입니다.

점과 평면의 최단거리

일단 최단거리이므로, 수직일 것입니다. 그러면 법선과 내적해야겠죠?

그러면 법선벡터와 점에서 그은 평면위로 향하는 변위벡터와 내적합니다.

방향이 반대라도 어짜피 거리라 절댓값을 취하니 패스하고,

그 값을 법선벡터의 길이로 나누면 되겠네요.

뭔소리냐고요?

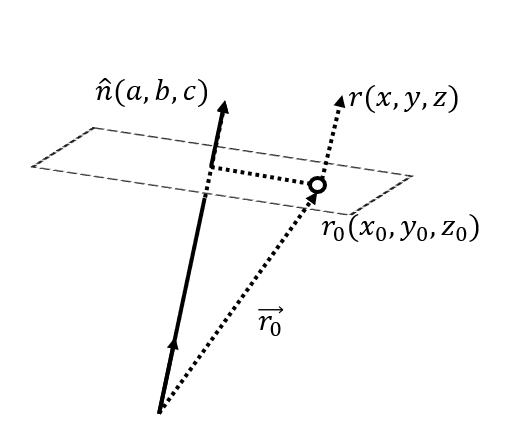
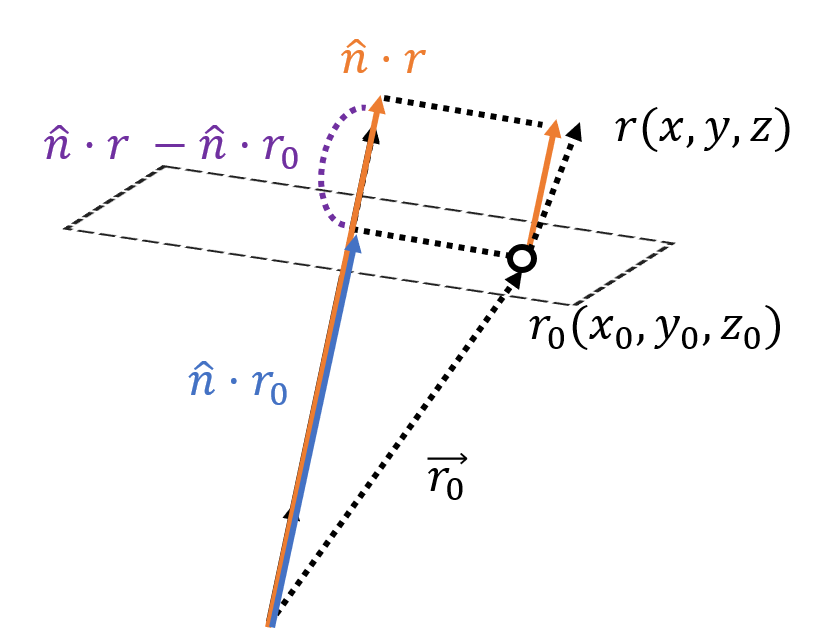
Untitled

D = \frac{|ax+by+cz+d|}{\sqrt{a^2+b^2+c^2}}

어짜피 원점에서부터의 거리나 특정점에서부터의 거리나,

벡터를 구해서 처리한다는 부분은 똑같기때문에, 그냥 처리하면 됩니다.

어라 그런데 분모가 있네요?

평면의 방정식 정규화

이건 어쩌다보니 같이 처리하게 되었는데,

ax+by+cz+d = 0

이때 d의 값에 따라 오프셋이 조절되게 되는데,

노멀벡터의 크기로 나누게 되면 정규화된 값을 얻을 수 있습니다.

쉽게 알아볼 수 있도록 직선의 방정식을 이용해서 표현해보았습니다.

ax+by+cz+d = 0\\ ax+by+cz+0 = -d

에 따라 직선의 방정식의 c를 사용하지 않고 d를 두었습니다.

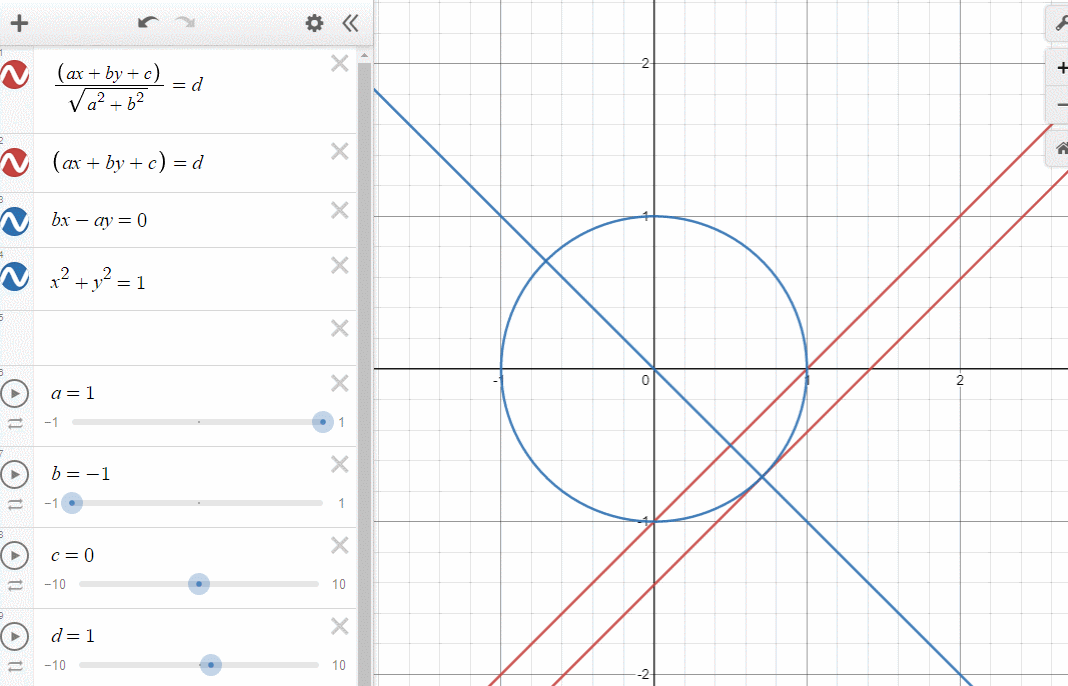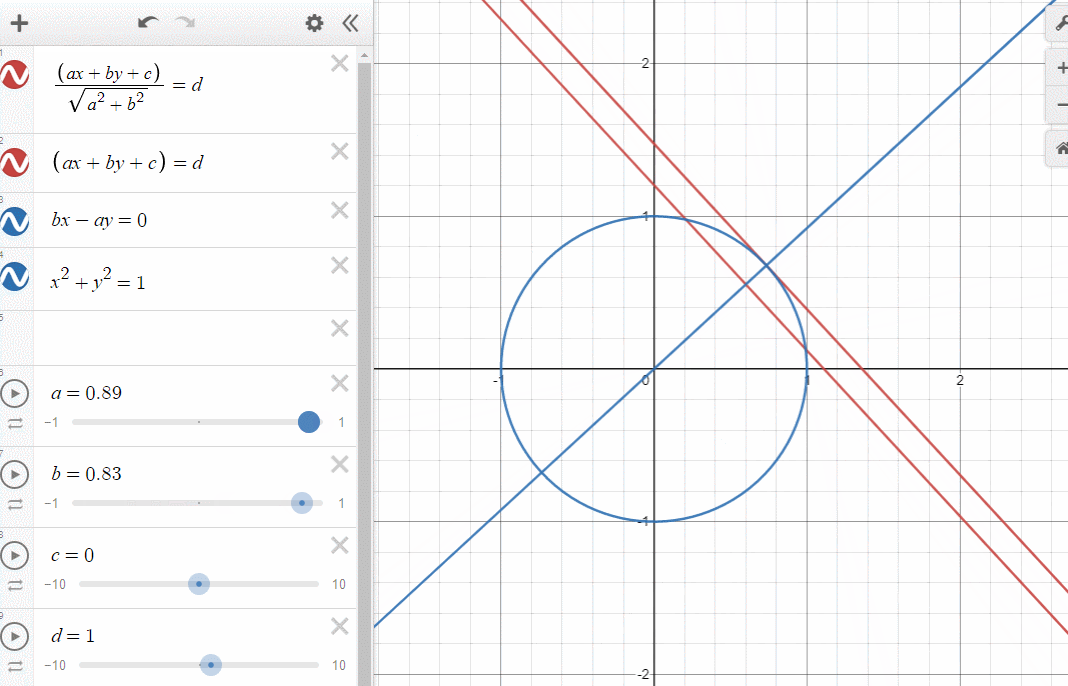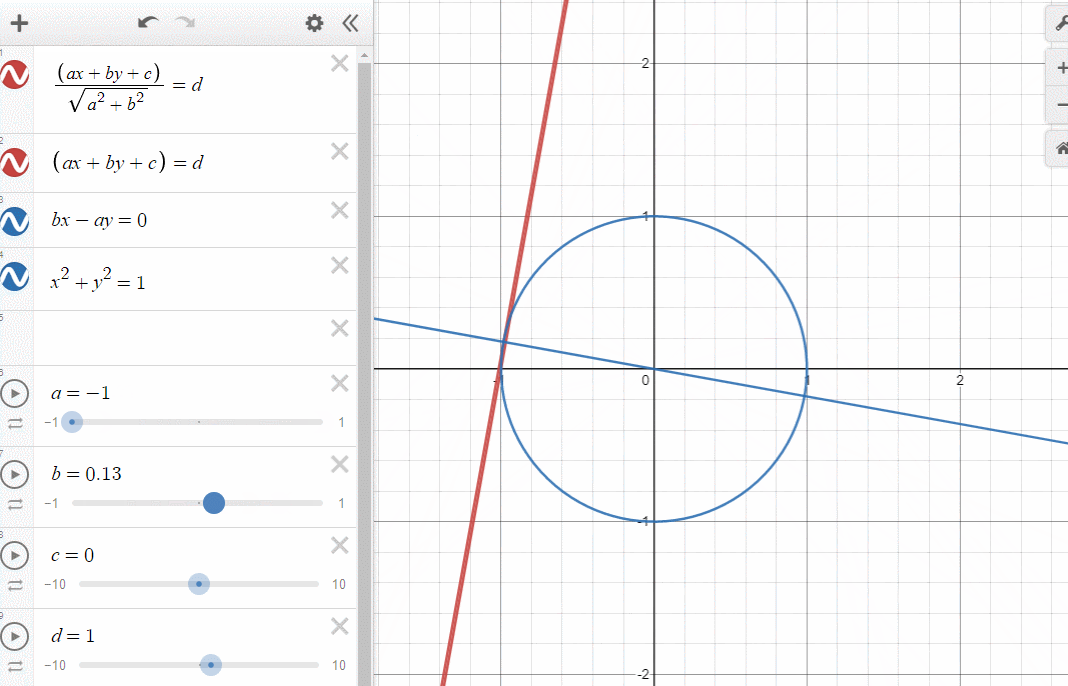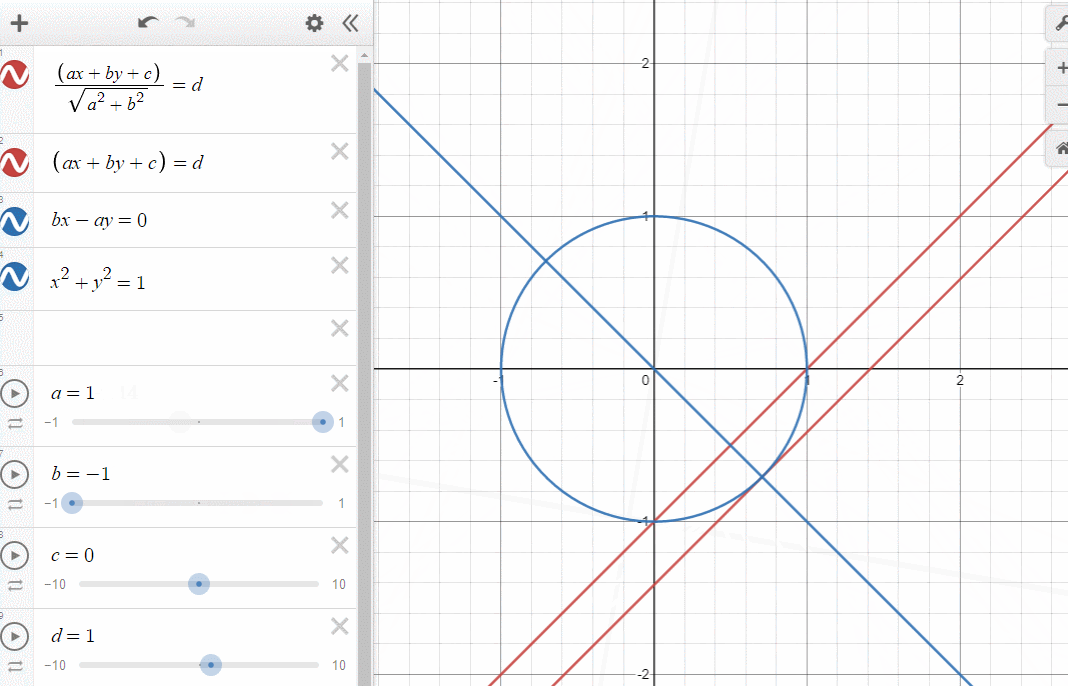
Untitled

그러면 뭐다?

\frac{ax+by+cz+d}{\sqrt{a^2+b^2+c^2}} \\ =\frac{ax+by+cz+d}{|\vec{n}|}\\ =0

아까봤던 분모의 이유가 저것입니다.

어짜피 단위벡터라면 1이라서 계산하지 않지만 명시적으로 적어뒀을 뿐입니다.

절두체

절두체란 무엇인가 .

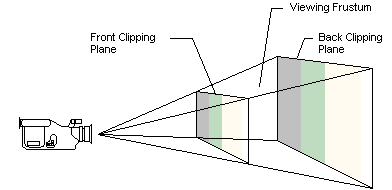
Untitled

카메라가 보고있는 장면의 3D볼륨,퍼스펙티브 관점에서 피라미드처럼 구성된 입체라고 생각하면 됩니다.

즉 실제 렌더링되는 영역이라는 것이죠.

절두체를 구성하는 6개의 평면의 방정식

Untitled

일단 3차원을 2차원이라고 생각한다면 y에 대한 식과 x에 대한 식은 유사합니다.

따라서 z를 분리해서 고려하고, 나머지는 각 평면에서 바라볼 때,

평면의 점을 0벡터라고 가정하여 노말벡터와 내적하면 d = 0이므로 d소거,

yz평면에서의 x는 사라지는 꼴을 띄므로 하나의 성분이 사라집니다.

그러면 뭐 이제 삼각함수써서 뚝딱하면 됩니다.

Z_{near}\rightarrow z+near=0\\Z_{far}\rightarrow -z-far=0\\\space \\ Y_{up} \rightarrow (sin(\frac{\pi}{2} - \frac{\theta}{2}))y+(cos(\frac{\pi}{2} - \frac{\theta}{2}))z=(cos\frac{\theta}{2})y+(sin\frac{\theta}{2})z=0\\Y_{down}\rightarrow(-sin(\frac{\pi}{2} - \frac{\theta}{2}))y+(cos(\frac{\pi}{2} - \frac{\theta}{2}))z=(-cos\frac{\theta}{2})y+(sin\frac{\theta}{2})z=0\\\space \\ X_{left}\rightarrow(-sin(\frac{\pi}{2} - \frac{\theta}{2}))x+(cos(\frac{\pi}{2} - \frac{\theta}{2}))z=(-cos\frac{\theta}{2})x+(sin\frac{\theta}{2})z=0\\X_{right}\rightarrow(sin(\frac{\pi}{2} - \frac{\theta}{2}))x+(cos(\frac{\pi}{2} - \frac{\theta}{2}))z=(cos\frac{\theta}{2})x+(sin\frac{\theta}{2})z=0\\

짠

두 평면의 방정식 n+f=0과 -n-f=0의 차이에 대해 설명하시오.

어라…n+f = 0 과 -n-f=0의 차이…?

음…비슷한식이 z+near = 0 과 -z-far=0밖에 없어 이걸로 이해하고 작업하겠습니다.

결론적으로 거리에 따라 면의 내부와 외부를 결정해야하는데,

면의 노말이 다르기 때문에 발생합니다.

그래서 두개를 0으로 만들기 위해 맞춰주는 것이죠.

어떤 점이 절두체 안쪽에 있는지 판별하는 방법을 순서도로 설명하시오.

그냥 한번이라도 노멀과 내적한 값이 0보다 크다면 면의 밖에 존재하기때문에 전부 거르고,

원평면과 근평면은 이제 거리값에 따라 조절해주면 됩니다.

Left,Right,Up,Down,Near,Far 의 순서로 진행하였습니다. (L,R,U,D,near,far)

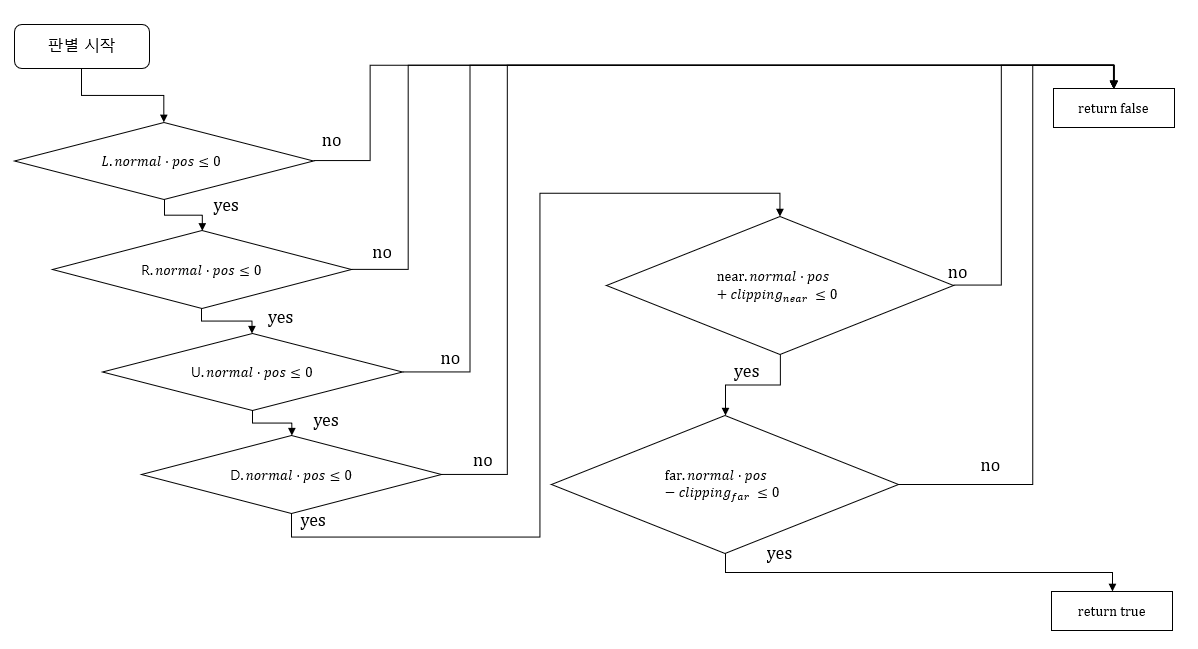
Untitled

아 이거 맛깔나게 그리기가 힘드네요.

다음부터는 따로 도구를 써야겠습니다.

실습 예제의 문제점 두 가지를 설명하시오.

종횡비를 고려한 상하 평면이 구성되지 않았다
오브젝트의 바운더리를 처리하지 않았다.

종횡비는 NDC때 한번 다뤄봤으니 패스하고,

… 이게 사실은 바운더리하면 또 생각나는 이야기가 있습니다.

예전에 Planar Shadow를 사용한 적이 있는데, PlanarShadow는 버텍스 정점을 평면에 투영하기 때문에 실제 버텍스의 위치와 달라지게 됩니다.

그런데 이게 이제 카메라의 끝에 가서 실제 렌더링이 안되는 영역에 넘어간다면, 그림자도 안그려지게 되는 것 이죠.

이것이 바운더리 문제입니다.

해결방법은 mesh의 bound를 설정하거나 skinned Mesh의 경우 SkinnedMeshRenderer.localBounds를 수정하는 방법이 있습니다.

이를 위한 방법들은… 다음주에 설명하게 될 것 같네요.

향상 과제

내적 연산을 ‘스칼라 곱’이라고도 표현한다. 내적 연산은 어떤 작업을 하는 연산인지 자신의 생각을 자유롭게 정리하시오.

저는 내적 연산에 대해 공통적으로 0이 나오면 직교한다고 생각합니다.

그 케이스가 아니라면 세가지로 보는데,

바로 정규화된 벡터냐 아니냐에 따른 분류입니다.

정규화된 두 벡터
정규화된 벡터간의 내적은 내적 = 코사인 = 유사도 라고 생각합니다.
시초는 N dot L, 노멀과 빛의 내적을 통한 쉐이딩이였습니다.
정규화된 벡터와 아닌 벡터
이 경우는 투영입니다. 어떤 벡터를 정규화된 벡터와 내적하는건 투영이죠.
크기가 제 각각인 벡터
이경우는 두 벡터의 유사도와 크기를 곱한 값입니다.
자기자신으로 내적한다면 sqrMagnitude와 같으며, 단순 벡터간의 크기 대소 비교를 ‘조금 더 싸게’ 검사할 때 사용합니다.
솔직히 이 경우를 제외하고는 모르겠습니다.

아무튼 솔직히 개인적인 생각으로

‘내적연산은 어떤연산이다!’ 가 아니라 ‘이런연산을 할 때 내적연산을 한다!’ 로 씁니다.

유사도를 비교하면 내적, 투영할때 내적, 단순 벡터 크기 비교할때 내적.

마치며

또다시 일주일이 지났지만 점점 지쳐갑니다.

참조

Equations of planes

6. Frustum

평면의 방정식

평면의 방정식 유도

평면의 방정식에서 d란?

점의 위치 : 평면의 외부 혹은 내부 판별

점과 평면의 최단거리

평면의 방정식 정규화

절두체

절두체를 구성하는 6개의 평면의 방정식

두 평면의 방정식 n+f=0과 -n-f=0의 차이에 대해 설명하시오.

어떤 점이 절두체 안쪽에 있는지 판별하는 방법을 순서도로 설명하시오.

실습 예제의 문제점 두 가지를 설명하시오.

향상 과제

내적 연산을 ‘스칼라 곱’이라고도 표현한다. 내적 연산은 어떤 작업을 하는 연산인지 자신의 생각을 자유롭게 정리하시오.

마치며

Further Reading

1. 3D Transform

2. Gimbal-Lock & Cross Product

3.Backface Culling & Rodrigues rotation