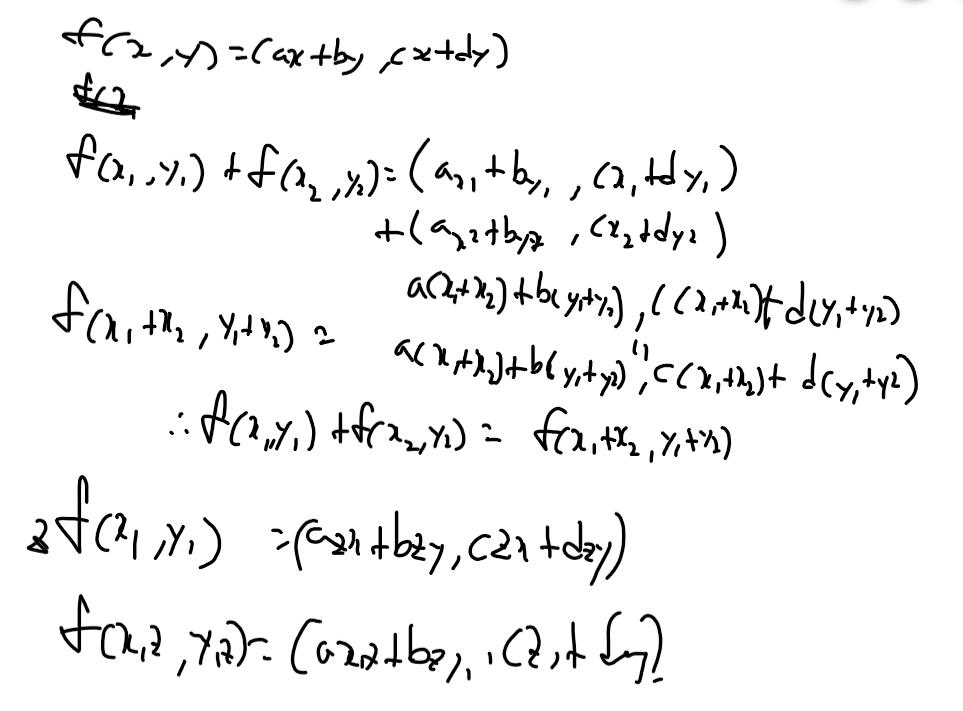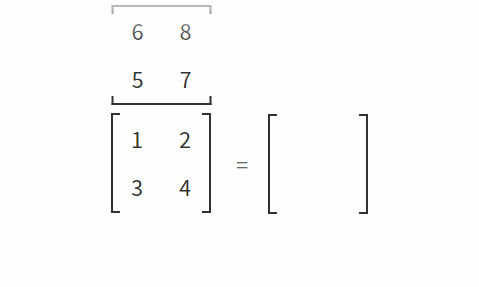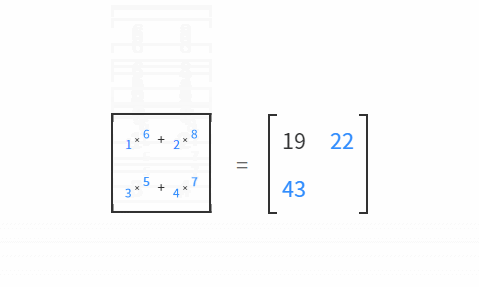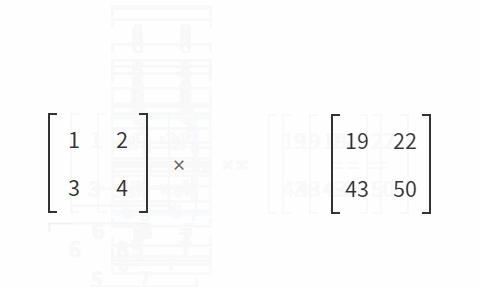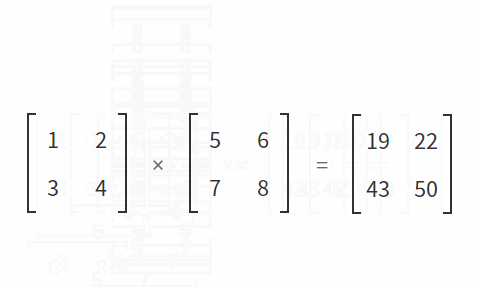5. Linearity, Matrix - multiple | 어쩌다보니 개발자

Polar Coordinate

atan2(y,x) 함수의 인자는 왜 2개일까?

삼각함수의 역함수는 흔히 함수 앞에 arc가 붙게 됩니다.

즉, 특정 각에 대한 특정 비를 사용하는 함수들은, 특정 비율에 대해 특정 각을 나타내는 함수가 되는것이지요.

그 중 아크탄젠트의 경우, 각도에 대한 x와 y의 비율을 가졌기 때문에

역함수가 되며 그 존재가 중요해졌습니다. 벡터공간에서 x와 y 성분을 통해 각도를 구할 수 있게 되었죠.

하지만 문제가 있습니다. 비율이라는 것은 서로 각각 음수와 양수가 포함되기 때문에, 음수 및 음수 혹은 양수 및 양수에서 같은 부호를, 음수 및 양수 혹은 양수 및 음수에서 같은 부호를 반환하게 됩니다.

이렇게 손실되는 정보가 있기 때문에

선행 계산된 값이 아닌 순수한 값 두개를 인자로 받아 내부에서 처리합니다.

내부에서 처리하게 된다면

if x>0
if x<0 && y≥0
if x<0 && y<0
if x = 0 && y ≥0
if x = 0 && y <0

… 이렇게 조건을 타 처리할 수 있겠죠.

수학에서 이야기하는 선형성의 조건

선형성. Linear하다 라고 말할 수 있습니다.

저희는 항상 Linear를 입에 달고 살지만, 정작 이 Linear한 것의 의미를 잘 몰랐다고 생각합니다.

선형적인 것은 보통 나타내면 직선처럼 보이며,

일반적으로 생각했을 때, 예측이 가능하고
프로그래밍 적으로 생각했을 때, interpolate와 extrapolate가 자유롭게 가능한 무언가
수학적으로 생각하였을 때, 미분값이 상수인 것

이라고 생각했습니다.

즉 두 점을 잇는 선분을 상상하며 정보가 주어지면 위치를 예상할 수 있다는 것이죠.

이걸 수학자들은 두가지 특성으로 분리했습니다.

가산성(Additivity) : $f(x+y) = f(x)+f(y)$ $f (x + y) = f (x) + f (y)$
- 더해질때마다 추가적인 무언가가 있으면 안된다 예를 들어 상수 c가 있다면 $y=ax+c$ , 가산성을 만족하지 않습니다
1차 동차성(Homogeneity) : $af(x)=f(ax)$ $a f (x) = f (a x)$
- 정의역과 공역의 공간이 같아야 합니다

함수, 사상, 변환의 차이

함수(Function)의 경우는 집합과 집합의 대응관계
- 가장 기본이 되는 대응관계
사상(Mapping)은 체계를 보존하며 서로 대응하는 관계 (벡터공간→벡터공간)
- 시스템을 유지하기 때문에 연산을 여전히 쓸 수 있습니다
변환(Transformation)
- 벡터에 대한 사상
- 벡터는 선형성을 가지고 있기 때문에, 선형변환(Linear Transformation)이라고 할 수 있습니다.

함수 $f(x,y)=(ax+by, cx+dy)$는 선형성?

두가지 특성, 가산성과 1차 동차성에 대하여 손으로 풀어보았습니다.

5%20Linearity,%20Matrix%20multiple,%20Polar%20Coordinate%2078227d285b464a5390577089f1b1e20d/Untitled.png

적고보니 읽기 힘드니 제대로 수식을 짜봅시다

가산성(Additivity)

f(x,y) = (ax+by,cx+dy)에\space대하여\\ \space\\ f(x_1,y_1)+f(x_2,y_2) = \\ (ax_1+by_1,cx_1+dy_1) + (ax_2+by_2,cx_2+dy_2) = \\ (ax_1+ax_2+by_1+by_2,cx_1+cx_2+dy_1+dy_2)\\\space\\ f(x_1+x_2,y_1+y_2) = a(x_1+x_2)+b(y_1+y_2),c(x_1+x_2)+d(y_1+y_2)= \\ (ax_1+ax_2+by_1+by_2,cx_1+cx_2+dy_1+dy_2) \\\space\\ \therefore f(x_1,y_1)+f(x_2,y_2) = f(x_1+x_2,y_1+y_2)

1차 동차성(Homogeneity)

zf(x,y) = z(ax+by,cx+dy)\\ =(zax+zby,zcx+zdy)\\ f(zx,zy) = (zax+zby,zcx+zdy)\\ \space\\ \therefore f(x_1,y_1)+f(x_2,y_2) = f(x_1+x_2,y_1+y_2)

기본적으로 여기서 $x_1,x_2,y_1,y_2$ 는 모두 체에 속해있다고 가정했습니다.

따라서 덧셈의 교환법칙, 곱셈의 교환법칙, 덧셈과 곱셈의 분배법칙 등을 만족하기때문에,

가산성과 1차 동차성에 대하여 두 값이 동일하기 때문에 선형성을 만족하는 것을 알 수 있습니다.

행렬이란 무엇인가?

수를 1차원적으로 나열한 체계를 벡터라고 하였다면, 수, 문자, 함수등을 네모꼴 괄호 안에 배열하여 2차원 놓은 것이 행렬입니다.

선형변환(Linear Transformation)를 좀 더 편하게 하기 위하여 단순화 시킨 도구라고합니다.

행(row)과 열(column)을 가지고 있으며 다음과 같이 표기합니다.

\begin{bmatrix} a & b\\ c & d \end{bmatrix}

또한 행이 하나이거나, 열이 하나인 경우를 볼 수 있는데, 모습이 마치 벡터와 같습니다.

그리고 이걸 수학적으로 행이 하나인 행렬은 행벡터(row vector) $\begin{bmatrix} a & b \end{bmatrix}$

열이 하나인 행렬은 열벡터(column vector) $\begin{bmatrix} a \\ b \end{bmatrix}$

라고 합니다.

행렬의 곱셈 연산정리

행렬의 곱셈은 선형변환에 사용할 수 있게 해주는 수학적 도구라고 하였는데,

정확히 어떻게 동작하는지 본다면 그 의미를 알 수 있을 것 같습니다.

일단 기본적으로 스칼라와 행렬의 곱은 단순하게도 모든 원소에 대해 스칼라배 해주는 것과 같습니다. 마치 벡터에서의 스칼라배와 마찬가지로 말이죠.

\bold A = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \\ k\bold A = \begin{bmatrix} ka & kb\\ kc & kd \end{bmatrix}

그리고 메인인 행렬과 행렬의 곱셈을 알아봅시다.

간단하게 행렬의 곱은, 행과 열끼리 곱연산한 결과의 합을 저장합니다.

행렬 $\bold A$ 와 $\bold B$ 의 곱은 $\bold{AB}$ 로 쓰고, 다음과 같이 정의합니다.

” $\bold{AB}(i,j)$ 는, $\bold A$ 의 $i$ 번째 행이 이루는 행벡터와 $\bold B$ 의 $j$ 번째 열이 이루는 열벡터의 내적이다”

무슨소리냐고요?

5%20Linearity,%20Matrix%20multiple,%20Polar%20Coordinate%2078227d285b464a5390577089f1b1e20d/assignment_GIF_5.gif

이것은 처리를 시각적으로 보여준 것입니다.

자 이제 더 자세하게 알아봅시다.

행렬 곱셈 연산이 가지는 성질 정리

행렬의 곱연산이 가지는 성질이라. 일단은 제일 만만한 행이 하나거나, 열이 하나인 행벡터와 열백터를 두고 생각해 봅시다.

\bold A \vec v =\begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy \end{bmatrix} = \bold u

\bold A \vec v =\begin{bmatrix} a & b\\ c & d\\ e & f \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy\\ ex+fy \end{bmatrix} = \bold u

어떤 행렬에 열벡터를 곱하였더니 새로운 열벡터가 나왔습니다.

이 과정은 m개의 행과 n개의 열을 가진 행렬 $\bold A$ 를 n차원 벡터에 작용시켜 m차원 벡터를 만드는 것 아닐까요?

그렇습니다. 행렬은 함수와 같습니다.

어떤 입력값을 통해 출력값을 대응하는데, 이 출력값 역시 동일한 체계를 가지고 있습니다.

즉 행렬의 곱셈은 사상(mapping)입니다. 사상이란 말은 저에게 조금 낯설다보니, $\bold u$ 의 경우 각 성분이 기존 성분 $x,y$ 의 선형결합이므로 선형변환(Linear Transformation) 이라 말해도 되겠군요

자 여기서 잠시, 그러면 m과 n이 동일하다면 동일한 차원의 벡터가 나오겠죠?

이걸 조금 더 분석해봅시다.

\bold A \vec v =\begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy \end{bmatrix} = \bold u

라면

$\begin{cases} x \mapsto ax+by \\ y \mapsto cx+dy \end{cases}$ 입니다. 아, $\mapsto$ 는 mapsto, 대응관계를 나타냅니다.

그렇다면 여기서 항상 같은 꼴이 나올려면 어떡해야할까요?

$\begin{cases} x \mapsto 1x+0y \\ y \mapsto 0x+1y \end{cases}$ 라면 $\begin{cases} x \mapsto x \\ y \mapsto y \end{cases}$ 가 될 수 있겠죠?

\therefore a = 1, b=0,c=0,d=1 \\ \space \\ \bold A \vec v =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 1x+0y\\ 0x+1y \end{bmatrix} = \begin{bmatrix} x\\ y \end{bmatrix} = \bold u \\ \space\\ \space \\ \bold A \vec v =\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1x + 0y + 0z\\ 0x + 1y + 0z\\ 0x + 0y + 1z \end{bmatrix} = \begin{bmatrix} x\\ y\\ z \end{bmatrix} = \bold u

이렇게 열의 수 = 행의 수 = $k$ 인 행렬에서 $a_{00},a_{11},a_{22} ... a_{kk}$ 의 값만 1인 행렬을

항등행렬(identity matrix) 혹은 단위행렬 이라고 합니다. 기호로는 $\bold I$ 를 사용합니다.

그렇다면 이 대각선에만 값을 가지는 행렬에 1이 아닌 숫자를 가지게 된다면, 벡터의 각 성분에만 배율을 줄 수 있지 않을까요?

아무튼 그렇습니다.

회전 변환을 행렬로 표현

아까 설명했던 선형변환을 다시 생각해봅시다.

\bold A \vec v =\begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} ax+by\\ cx+dy \end{bmatrix} = \bold u

그러면 이건 이렇게 변환된다고 볼 수 있습니다.

\begin{cases} x \mapsto ax+by \\ y \mapsto cx+dy \end{cases}

그리고 저번주차의 과제물, 회전변환에서 식을 인용하자면

(x,y)=x\cdot e_1+y\cdot e_2 \\ v'=x\cdot (cos\theta, sin\theta)+y\cdot (-sin\theta, cos\theta) \\ v'=(x\cdot cos\theta-y\cdot sin\theta, x\cdot sin\theta+y\cdot cos\theta)

과 같이 됩니다.

이걸 이제 임의의 변환용 행렬 $\bold A$ 에 대하여 $v'$ 을 결과로써 표현한다면

\bold A \vec v =\begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} x\cdot cos\theta-y\cdot sin\theta\\ x\cdot sin\theta+y\cdot cos\theta \end{bmatrix} = v' \\ \space \\ \therefore \bold A = \begin{bmatrix} cos\theta &-sin\theta \\ sin\theta &cos\theta \end{bmatrix}

짜잔. 회전변환을 행렬로써 만들어 둘 수 있게 됩니다.

이렇게 선형변환을 이루는 것이 행렬곱셈이라고 생각합니다.

이제 다시 성질을 정리해보죠.

교환법칙 : 비가환적(Not communicative)

AB = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \cdot \begin{bmatrix} e & f\\ g & h \end{bmatrix} = \begin{bmatrix} a\cdot e + b\cdot g & a\cdot f + b\cdot h \\ c\cdot e + d\cdot g & c\cdot f + d\cdot h \end{bmatrix}

BA = \begin{bmatrix} e & f\\ g & h \end{bmatrix} \cdot \begin{bmatrix} a & b\\ c & d \end{bmatrix} = \begin{bmatrix} a\cdot e + c\cdot f & b\cdot e + d\cdot f \\ a\cdot g + c\cdot h & b\cdot g + d\cdot h \end{bmatrix}

연산 순서의 변경은 치명적으로 작동합니다.

결합법칙 : 성립

일단 전제조건을 걸어야 할 것 같습니다.

$\bold A$ 의 열의 개수 = $\bold B$ 의 행의 개수 = $\alpha$

$\bold B$ 의 열의 개수 = $\bold A$ 의 행의 개수 = $\beta$

\bold{(AB)C} = ( \begin{bmatrix} a & b\\ c & d \end{bmatrix} \cdot \begin{bmatrix} e & f\\ g & h \end{bmatrix} ) \cdot \begin{bmatrix} i & j\\ k & l \end{bmatrix} = \begin{bmatrix} a e + b g & a f + b h \\ c e + d g & c f + d h \end{bmatrix} \cdot \begin{bmatrix} i & j\\ k & l \end{bmatrix} \\ = \begin{bmatrix} ((a e + b g) i + (a f + b h) k & ((a e + b g) j + (a f + b h) l) \\ ((c e + d g) i + (c f + d h) k) & ((c e + d g) j + (c f + d h) l) \end{bmatrix} \\ = \begin{bmatrix} a e i+ b g i + a f k+ b h k & a e j+ b g j + a f l+ b h l \\ c e i+ d g i + c f k+ d h k & c e j+ d g j + c f l+ d h l \end{bmatrix}

\bold{A(BC)} = \begin{bmatrix}a & b\\c & d\end{bmatrix} \cdot(\begin{bmatrix}e & f\\g & h\end{bmatrix} \cdot \begin{bmatrix}i & j\\k & l\end{bmatrix}) = \begin{bmatrix}a & b\\c & d\end{bmatrix} \cdot \begin{bmatrix}e i + f k & e j + f l \\g i + h k & g j + h l\end{bmatrix} \\ = \begin{bmatrix} a (e i + f k) + b (g i + h k) & a (e j + f l) + b (g j + h l) \\ c (e i + f k) + d (g i + h k) & c (e j + f l) + d (g j + h l) \end{bmatrix} \\ = \begin{bmatrix} a e i + a f k + b g i + b h k & a e j + a f l + b g j + b h l \\ c e i + c f k + d g i + d h k & c e j + c f l + d g j + d h l \end{bmatrix}

두 식은 내려가게 된다면 곱셈의 결합법칙 및 덧셈의 교환법칙에 의해 같다는걸 알 수 있습니다.

$\therefore$ 행렬의 곱셈에서는 결합법칙이 성립합니다.

분배법칙 : 성립

수식쓰다가 오타나면 죽을 것 같습니다.

어짜피 행렬은 모든 원소에 행해지는 연산이 동일하다고 볼 수 있습니다.

대충 3개의 행렬의 곱을 코드로 표현하면 이런 꼴 아닐까요?

  
//Mat = A*B*C
for(var h = 0; h < beta ;++h)
{
	for(var k = 0; k < alpha; ++k)
	{
		Mat[i,j] += (A[i,k] * B[k,h] * C[h,j])
	}
}

그러면 하나의 연산을 기준으로 이번에는 한번 프로그래머스럽게(?) 해보자구요.

일단 행렬의 덧셈연산은 같은행,같은 열끼리 더한것과 같다고 하였습니다. 즉 $\bold{B}+\bold{C} = [(b_{ij}+c_{ij})]$ 라고 가정합니다.

그리고 아까의 가정도 여전히 놔둡시다.

$\bold A$ 의 열의 개수 = $\bold B$ 의 행의 개수 = $\alpha$

또한 $\bold {AB} = \bold X$ 라 가정할때, $\bold X$ 의 원소 $x_{ij}$ 는 다음과 같이 수학적으로? 정의할 수 있습니다

x_{ij} = \sum_{k=1}^{\alpha} a_{ik}b_{kj} = (a_{i1}b_{1j} + .. a_{i\alpha}b_{\alpha j})

그러므로 이에 따라 분배법칙을 다시 정리해보죠

\bold{A}(\bold{B}+\bold{C})(i,j) = \sum _{k=1}^{\alpha}a_{ik}(b_{kj}+c_{kj}) = \sum_{k=1}^{\alpha}(a_{ik}b_{kj} + a_{ik}c_{kj}) \\ = \sum _{k=1}^{\alpha}a_{ik}b_{kj} + \sum _{k=1}^{\alpha}a_{ik}c_{kj} \\ = \bold{AB}(i,j) + \bold{AC}(i,j)

$\therefore$ 행렬의 곱셈에서는 분배법칙도 성립합니다.

전치연산

전치(Transpose)는 행과 열을 뒤바꾼 것입니다.

Transpose의 T를 따와 $\bold{A}$ 의 전치행렬을 $\bold{A}^{T}$ 라고 표현합니다.

행과 열을 뒤바꾼 것이기에 $(\bold{A}^{T})^T = \bold A$ 입니다.

\bold A = \begin{bmatrix} a & b & c\\ d & e & f \end{bmatrix} , \bold A^T = \begin{bmatrix} a & d\\ b & e\\ c & f \end{bmatrix}

과 같이 표현할 수 있습니다.

행벡터 및 열벡터에 대해서도 전치연산을 할 수 있는데, 이때 나오는 결과는 행렬이 바뀌였기때문에 행벡터 $\mapsto$ 열벡터 , 열벡터 $\mapsto$ 행벡터 입니다.

아까 설명했던 대각선 값과 하여 재미있는게 생각났습니다.

원본과 전치연산을 행한 사본을 곱하면 어떻게될까요?

\bold A = \begin{bmatrix} a & b & c\\ d & e & f \end{bmatrix} , \bold A^T = \begin{bmatrix} a & d\\ b & e\\ c & f \end{bmatrix} \\ \bold {AA}^T = \begin{bmatrix} a a + bb + cc & ad + be + cf\\ ad + be + cf & dd + ee + ff \end{bmatrix}

무려 대각선을 기준으로 대칭인 행렬이 됩니다.

이런 행렬은 대칭행렬(symmetric matrix)라고 부른다더군요.

이걸 언제쓰는지는 저도 모르겠습니다.

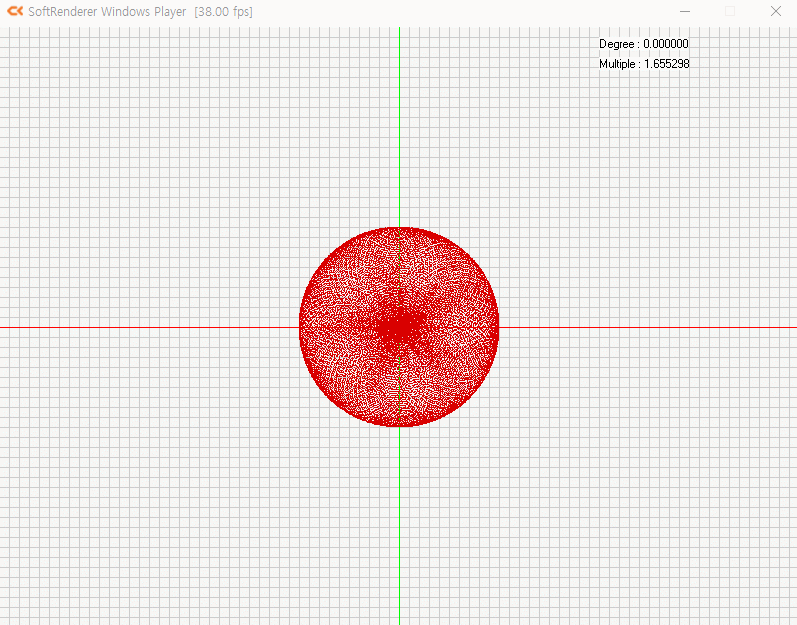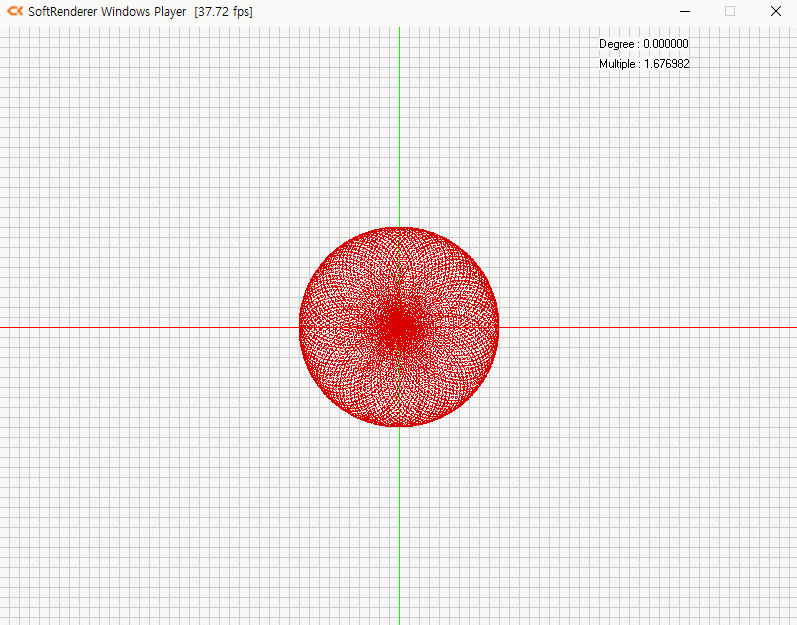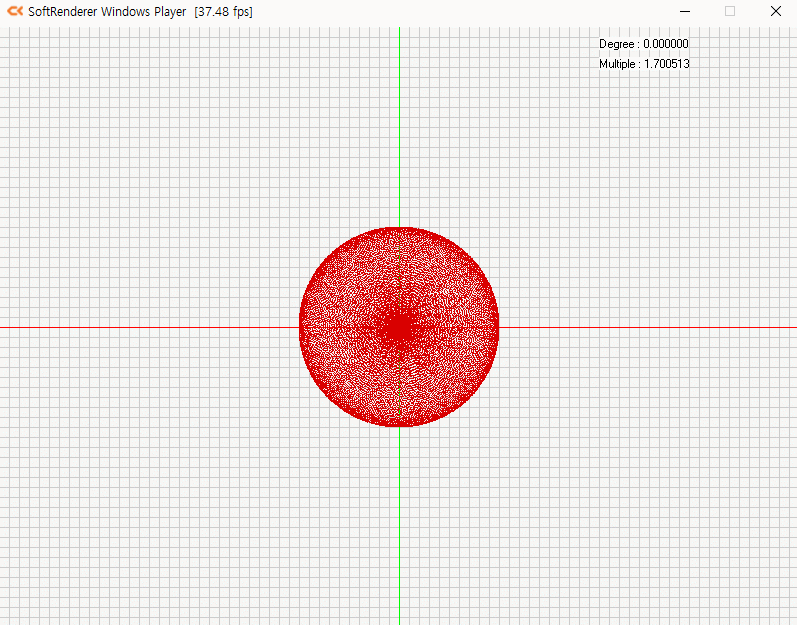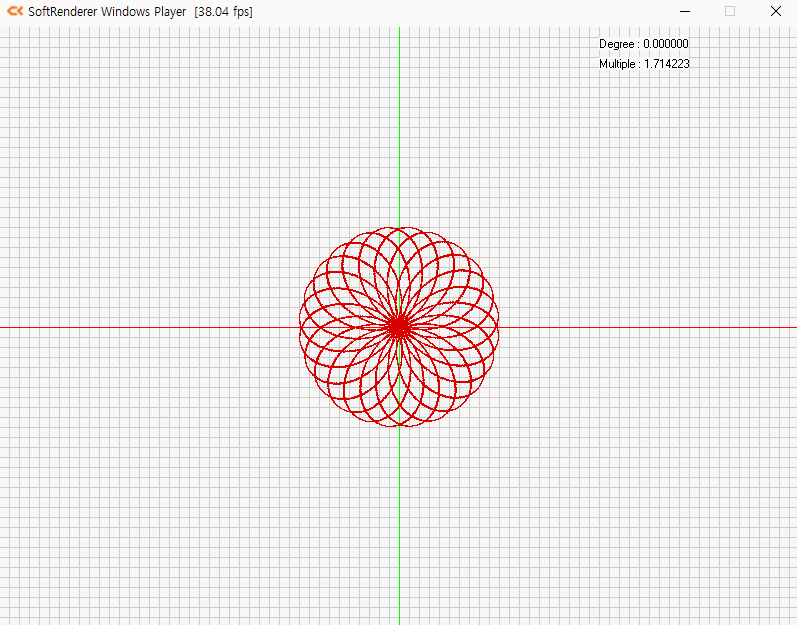
극좌표계 활용 및 표현

Untitled%201.png

5%20Linearity,%20Matrix%20multiple,%20Polar%20Coordinate%2078227d285b464a5390577089f1b1e20d/assignment_GIF_6.gif

r = sin(a \cdot \theta)

극 좌표계에서 $sin(\theta)$ 를 통해 원을 그릴 수 있습니다.

그리고 그 주기를 조절한다면 겹쳐진 원을 만들 수 있죠. 그래서 한번 만들어 보았습니다.

앗! 정리되지 않은 미사용 소스가 일부 들어있을 수 있습니다

https://gist.github.com/ashuatz/fde778e98f9dba9fac0e91fe54c1e03d

y=ax+b는 왜 선형성을 만족하지 않을까?

선형변환을 시각적으로 본다면, 변하지 않는 사실이 두가지가 있습니다.

기저벡터를 기준으로 그리드를 그렸을 때, 그리드는 평행하다는 사실과,

원점은 움직이지 않는다 입니다.

즉 무언가를 할 때 마다 원점이 바뀌게 된다면, 이는 선형적이지 않다고 볼 수 있는게 아닐까요?

혹은 입력의 반대를 넣어서 과거로 돌아갈 수 없다면, 이는 선형적이지 않다고 생각하는게 아닐까요?

같은 크기의 반대부호를 가지는 스칼라배를 통해 원점으로 돌아갈 수 없다면, 예측도, 보간도, 보외도 아무것도 할 수 없게되니 선형적이지 않죠. 일종의 하나의 상태로만 흐를 수 있는 일방통행이 되기 때문이라고 생각합니다.

5. Linearity, Matrix - multiple