4.Triple Product & Perspective Projection

Triple Product & Perspective Projection

머리말

---

작성일 기준 벌써 추석입니다.

다들 연휴를 잘 즐기셨는지는 모르겠지만 저는 추석에도 과제를 하고 있습니다.

삼중곱(Triple Product)

---

삼중곱이란 무엇일까요. 삼중곱 혹은 삼중 벡터곱은 벡터 3개를 곱하는 방법을 말하는 것입니다.

그러면 총 4개의 케이스중 성립하는 것을 정리해 봅시다.

• $u\cdot(v\cdot w)$ 내적의 결과는 스칼라이기 때문에 스칼라와 벡터의 내적은 성립이 불가합니다.
• $u\cdot(v\times w)$ 스칼라 삼중곱
• $u\times(v\cdot w)$ 내적의 결과는 스칼라이기 때문에 스칼라와 벡터의 외적은 성립이 불가합니다.
• $u\times(v\times w)$ 벡터 삼중곱

이 중 정의가 불가능한 삼중곱들을 제외한 두 삼중곱을 소개하려합니다.

스칼라 삼중곱(Scalar Triple Product)

---

스칼라 삼중곱은 두 벡터의 외적(벡터곱,cross product)를 나머지 벡터와 내적(스칼라곱,dot product)한 것으로 정의합니다.

$u\cdot(v\times w)$ 로 표기하며, 괄호가 없어도 논리적으로 내적을 먼저 진행하면 외적이 불가하기 때문에 괄호없이 표기하기도 합니다.

기하학적 의미

---

삼중곱에 사용되는 세개의 벡터로 정의되는 평행육면체의 부피와 같습니다.

이유또한 단순합니다.

중학교 수학(8)에서 저희는 평행선과 삼각형의 넓이에서

밑변이 같다면 아래와 같은 다른 한 점이 평행선의 어디에 있던

같은 넓이를 가진다는것을 배웠습니다.

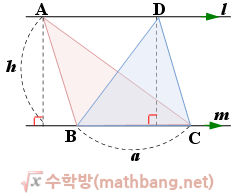
평행선과 삼각형의 넓이 - mathbang.net

이 개념을 이제 3차원으로 끌고와서 처리하면 됩니다.

$(v\times w)$ 는 결론적으로 $(v, w)$ 로 구성된 평면과 직교하는 벡터입니다.

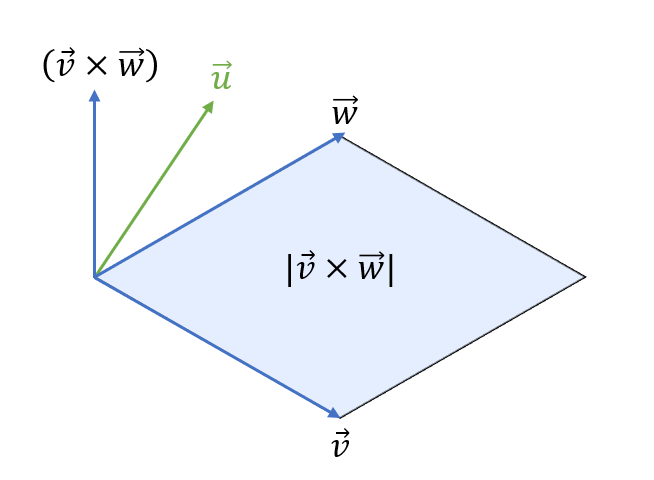
$(v\times w)$ 와 $u$ 를 내적한다면

와 같은 형태가 되는 것입니다.

그래서 기하학적 의미가 평행육면체의 부피라고 한 것입니다.

추가적으로 결국 세개의 벡터는 변하지 않기 때문에, 순서만 잘 맞춰준다면 다음 꼴이 만족합니다.

$$\vec{u}\cdot\left(\vec{v}\times\vec{w}\right)=\vec{v}\cdot\left(\vec{w}\times\vec{u}\right)=\vec{w}\cdot\left(\vec{u}\times\vec{v}\right)$$

또한 이 값은 세 벡터를 행벡터 혹은 열벡터로 갖는 3x3 행렬의 행렬식입니다.

뭐 당연하긴 하죠. 행렬식의 값의 뜻이 2차원에서는 두 벡터로 만들어지는 평행사변형의 넓이였으니까요.

3차원의 행렬식

---

det(A)= 0일 때,

3차원 공간에 속한 임의의 벡터로 접근이 불가합니다.

이걸 외적과 내적으로 본다면?

$(v_1 \times v_2) \cdot v_3 = 0$ 이며, $v_1$ 와 , $v_2$ 로 만든 평면에 , $v_3$ 가 속한다고 볼 수 있습니다.

다시 말하면, 세 벡터의 선형조합으로 ‘3차원 공간에서의’ 새로운 벡터의 생성이 불가하다.

$\therefore$ 스칼라 삼중곱은 determinant와 같다.

벡터 삼중곱(Vector Triple Product)

---

벡터 삼중곱은 두 벡터의 외적에 다시 다른벡터와 외적한것을 말합니다.

수식으로는 다음과 같이 씁니다.

$$\vec{u}\times(\vec{v}\times\vec{w})$$

벡터 삼중곱 전개(Triple Product Expansion)

---

라그랑주 공식, 라그랑주 익스팬션이라고 보통 많이 합니다.

그 노가다 한번 해볼까요?

$$\vec{v}\times\vec{w}=(v_yw_z-w_yv_z,\ v_zw_x-w_zv_x,\ v_xw_y-w_xv_y)\\ =(t_x,t_y,t_z)\\ (\vec{u}\times\vec{t})_x = u_yt_z-t_yu_z\\ \\\quad\\ = u_y(v_xw_y-w_xv_y)-u_z(v_zw_x-w_zv_x)\\ =(u_yv_xw_y-u_yw_xv_y)-(u_zv_zw_x-u_zw_zv_x)\\ =(u_yv_xw_y-u_yv_yw_x-u_zv_zw_x+u_zv_xw_z)\\ =v_x(u_yw_y+u_zw_z) -w_x(u_yv_y+u_zv_z)$$

예전에 인수분해 할 때를 기억해서,

여기에 비어있는, 존재하지 않는 성분인 $+u_xv_xw_x-u_xv_xw_x(=0)$ 를 넣어주면

재미있게 정리가 됩니다.

$$=(u_xv_xw_x+u_yv_xw_y+u_zv_xw_z)-(u_xv_xw_x+u_yv_yw_x+u_zv_zw_x)\\ =v_x(u_xw_x+u_yw_y+u_zw_z)-w_x(u_xv_x+u_yv_y+u_zv_z)$$

이는 내적으로 정리하면 다음과 같습니다.

$$=v_x(\vec{u}\cdot\vec{w})-w_x(\vec{u}\cdot\vec{v})$$

나머지 성분에 대해서도 동일하게 진행되므로 다음의 식이 성립합니다.

$$\vec{u}\times(\vec{v}\times\vec{w})=(\vec{u}\cdot\vec{w})\cdot\vec{v}-(\vec{u}\cdot\vec{v})\cdot\vec{w}$$

또한 순서를 바꿔 반수성질을 이용하여 다음과 같이 전개할 수 있습니다.

$$(\vec{u}\times\vec{v})\times\vec{w}\\=-\vec{w}\times(\vec{u}\times\vec{v})\\ =-(\vec{v}\cdot\vec{w})\vec{u}+(\vec{u}\cdot\vec{w})\vec{v}$$

짠

원근 투영 변환(Perspective Projection Transformation)

---

하….

직교하는 세 축을 다음과 같이 화각(Field of view, FOV)을 매개로 하는 사각뿔 공간으로 변경해야합니다.

그것이…『Perspective View』니까…

화각을 매개로하는 화면 구성

그러면 앞과 뒤, 거리 같은 정보를 하나로 모은

투영 평면(마치 아핀공간이 생각나지 않나요?)이 필요합니다.

그러나 이 공간의 특수성은… z 값에 따라 xy평면이 영향을 받는다는게 중요합니다.

즉 의존성이 발생하는 것이죠.

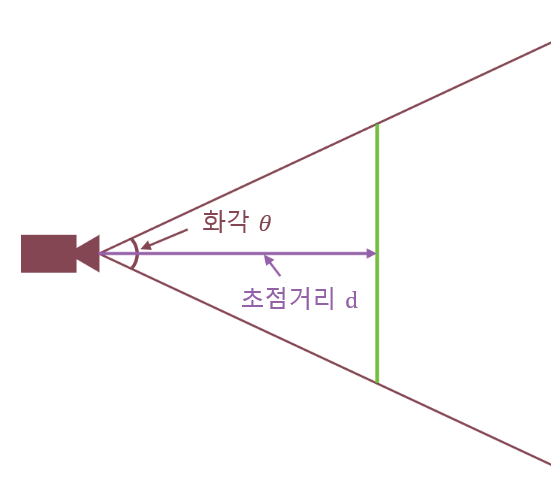
일단 정규화 해서 처리합시다.

정규화요?Normalize요.

NDC(Normalized Device Coordinate)

---

Nexon Developers Conference

(재활용)

일단 첫번째,

초점거리 d에 대해, 삼각 함수를 사용하면 다음과 같은 식이 성립합니다. (단, $0<\theta<180$ )

$$d=\frac{1}{tan(\frac{\theta}{2})}$$

두번째, 비례식을 사용해서 다음과 같은 식들을 구할 수 있습니다.

$$n_y:d=v_y:-v_z\\$$

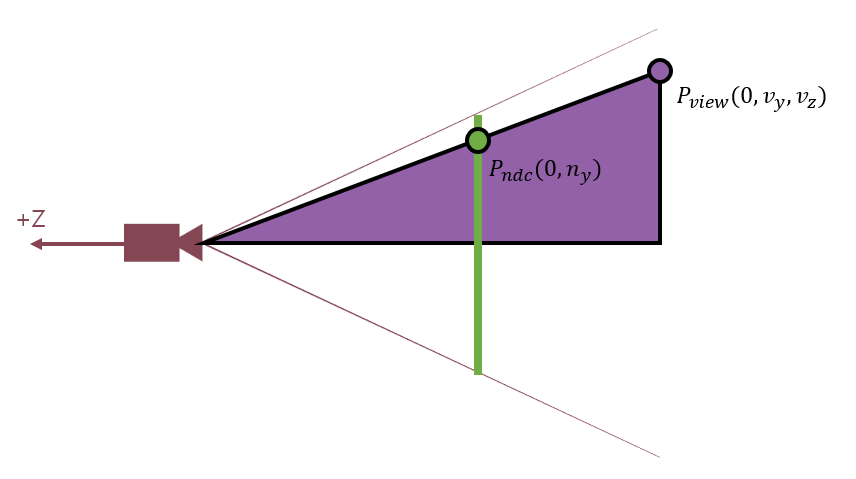
사영 공간에서 X축과 Y축은 같은 시야각을 가지고 직교하므로 X축도 동일하게 구현이 가능합니다.

$$n_y=\frac{d\cdot v_y}{ {-v}_z} \\ n_x=\frac{d\cdot v_x}{ {-v}_z}$$

일반화하면 다음과 같죠.

$$P_{ndc}=\left(\frac{d\cdot v_x}{ {-v}_z},\frac{d\cdot v_y}{ {-v}_z}\right)=-\frac{d}{v_z}(v_x,v_y)$$

결론적으로 보자면 z값에 따라 x와 y값을 이동한다와 같습니다.

자 이제 모니터의 종횡비를 고려해 봅시다.

보통 종횡비(aspect Ratio)는 x:y로 표기하며, 따라서 다음과 같습니다.

$$a=\frac{width}{height}$$

그리고 이걸 미리 구워둬서 x축에 계산한다면, 최종적으로 화면에 1대1 맵핑하더라도 찌그러지지 않겠죠.

$$P_{ndc}=-\frac{d}{v_z}(\frac{v_x}{a},v_y)$$

최종적으로 행렬로써 표현하자면 다음과 같습니다.

$$P\cdot v=[\begin{matrix}\frac{1}{a}\cdot\frac{d}{-v_z}&0\\0&\frac{d}{-v_z}\\\end{matrix}]\cdot[\begin{matrix}v_x\\v_y\\\end{matrix}]$$

하지만 이 행렬은 문제가 하나 있죠.

위 행렬이 가지는 문제점 (행렬로 왜 NDC를 만들 수 없는가)

---

$-v_z$ 의 값은 정점 좌표마다 다른데, $-v_z$ 로 나눠야 한다는 점에서 매 점마다 새로운 행렬을 만들어야합니다.

말이 안되는 소리죠 그럴꺼면 행렬을 왜씁니까.

그러면 일단 간단하게 $-v_z$ 를 제거하는 방향으로 진행해 봅시다.

클립 공간(Clip Space)

---

a와 d는 거의 상수와 같습니다.

그러니 $v_z$ 가 행렬에 낄 수 없도록 행렬을 개조합니다.

일단 축을 확장합니다.

$$P_{ndc}=(\frac{d\cdot v_x}{-v_z\cdot a},\frac{d\cdot v_y}{-v_z},1)\\$$

동차 좌표계에서 직교 좌표계로 변환할때는 각 성분에 마지막 차원의 값을 나누고 마지막 차원을 빼는 방법이 있습니다.

그렇게 ‘나눈다’는 개념이 NDC 에서 못한 $v_z$ 나누기를 진행해줄 수 있습니다.

$$\rightarrow P_{clip}=(\frac{d\cdot v_x}{a},d\cdot\ v_y,-v_z)$$

결론적으로 다음과 같은 행렬의 구성이 되는 것이죠.

$$P\cdot\ v=\left[\begin{matrix}\frac{d}{a}&0&0\\0&d&0\\0&0&-1\\\end{matrix}\right]\left[\begin{matrix}v_x\\v_y\\v_z\\\end{matrix}\right]=\left[\begin{matrix}\frac{d}{a}\cdot v_x\\d\cdot v_y\\-v_z\\\end{matrix}\right]$$

그러면 아까 그냥 슬쩍 넘긴 동차 좌표계의 개념에 대해 정리를 다시 해볼까요?

동차 좌표계(Homogenous Coordinate System)

---

One of the many purposes of using homogeneous coordinates is to capture the concept of infinity. In the Euclidean coordinate system, infinity is something that does not exist. Mathematicians have discovered that many geometric concepts and computations can be greatly simplified if the concept of infinity is used. This will become very clear when we move to curves and surfaces design. Without the use of homogeneous coordinates system, it would be difficult to design certain classes of very useful curves and surfaces in computer graphics and computer-aided design.

동차 좌표를 사용하는 많은 목적 중 하나는 무한대의 개념을 포착한다는 것입니다. 유클리드 좌표계에서는 무한대는 존재하지 않습니다. 수학자들은 무한대 개념을 사용하면 많은 기하학적 개념과 계산이 단순화 될 수 있음을 발견하였습니다. (중략)

Homogeneous Coordinates - michigan technological university

점이 카메라로부터 멀어질 수록 투영된 위치는 원점을 향하게 된다.

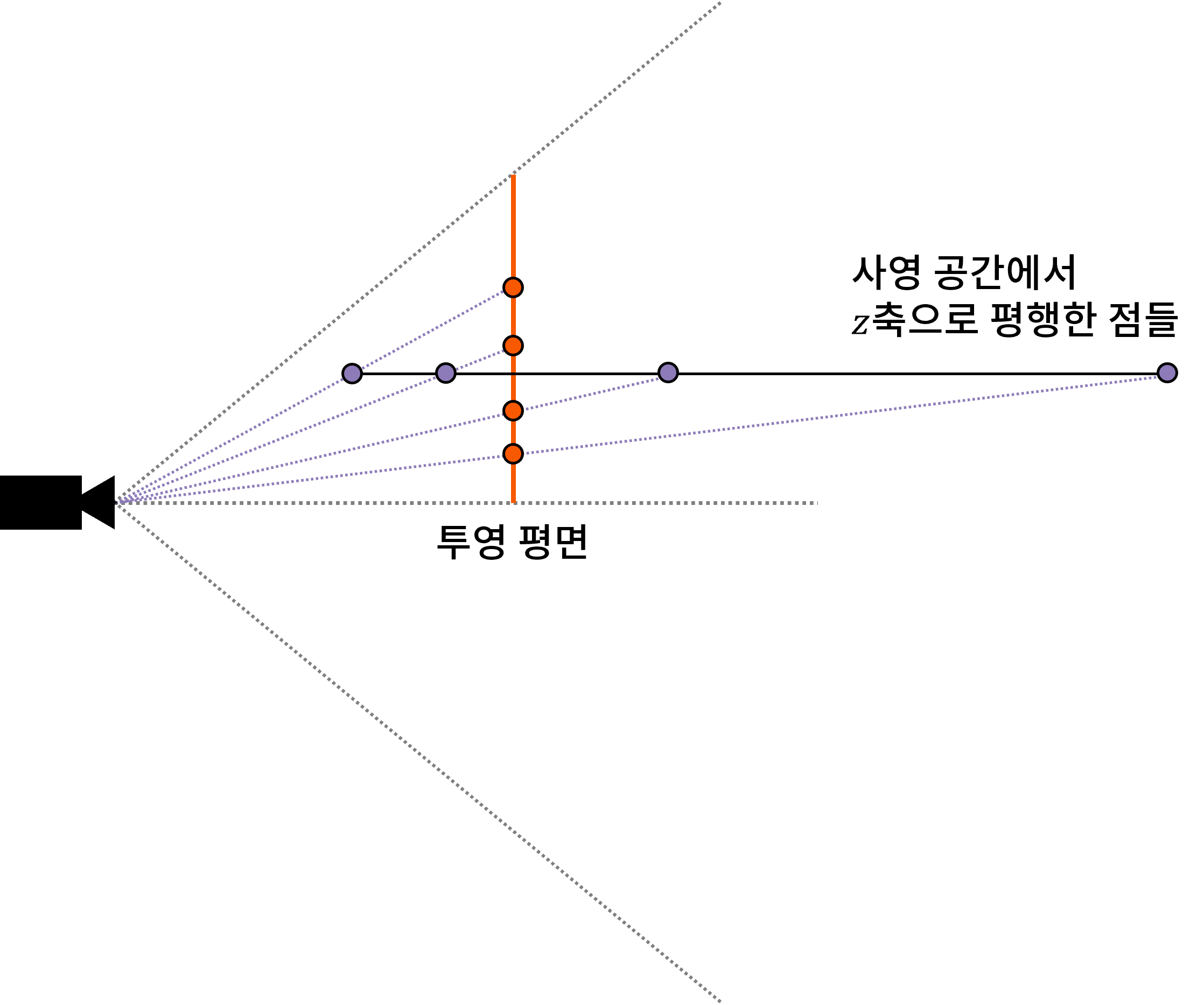
아핀공간을 한번 생각해봅시다. 사실 투영한 2차원 화면좌표 역시 3차원 공간이였다면 어떨까요?

지금 보는 2차원 평면의 좌표 $(x,y)$ 는 기존 3차원의 좌표 $(x', y', z')$ 을 투영한 결과입니다.

그걸 다시 변환되었다고(mapsto) 생각해봅시다.

$$(x',y',z')\mapsto(x,y,1)$$

그렇다면 $(x, y)$ 를 $(x', y', z')$ 으로 표현해 봅시다.

$$x = \frac{x'}{z'} \\ y = \frac{y'}{z'}$$

직선의 방정식( $y=ax+b$ )의 꼴로 표현하면 다음과 같습니다.

$$\frac{y^\prime}{z^\prime}=a\frac{x^\prime}{z^\prime}+b$$

양변에 $z'$ 를 곱하면 다음과 같이 전개되는데,

$$y^\prime=ax^\prime+bz^\prime$$

위 식은 상수항이 없이 모든 항이 동일한 차수를 가집니다.

그래서 동차(같은 차) 방정식(Homogenous Equation)이라고 부릅니다.

소실점의 원리

---

소실점

간단하게 멀리 있는 값이 커질때 이므로,

극한( $\lim\limits_{v_z\rightarrow\infin})$ 으로 생각하면, 오히려 쉽습니다.

$$P_{ndc}=(\frac{d\cdot v_x}{-v_z\cdot a},\frac{d\cdot v_y}{-v_z},1)\\$$

에서 $-v_z$ 가 $\infin$ 로 간다면 (0,0,1)이라는 값을 갖게 되겠죠.

그래서 재미있는게 있습니다.

포물선은 사실 원과 유사한데, 소실점이 있으면 확실하게 볼 수 있다는 것이죠.

Circular Parabola

https://www.youtube.com/watch?v=ukmqwGbfEZM

맺으며

---

이것을 끝으로 제 턴을 끝내도록 하겠습니다.