4. 삼각함수

삼각함수

삼각형에 관련된 단어를 아는만큼 정리하고 영단어 함께 표기

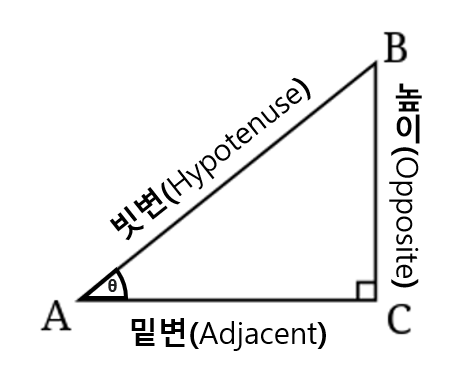
직각삼각형(Right-Angled Triangle)

• 변(Edge)
  • 빗변(Hypotenuse)
  • 높이(Opposite) : 각과 마주보기 때문에 Opposite(마주보는 변)
  • 밑변(Adjacent) : 각에서 인접하였기 때문에 Adjancent(인접한 변)

…저는 삼각형에 대해 아는 것이 없었습니다.

---

삼각비와 삼각함수의 차이를 정리

삼각비 (Trigonometric Ratio) : 어떠한 각도에 대한 두개의 변에 대한 정의입니다.

sin,cos,tan,csc,sec,cot의 3+3개(3가지의 비율 및 역원(inverse))로 정의됩니다.

각 A에 대해 빗변, 높이, 밑변을 H O A라고 가정할 때,

삼각비

역원(Multiplicative Inverse)

두 변

sin A = O / H

csc A = H / O

(빗변과 높이)

cos A = A / H

sec A = H / A

(빗변과 밑변)

tan A = O / A

cot A = A / O

(밑변과 높이)

로 정의합니다.

삼각함수(Trigonometric function) : 함수입니다. 각과 변의 길이를 대응시킨 수학적 함수와 같으며,

정의역(Domain)과 치역(Range)이 정의되어 있습니다.

예를 들어 $y= sin(x)$에 대해 $\mathbb R$이라는 정의역(Domain)과 $[-1,1]$의 치역(Range)를 갖는 ‘함수’입니다.

---

삼각함수에 관련된 공식을 아는만큼 정리

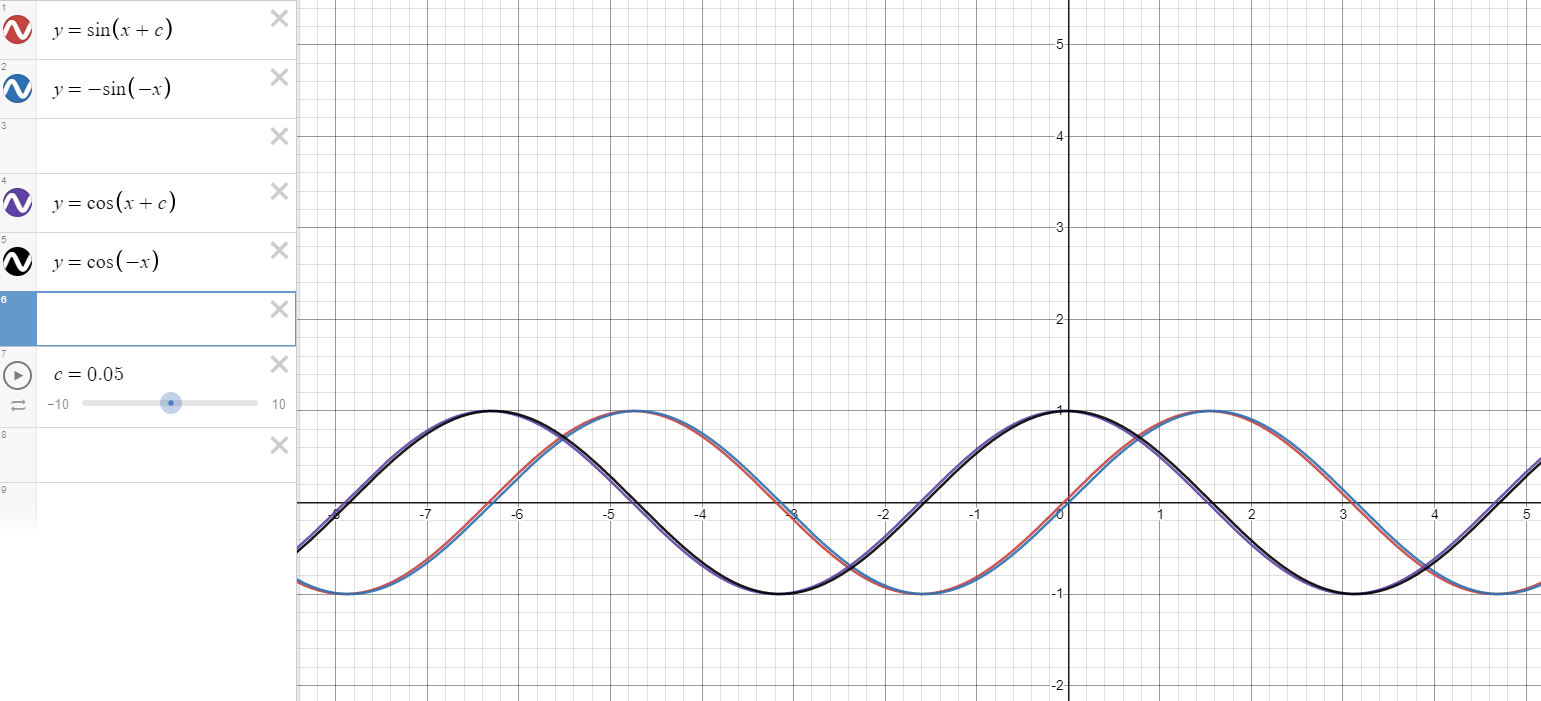
코사인과 사인함수의 성질

• 주기성
  • 진폭이 -1,+1 사이에서 진동하는 모양을 갖습니다.
  • 주기는 2$\pi$ 기준으로 반복됩니다.
• 대칭성
  • $$sin(\theta) = -sin(-\theta)$$
    • 점 대칭(기대칭, odd symmetry)
    • 원점을 기준으로 대칭
  • $$cos(\theta) = cos(-\theta)$$
    • y축 대칭(우대칭, even symmetry)
    • 수직축(Y)을 기준으로 대칭

대칭성 예시(같은 값을 가지면 그래프의 색상이 균일하게 나타나, 약간의 오프셋을 두었습니다)

---

공간변환의 관점에서 물체의 회전 메커니즘에 대해 정리

빗변을 벡터로 생각해봅시다.

빗변의 크기가 1인 원이 있다고 생각할 때

다음과 같은 원이 있습니다.

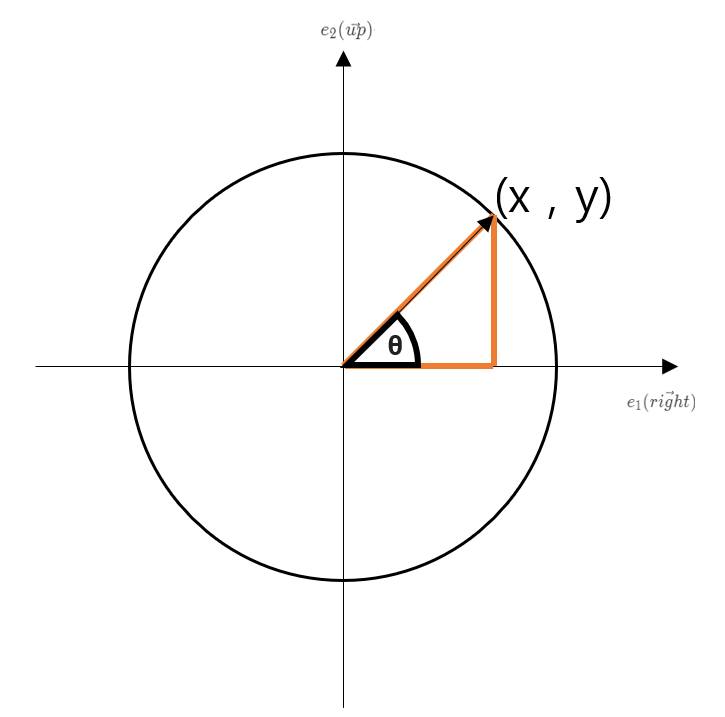
좌표값의 $(x,y)$는 엄밀히 따지고 보자면, 두 기저벡터와 x스칼라배, y스칼라배를 통한 선형조합으로 표현한다면 $(x \cdot e_1+y \cdot e_2)$입니다

$e_1(\vec{right})$과 $e_2(\vec{up})$에 대해 반시계방향으로 회전하는($\theta$ ⇒ 0 to 90)생각을 해 본다면

$e_1(\vec{right})$은

• x성분에 대해 1에서 시작해서 0으로 이동하고, 이후 -1로 이동한다
• y성분에 대해 0에서 시작해서 1로 이동하고, 이후 0으로 이동한다

$e_2(\vec{up})$는

• x성분에 대해 0에서 시작해서 -1로 이동하고, 이후 0으로 이동한다
• y성분에 대해 1에서 시작해서 0으로 이동하고, 이후 -1로 이동한다

저는 연역적으로 수학을 풀어낼 수 없으니,

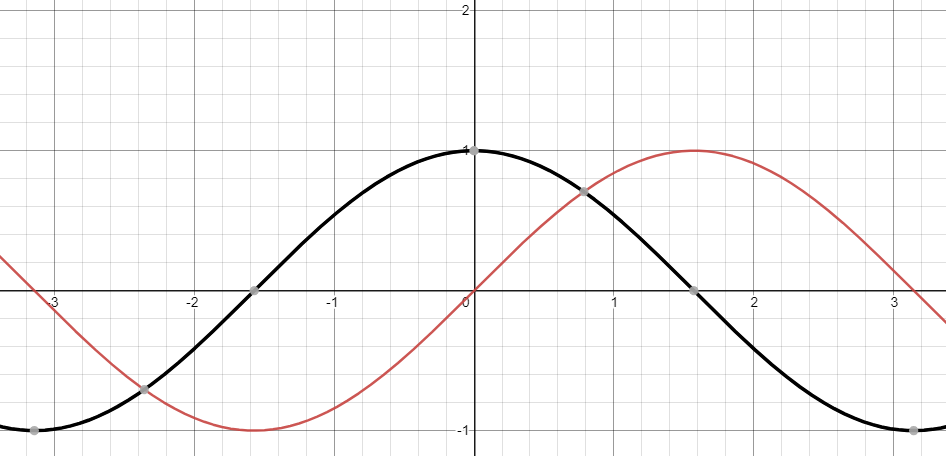
귀납적으로 매핑해 봅시다. (다홍색 : sin, 검정 : cos)

$$e_1(\vec{right})$$

• 1 →0은 cos 정방향, 이후 0→-1 역시 동일
• 0→1은 sin 정방향, 이후 1→0 역시 동일

$$e_2(\vec{up})$$

• 0→-1은 sin 역방향, 이후 -1→0 역시 동일
• 1→0은 cos 정방향, 이후 0→-1 역시 동일

만약 어느정도 x축으로 이동을 해도 같은 흐름을 가진 지형을 찾을 수 있겠지만

x축 이동 없이도 모두 처리가 되었습니다.

다만 여기서 역방향이 나오게 되는데, 이는 $\theta$대신 $-1 \cdot \theta$를 사용해야 합니다다.

하지만 $sin(-\theta) = -sin(- (-\theta))$에 의해 $-sin(\theta)$ 로 표현될 수 있습니다. (점대칭)

정리한다면

$$e_1(\vec{right}) = (cos(\theta),sin(\theta))$$ $$e_2(\vec{up}) = (-sin(\theta),cos(\theta))$$

짜잔. 두가지 축을 하나의 값에 의해 변경될 수 있는 상태로 바꾸었다.

이제 이 $\theta$의 값에 따라 공간은 회전하게 된다.

다시 맨 처음으로 돌아와서, 좌표는 $x \cdot e_1+y \cdot e_2$라고 하였다.

이 때, $e_1(\vec{right}) = (cos(\theta),sin(\theta))$, $e_2(\vec{up}) = (-sin(\theta),cos(\theta))$ 이므로

두 개를 성분별로 전개하면 $(x\cdot cos(\theta) - y\cdot sin(\theta) , x\cdot sin(\theta)+y\cdot cos(\theta))$ 가 된다.

다시 정리해 보자면,

$$(x,y)=x\cdot e_1+y\cdot e_2 \\ v'=x\cdot (cos\theta, sin\theta)+y\cdot (-sin\theta, cos\theta) \\ v'=(x\cdot cos\theta-y\cdot sin\theta, x\cdot sin\theta+y\cdot cos\theta)$$

이렇게 돌아간 정보를 돌아가지 않은($\theta = 0)$ 환경에서 보게 된다면 돌아간 좌표가 나오게 된다.

와! 이게 하니까 되네요

(영어가 너무 많이 들어간 줄간 간격이 짧은 글을 보니 머리가 어지러워서 조금 띄웠습니다)

(역시 줄 단위로 띄울게 아니라 정보량 단위로 정리하는게 좋을 것 같습니다.)

---

실습과제

입력 4축을 사용해 자유롭게 변환되는 물체를 표현하고 움짤 첨부

처음에는 시침과 분침을 생각해 두가지의 기저벡터를 회전시키는 단순한 로직을 짜봤습니다.

그리고 그 결과물을 보고있으니, y축 기저 벡터가 회전하지 않고 x축 기저벡터를 회전시킬때,

3차원적으로 회전한다는 느낌을 받았습니다.

그러면 여기서 끝낼 수 없죠. 자신이 있는 평면 몇 개를 준비하고, 그것이 존재하는 평면을 만듭니다.

시각적으로 꼬아봅시다.

• 원은 자신의 2차원 좌표계에서 회전합니다.
• 원이 속한 2차원 좌표계는 두개의 기저벡터중 하나,혹은 두개가 회전합니다.
• 다른방향으로 회전하는 독립적 2차원 좌표계를 갖는 원을 추가합니다.
• 이 2차원좌표계를 인풋에 의해 모두 회전시킬 수 있습니다.
• 그리고 이동은 원이 속한 2차원좌표계에서 이동하게 됩니다.

방향키 : 원이 속한 공간에서의 평행이동(x,y)

PageUp/PageDown/Home/End: 세개의 원이 속한 평면공간의 이동

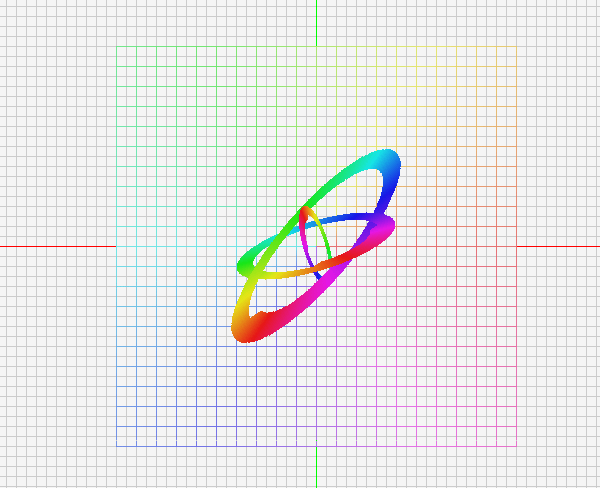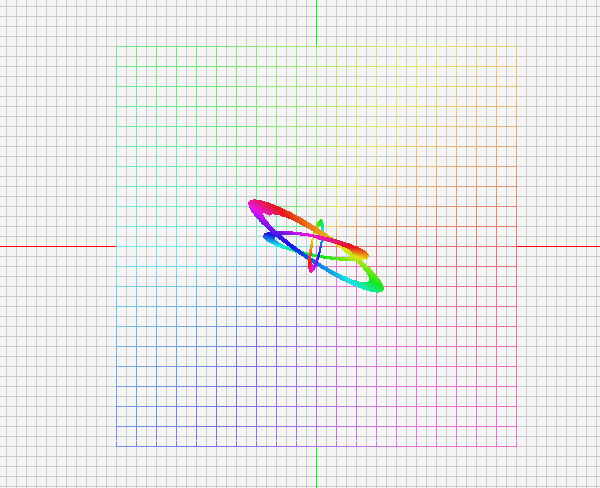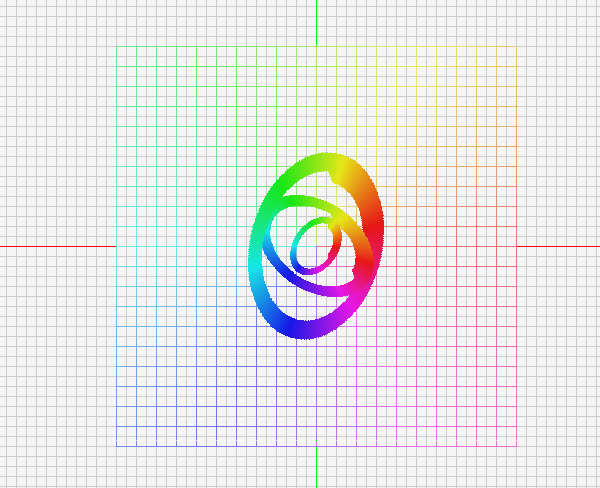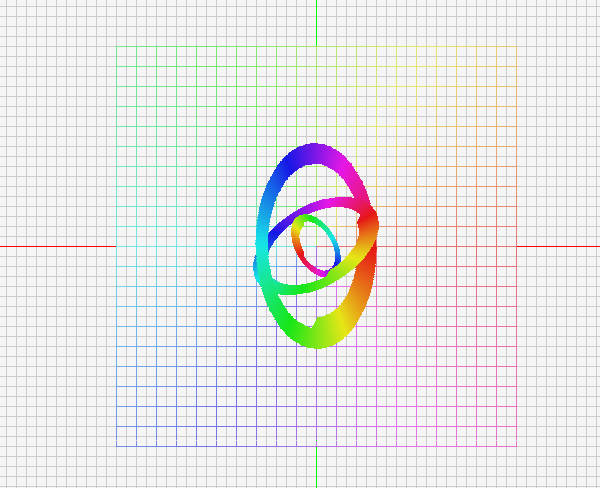
https://gist.github.com/ashuatz/ebbf2a422edbd9bc48795e2eddbbd735

---

추가

잠시 그림을 감상하다 생각난 것이 있습니다.

N차원 벡터가 N개의 기저벡터를 가진 공간이며, 3-tuple로 표현한다면

색상역시 3개의 기저벡터를 가진 3-tuple로 표현가능하다는것을 알았습니다

이 축을 R,G,B 축이라 가정할 때, 서로 각각의 색상은 다른색상에 영향을 미치지 않는 선형독립입니다.

그렇다면 2차원 좌표계에서 두가지 기저벡터로 색상을 분리할 수 있을까요?

HSV 색상영역에서 H와 S는 각각 선형독립이라고 할 수 있을까요?

HSV에서 H와 S 그리고 V는 서로 각각 독립입니다.

다만 RGB에서 본다면 H와 S는 서로 선형 의존관계라고 생각합니다.

S를 아무리 조절해도 G와 B가 바뀔 수 없으니까요.

하지만 H는 RGB를 모두 변경할 수 있습니다.

H는 RGB에서의 방향을 각도로 나타낸 것이고, s는 그 방향의 크기라고 생각합니다.

약간 극좌표계가 생각나는데, 극좌표계에 대해 아는 것도 없고 생각할 수 없다고 느껴 여기서 마무리 하겠습니다.

색상의 기저벡터를 변경(회전)하며 새로운 색상영역을 만들어 보는것도 시각적으로 재미있겠다고 생각하였는데, 2차원 평면에서 3차원(3개의 기저벡터를 갖는)영역을 다루려 하니 조금 어렵네요.

그래서 두개의 기저벡터를 갖기위해 HSV색상좌표계를 생각했는데(V를 고정으로 둔) H와 S에 대해 약간 생각하던 색상 벡터의 느낌과 다르게 구성되어있어 안타깝게도 생각을 포기했습니다.

H와 S가 축 이동에 의해 선형의존이 된다면, RGB가 선형의존이 된다면 어떤색상이 나올까요?

아마 세 벡터가 모두 선형의존이라면 빛 혼합에 의해 흰색이 나올것이라 생각합니다.

---