Backface Culling & Rodrigues rotation
서론

외적의 활용
외적의 활용에서 이어짐
백페이스 컬링(Backface Culling)
컬링이란?
보통 컬링(culling)은 특성에 따라 그룹에서 분리하는 과정을 뜻합니다.
저희쪽에서는 렌더링을 할지를 결정한다고 보면 될 것 같네요.
보통 컬링의 종류는 세가지가 있는데,
- 절두체 컬링 (Frustum Culling) - 카메라가 안보는 각도는 NO!
- 오클루전 컬링(Occlusion Culling) - 가린건 NO!
- 뒷면컬링(Backface Culling) - 뒷면은 NO!
그 중 지금 소개할 것은…
외적을 했으니 외적을 쓸 Backface Culling입니다.
말 그대로 뒷면을 그리지 않겠다! 라는 것입니다.
법선 (Normal) : 그래서 백페이스 컬링은?
그 전 삼각형의 정점부터 다시 봅시다.
2차원의 삼각형
여기서 정점에는 여러 정보가 들어가는데,
보통 위치, UV(텍스처 매핑을 위한 좌표), 탄젠트, 색상.. 등 여러정보가 들어가게 되는데, 그 중 노멀이라는게 들어가게 됩니다.
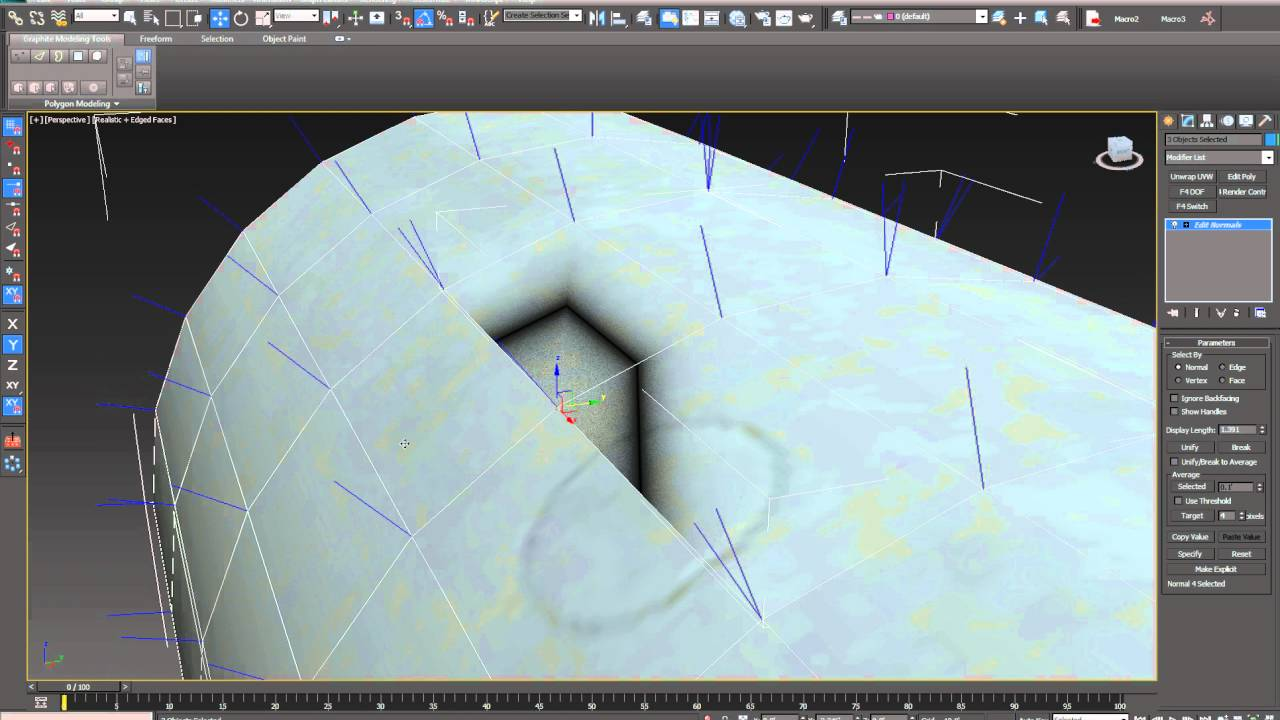
파란선분 : 3DsMax에서의 정점 법선(Vertex Normal)
그 정점의 평균값을 삼각형의 무게중심 좌표계를 통해 각 위치에 해당하는 노멀을 구할 수 있고, 이를 통해 곡선을 구할 수 있습니다 (참조 : NURBS)
하지만 면의 노말(faceNormal)은 조금 다릅니다.
각 버텍스의 노말을 따르지 않고, 버텍스의 위치를 기준으로 세 점을 통해 구한 두 벡터의 외적을 통한 노말입니다. (한마디로, 데이터는 줄이고 비슷하게 보인 짭이죠)

그러나 이 노멀은 결국 버텍스 의존적이라는게 문제입니다. (아마도요?)
그래서 나온것이 노말맵핑(Normal mapping)입니다.
R,G,B 세 값으로 XYZ 요소를 나눠, 어느방향으로 어떻게 요철이 형성되어있는가를 저장한 맵을 이용하여 요철을 표현합니다.

좌 - 실제 버텍스, 우 - 왼쪽의 메쉬로부터 연산된 맵을 이용한 평면 표면
아무튼 그렇게 적절한 버텍스와 적절한 텍스쳐를 통해 최상의 퀄리티를 뽑아낼 수 있는 노멀은 보통
스컬핑(sculpting)을 통해 정밀한 버텍스를 로우-폴리 모델에 구워낸다고 합니다.

아무튼 적절한 버텍스와 적절한 노말맵을 사용하여 최상의 가성비(…!)를 뽑아 내는것이 베스트인데요, 쉽게보자면 아래와 같습니다.
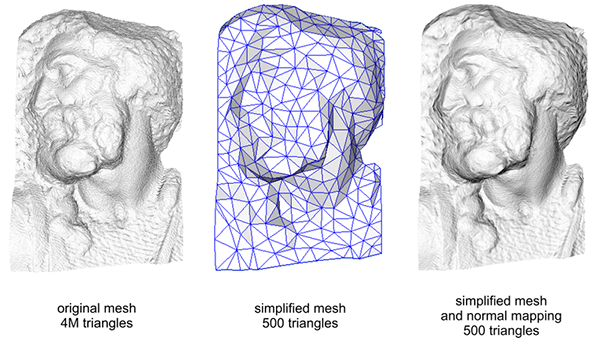
노멀맵(NormalMap)을 왜 사용하냐 물으면 자주 보이는 그림입니다.
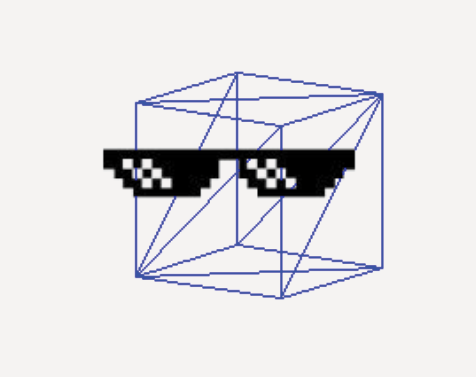
자 다시 돌아와서 여기서 이제 면의 노말을 기준으로 컬링을 해봅시다.
좌표계에 따라 인덱스버퍼에 정점 인덱스를 감기 시작한다면
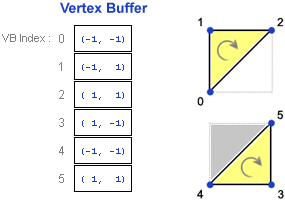
Direct3D9, Left Handed
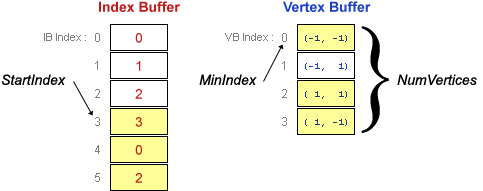
다음과 같이 됩니다.
이 세점을 통해 두 벡터를 구하고, 두 벡터의 외적을 통해 면의 노멀을 구합니다.
이 때, 카메라가 바라보는 방향과(오른손 좌표계의 forward라면, (0,0,-1)이겠죠?)
면의 노멀을 내적하여 0보다 작을 경우에만(즉 서로 마주보는 경우)
렌더링을 하도록 하는 겁니다.
그런데 잠깐. 꼭 내적을 해야할까요?
뷰 좌표계에서는 카메라의 시선방향이 (0,0,-1)입니다. (오른손 좌표계라면요.)
그러면 간단하게 내적도 필요 없이 을 검사하면 끝납니다!
와 참 쉬워요.
그러면 간단하게 비슷한 방법으로 구현할 수 있지 않을까요?
Fake Implementation : URP - Shader Graph
(당구표시) 주의! 시각적으로 뒷면을 날리는 방법을 ‘보여주는 것’이지, 실제 뒷면을 날리지 않습니다
요즘 쉐이더그래프를 만지작거리고 있어서 겸사겸사 해봤습니다.
뭐 있을건 다 있잖아요?
Two Side (양면렌더링) Lit 쉐이더를 하나 만들어 줍니다.
양면을 보여줘야 하니까 Transparent,
양면을 보여줘야 하니까 TwoSide.
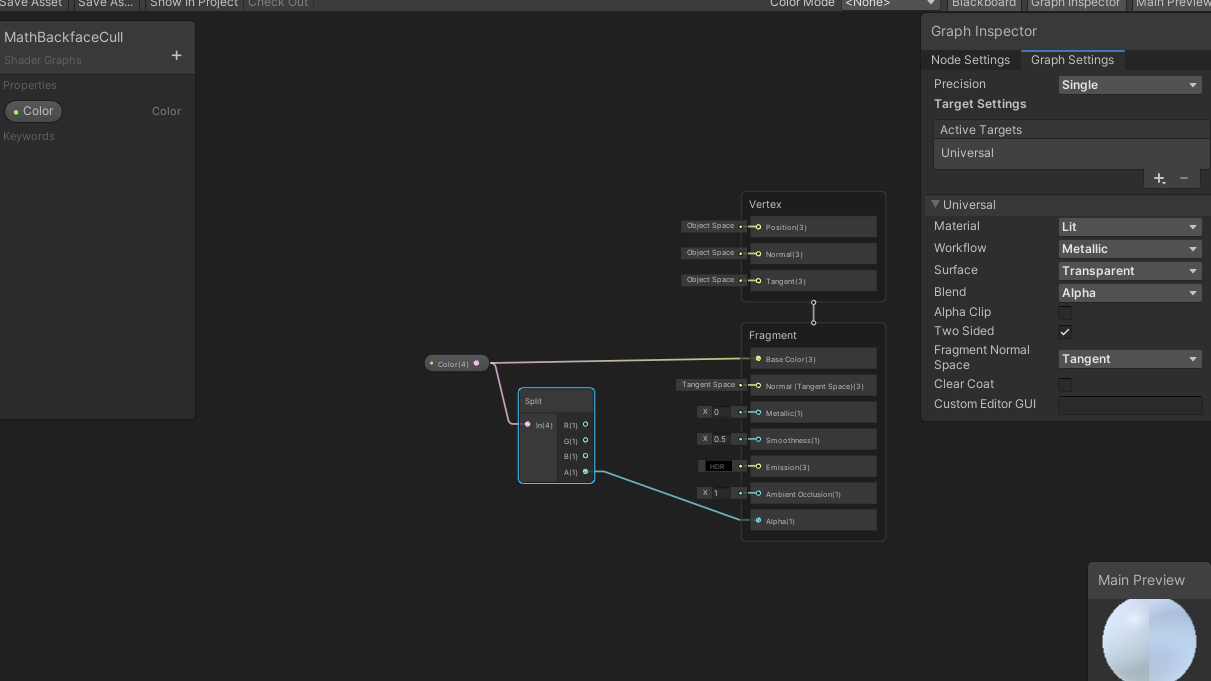
그럼 이런게 나옵니다.
색상이 저번주부터 왜 이러냐고요? 라이트 위치랑 색상이 제맘이라 그렇습니다.
그러면 이제 위에서 설명한대로 만들어 볼까요?
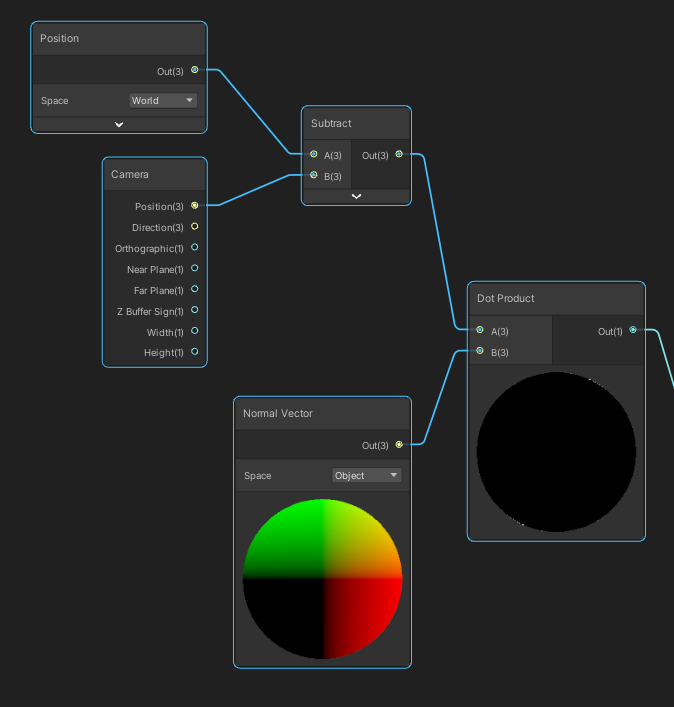
카메라에서 해당 면(여기서는 픽셀입니다)의 방향(Position - CameraPosition)과 노멀(Normal)을 내적합니다.
그리고 그 값이 0보다 작은 값들, 즉 마주보는 방향에 따라
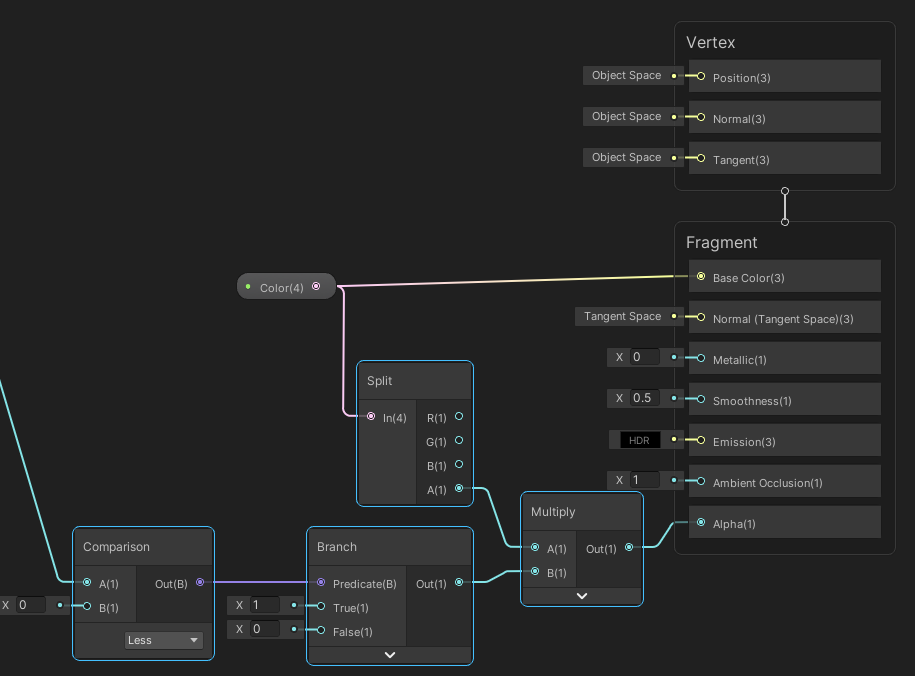
마주본다면 1, 그렇지 않다면 0의 값을 투명도에 곱합니다.
그러면 짠.

라이트 색상 좀 잘 받는 각도로 카메라를 옮겼습니다. 왜 색상이 기즈모를 안따르냐고요? 제 맘입니다.

지금은 시각적으로 보이지 않게 하기 위해 투명도를 0으로 설정하였지만,
실제 연산은 비교(Comparison)를 통해 얻은 값에 따라 렌더링 할지에 대한 여부를 고르면 됩니다.

위: URP lit Transparent alpha twoside 중간 : URP lit Transparent alpha front 아래 : 구현물
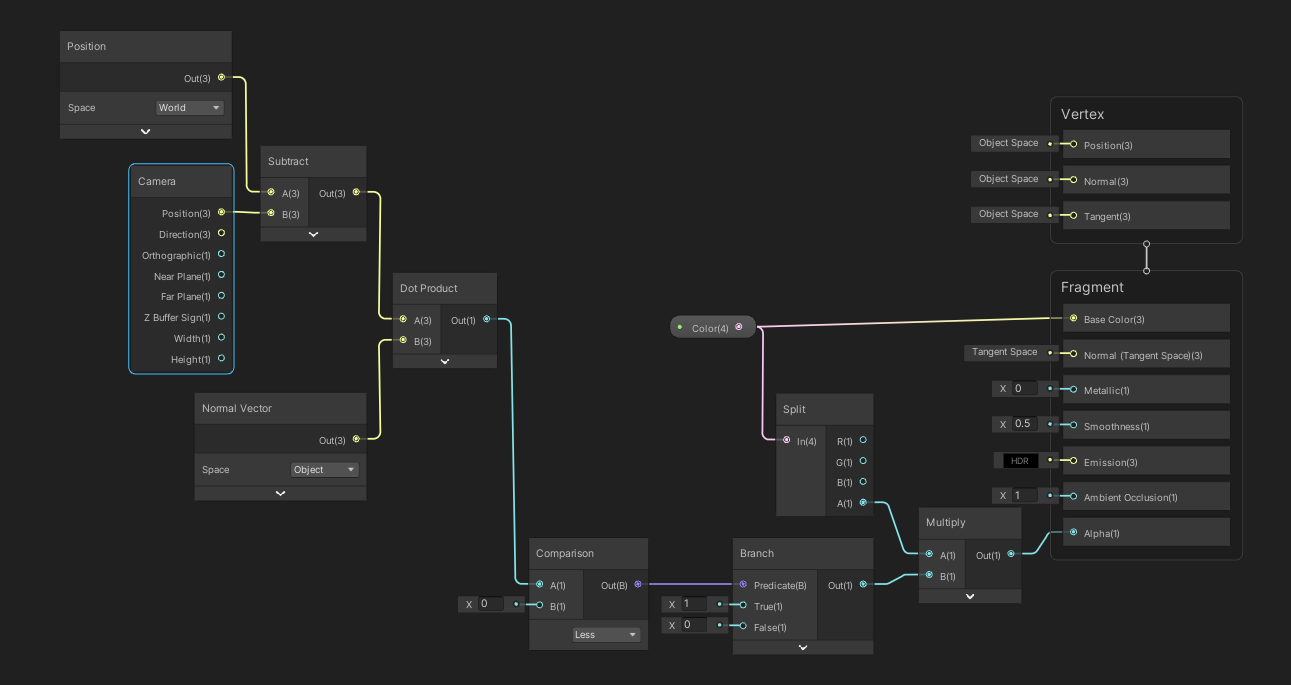
구현물
Implementation
자 그러면 엔진에 적용해봅시다.
별거없으니까 Gist 안쓰고 대충 적어보죠.
음수만 렌더링해야하니까 if문은 양수를 거릅니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// in SoftRenderer3D.cpp
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
auto& r = GetRenderer();
const GameEngine& g = Get3DGameEngine();
if (useBackfaceCulling)
{
// 백페이스 컬링 ( 뒷면이면 그리기 생략 )
Vector3 edge1 = (InVertices[1].Position - InVertices[0].Position).ToVector3();
Vector3 edge2 = (InVertices[2].Position - InVertices[0].Position).ToVector3();
Vector3 viewDirection = -Vector3::UnitZ;
if (edge1.Cross(edge2).Dot(viewDirection) >= 0)
return;
}
LinearColor finalColor = _WireframeColor;
if (InColor != LinearColor::Error)
{
finalColor = InColor;
}
r.DrawLine(InVertices[0].Position, InVertices[1].Position, finalColor);
r.DrawLine(InVertices[0].Position, InVertices[2].Position, finalColor);
r.DrawLine(InVertices[1].Position, InVertices[2].Position, finalColor);
}

완성
…
그런데 짜잔
1
2
3
4
5
6
7
8
9
10
11
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render3D()
{
...
Matrix4x4 finalMatrix = vMatrix * transform.GetModelingMatrix();
// 메시 그리기
DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());
...
}
}
최종 행렬식은 뷰 행렬이 적용되어있습니다!!!!!
수정합시다. 대신 뷰좌표계의 forward가 Z-이므로, 음수를 다 걸러줘야합니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
auto& r = GetRenderer();
const GameEngine& g = Get3DGameEngine();
if (useBackfaceCulling)
{
// 백페이스 컬링 ( 뒷면이면 그리기 생략 )
Vector3 edge1 = (InVertices[1].Position - InVertices[0].Position).ToVector3();
Vector3 edge2 = (InVertices[2].Position - InVertices[0].Position).ToVector3();
if (edge1.Cross(edge2).Z <= 0)
return;
}
LinearColor finalColor = _WireframeColor;
if (InColor != LinearColor::Error)
{
finalColor = InColor;
}
r.DrawLine(InVertices[0].Position, InVertices[1].Position, finalColor);
r.DrawLine(InVertices[0].Position, InVertices[2].Position, finalColor);
r.DrawLine(InVertices[1].Position, InVertices[2].Position, finalColor);
}
로드리게스 회전(Rodrigues rotation)
어느점에서 어느점까지면 그냥 하나축으로 돌려버리면 되는게 아닐까?! 하는 방법입니다.
이때까지 2축 이동을 선형보간하면 이상했었죠?
로드리게스 회전은 짐벌락도 없고 회전보간도 가능합니다.
…대신 너무 비쌉니다. 그리고 행렬변환도 어렵고 오일러각으로도 변환이 어렵습니다.
그림만 봐도 딱 각이 나오지 않나요?
저 축만 구하면 됩니다. 축은 어떻게 만들까요? 저 평면의 수직이니 외적을 하겠죠.
점 P로 향하는 벡터 u를 구합니다
점 빼기 점을 통해 구합니다.
Do you know Affine-space?
벡터 u를 벡터 n에 투영한 벡터 v을 구합니다
하지만 = 1,즉 단위벡터 이므로,
평면에서의 회전으로 확인합니다
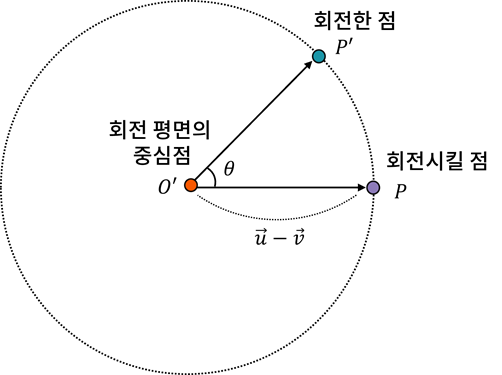
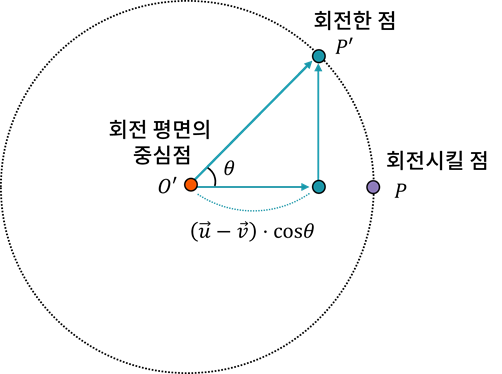
평면회전 많이해봤죠?
이 평면을 임시라고 생각하고, 이 평면에 해당하는 x,y축을 임시 x, 임시y축이라 합시다.
저 임시 x축의 값만 대충 생각해 둡시다.
임시 y축은… 현재상황에선 어떻게 구해낼 수 없으므로 3차원으로 도망쳐야합니다.
평면에서의 y축을 구합니다
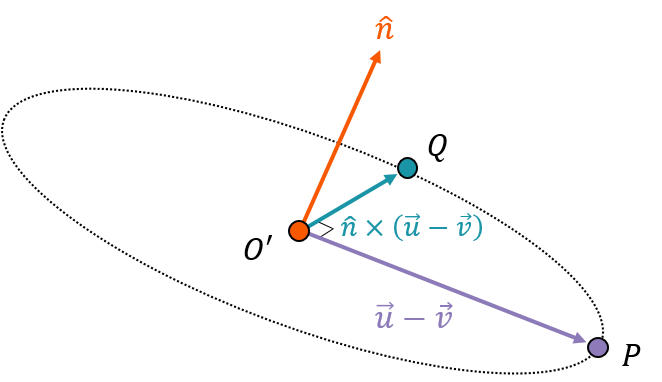
3차원으로 도망쳤으니, n벡터와 p로 가는 방향을 외적하여 임시Y축을 구합니다.
근데 저희는 오른손좌표계(외적순서말하는겁니다) 이니 n 를 해줍니다.
그러면 X축이랑 같이 해볼까요?
임시 XY축에 해당하는 값 다 구했죠?
식을 정리합니다
그러면 더하죠. 어쨋든 저희가 정해둔 임시XY축이든 뭐든
이 세상에는 3가지 기저밖에 없으니까요.
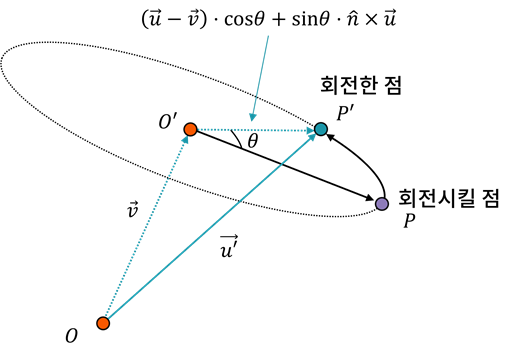
여기서는 가 누락되어 있으니, 의 변위 를 더해서
이걸 다시 한번 정리하면
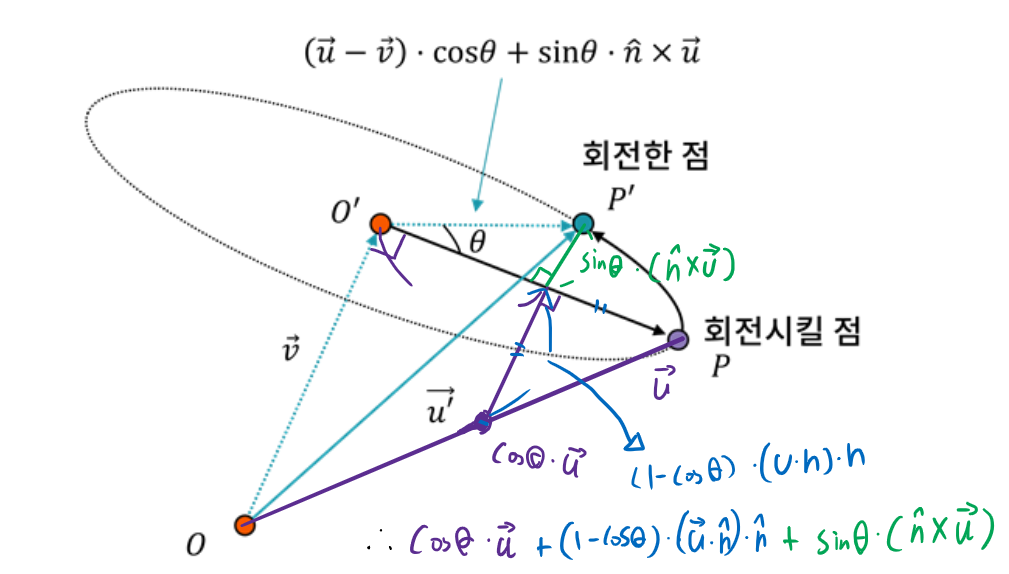
입니다.
맺으며
그렇게 저희는 오일러각의 문제를 해결하기 위해 외적과 잡다한걸 하면서 여기까지 왔습니다.
이것이 일반적인 벡터단위의 선형보간을 했을때의 문제입니다.
이걸 해결하기 위해… 저희는 배워야할 것이 많습니다.
마왕을 잡더라도 레벨1부터, 슬라임부터 시작해야죠.
그것이 수학이니까
하지만 저 로드리게스 회전공식은 안씁니다. 왜냐고요? 더 좋은게 있거든요.
하지만 외적을 다뤄보기엔 좋은문제였습니다.
https://twitter.com/book_quote_bot/status/1406297214973091846
Rmx.

