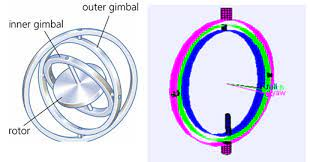
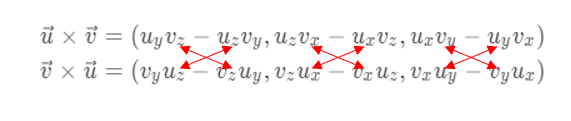Gimbal-Lock & Cross Product

서론

Untitled

일요일날 아파서 하루종일 곯아떨어졌더니 작성일이 밀릴뻔 했습니다.

오일러각의 문제

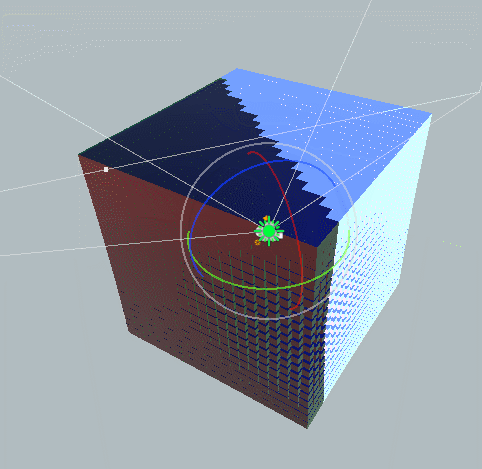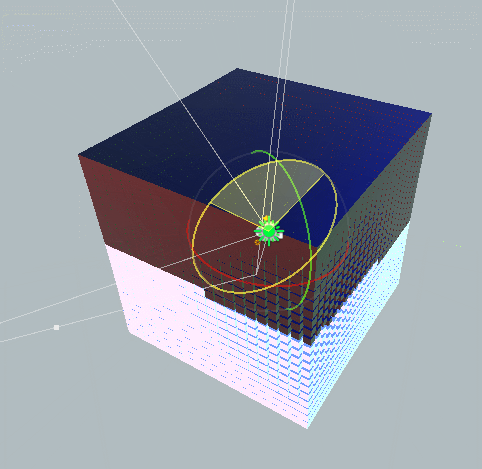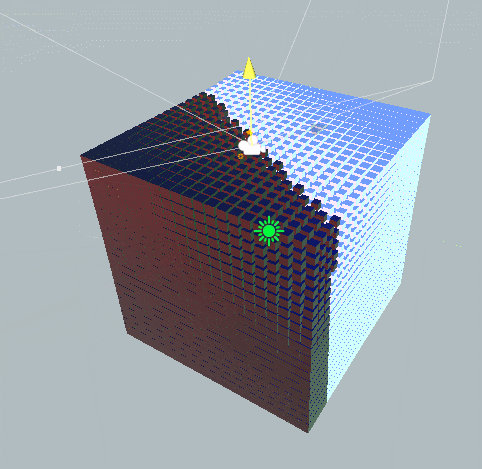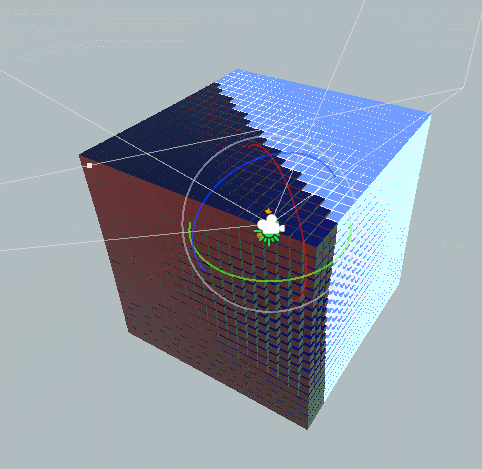
짐벌락(Gimbal-Lock)

Untitled

위의 이미지와 같이 특정 상황에서 두 축이 같은 회전을 수행하는 경우가 있습니다.

축이 잠겨버린(Lock)것이죠.

비슷한느낌을 보자면

https://youtu.be/k7RM-ot2NWY?t=224

같이 벡터가 한 선 위에서만 생성되는 느낌이라 볼 수 있습니다.

다시 짐벌락으로 돌아와서, 이렇게 두가지의 회전이 하나의 회전을 나타낼 때 보통

‘자유도(degree of freedom)가 떨어진다’ 라고 합니다.

회전의 보간

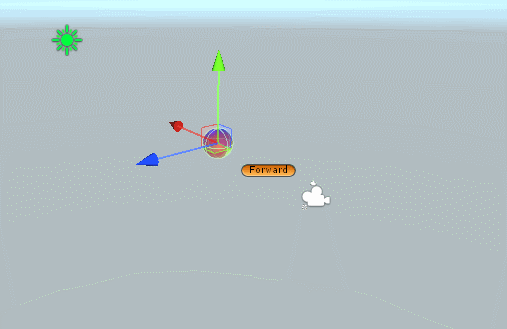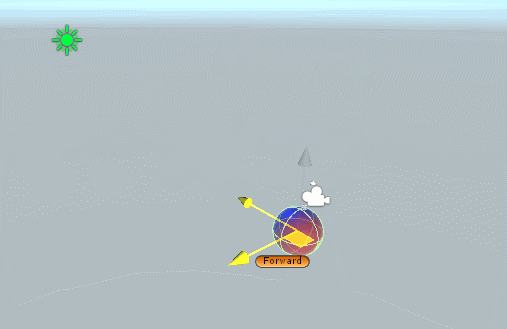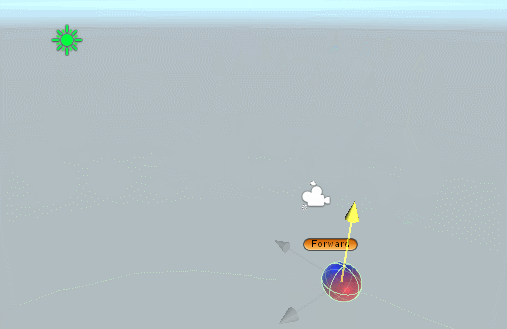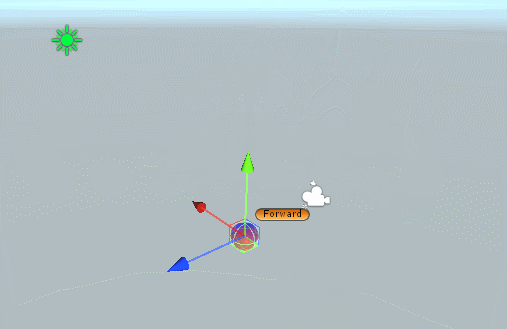
시작점과 끝점이 한축에만 사용할 경우엔 쉽게 보간이 가능합니다

하지만 두 축을 그대로 보간시 문제가 발생하죠.

예를들어 x축으로 180도, z축으로 180도 돌려보겠습니다.

결론적으로는 Y축으로 180도 회전한 것이지만, 회전의 보간 각도를 보면 위로 올라갔다가 내려오는 부자연스러운 꼴을 하고 있습니다.

이것이 일반적인 벡터단위의 선형보간을 했을때의 문제입니다.

이걸 해결하기 위해… 저희는 배워야할 것이 많습니다.

마왕을 잡더라도 레벨1부터, 슬라임부터 시작해야죠.

그것이 수학이니까

벡터의 외적(Cross Product)

벡터의 외적 기초

외적/외곱/벡터적/벡터곱 (Cross Product, Vector Product, Outer Product) ⇒ 임의 두 벡터로부터 또다른 벡터량을 생성해내는 연산

정의

Definition
$\vec{u} \times \vec{v} = \vert \vec{u}\vert \space \vert \vec{v}\vert \space sin \theta \space \vec{normal} = \vec{w}$
$\vert \vec{u}\vert$ , $\vert \vec{v}\vert$ = 벡터 $\vec{u},\vec{v}$ 의 크기
$\vec{normal}$ = 두 벡터 $\vec{u},\vec{v}$ 의 수직(좌표계에 따름) 방향
$\theta$ = $\vec{u},\vec{v}$ 가 이루는 각의 크기

외적의 수식과 특징

\vec{u} \times \vec{v} = \vec{w}

외적(cross product)는 3차원에서 밖에 성립이 안되는 연산입니다.

그리고 연산자의 명칭은 Times( $\times$ ), u cross v 라고 읽습니다.

연산을 정리하자면

\vec{u}=\left(u_x,\ u_y,\ u_z\right),\ \vec{v}=\left(v_x,\ v_y,\ v_z\right) \\ \vec{u}\times\vec{v}= \left(u_yv_z-v_yu_z,\ u_zv_x-v_zu_x,\ u_xv_y-v_xu_y\right) = \vec{w}

와 같이 나타낼 수 있습니다.

또한 보통 외적 연산은

x→y→z→x→y→z→….
yz→yz→zx→xy→yz→….
(yz-zy, zx-xz, xy-yx) & uv

와 같은 순서로 연상하면 쉽게 됩니다.

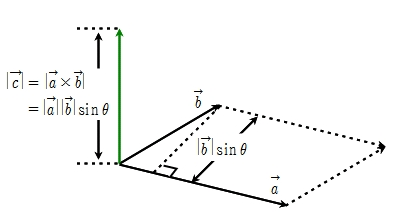
외적을 크게 크기와 방향으로 나뉘어서 생각한다면,

이때 외적한 결과 $\vec{w}$ 의 크기는 평행사변형의 넓이 공식 $(\vert \vec{v}\vert \vert \vec{u}\vert sin(\theta))$ 를 따라갑니다

그리고 $\vec{normal}$ 은 두 벡터에 수직인 벡터입니다.

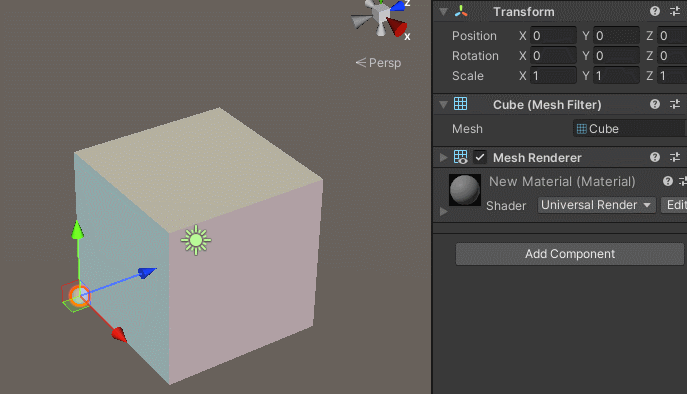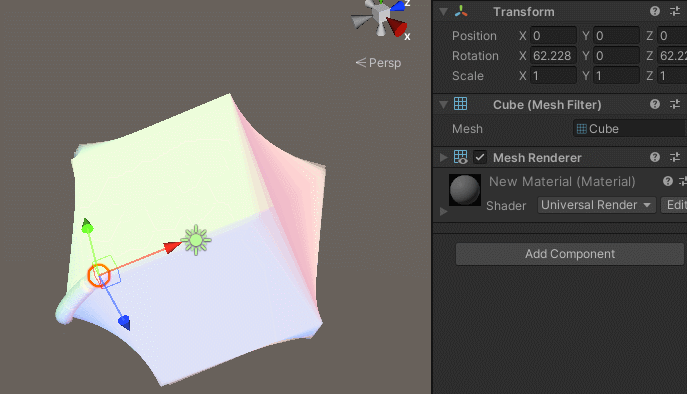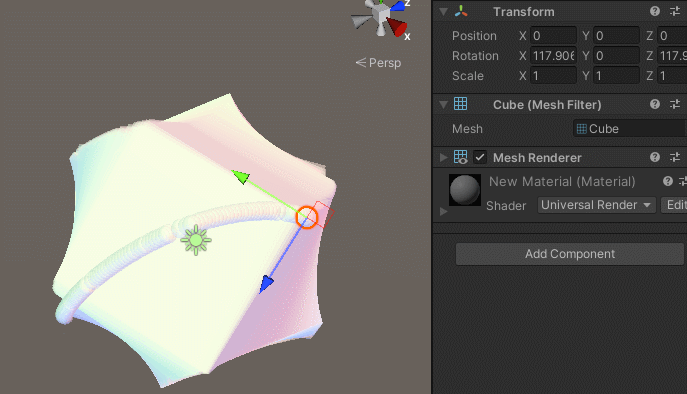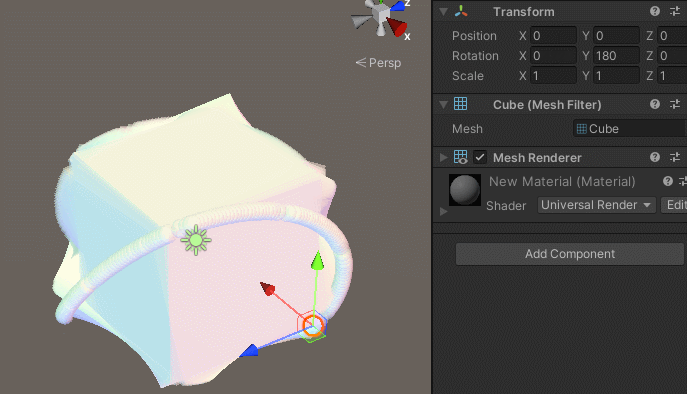
시각화 해볼까요?

Untitled

잠깐, 여기서 $sin(\theta)$ 를 잘 본다면,

사잇각 $\theta$ 에 비례하여 크기가 결정된다는 것을 알 수 있습니다.

외적 연산의 성질

대부분의 연산이 뺄셈과 관련이 있다는 것을 생각하면 쉽게 나올 수 있습니다.

기본적인 성질

교환법칙\\ \vec{u} \times \vec{v} =(u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)\\\vec{v} \times \vec{u} =(v_yu_z-v_zu_y,v_zu_x-v_xu_z,v_xu_y-v_yu_x)\\=(u_zv_y-u_yv_z,u_xv_z-u_zv_x,u_yv_x-u_xv_y)

어라 그런데 여기 재미있는게 있습니다. 하지만 여백이 부족하니 나중에 적겠습니다.

$\therefore$ 교환(commutativity) : 비성립 , $\vec{u}\times\vec{v}\neq\vec{v}\times\vec{u}$

\vec{u} \times (\vec{v} \times \vec{w} )= \vec{u} \times (v_yw_z-v_zw_y, v_zw_x-v_xw_z, v_xw_y-v_yw_x)\\ = (u_y(v_xw_y-v_yw_x) - u_z(v_zw_x-v_xw_z),\\ u_z(v_yw_z-v_zw_y) - u_x(v_xw_y-v_yw_x),\\ u_x(v_zw_x-v_xw_z) - u_y(v_yw_z-v_zw_y))

(\vec{u} \times \vec{v} )\times \vec{w}=(u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)\times \vec{w}\\=((u_zv_x-u_xv_z) w_z - (u_xv_y-u_yv_x) w_y,\\(u_xv_y-u_yv_x) w_x - (u_yv_z-u_zv_y) w_z,\\(u_yv_z-u_zv_y) w_y - (u_zv_x-u_xv_z) w_x)

$\therefore$ 결합(associativity) : 비성립 , $\vec{u}\times\left(\vec{v}\times\vec{w}\right)\neq\left(\vec{u}\times\vec{v}\right)\times\vec{w}$

...대충그런갑다 해주세요

…대충그런갑다 해주세요

덧셈에 대한 외적 연산의 분배법칙(distributivity) : 성립 $\vec{u}\times\left(\vec{v}+\vec{w}\right)=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}$

…

다시한번 잠깐 교환법칙을 보겠습니다
$\vec{u} \times \vec{v} =(u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)\\\vec{v} \times \vec{u} =(v_yu_z-v_zu_y,v_zu_x-v_xu_z,v_xu_y-v_yu_x)\\$

어라라? 뭔가 뭔ㄴ가…!

Untitled

그렇습니다.

\vec{u} \times \vec{v} =(u_yv_z-u_zv_y,u_zv_x-u_xv_z,u_xv_y-u_yv_x)\\ \vec{-v} \times \vec{u} =(-v_yu_z-(-v_zu_y),-v_zu_x-(-v_xu_z),-v_xu_y-(-v_yu_x))\\ =(v_zu_y-v_yu_z,v_xu_z-v_zu_x,v_yu_x-v_xu_y)

그렇다면 곱셈에 대한 교환법칙이 성립하므로, 두 식은 일치한다고 볼 수 있습니다.

$\therefore$ 반수 성질 : $\vec{u}\times\vec{v}=-\vec{v}\times\vec{u} \\$

평행성

$\vec{u} \times \vec{v} = \vert \vec{u}\vert \space \vert \vec{v}\vert \space sin \theta \space \vec{n} = \vec{w}$

에서 외적의 식에 따라, $sin(\theta)$ = 0 일 때 혹은 $\vert \vec{u}\vert =0,\vert \vec{v}\vert =0$ 일때 $\vec{w} = \vec{0}$

두 벡터가 평행일 필요충분조건은 $\vec{u}\times\vec{v} = \vec{0}$ 이므로

$\therefore$ 두 벡터를 외적해서 0나오면 평행입니다.

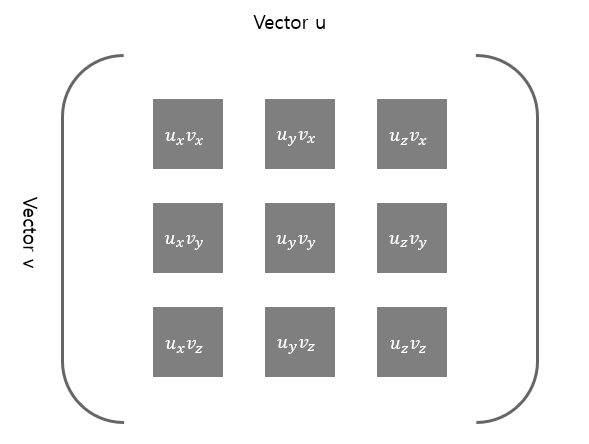
외적과 내적의 비교

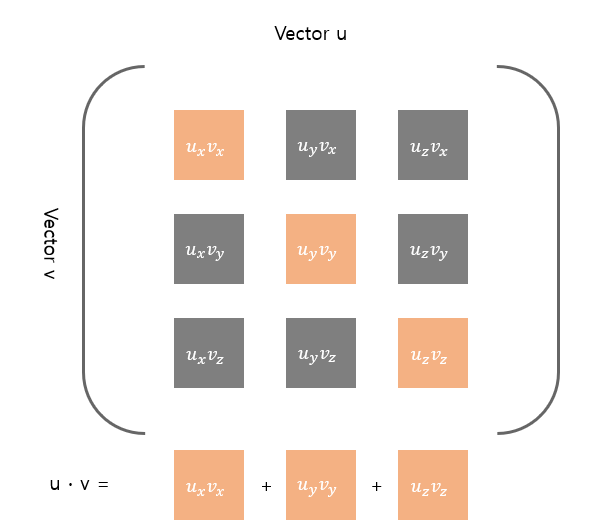
Untitled

두 벡터의 성분 곱을 위와 같이 표현하였을 때 ,

내적의 경우는

Untitled

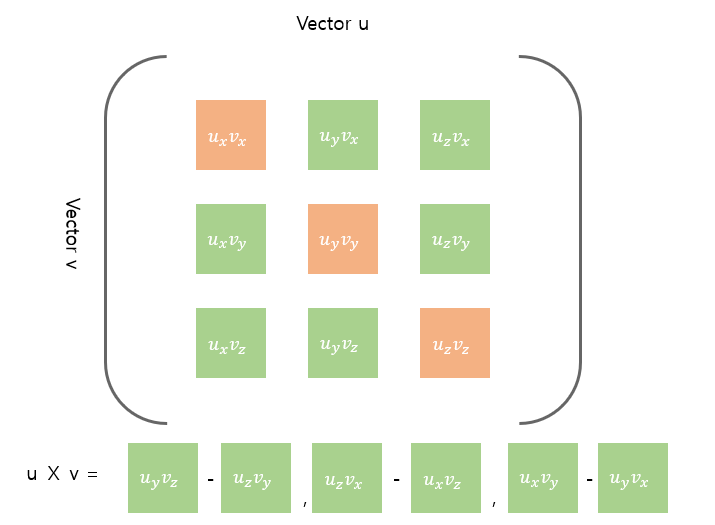
외적의 경우는

Untitled

과 같습니다. 상호 보완관계죠

어..어라 이게 아닌가요?

하지만 여기서 더 보다보면 재미있는 것들이 나옵니다.

저번 소행렬식을 구하는 것과, 오일러각 행렬을 생각해보면 유사성을 볼 수 있죠 (3x3 행렬에서 뭐 다 비슷하긴 하겠지만요)

두 벡터 $\vec{u} , \vec{v}$ 의 각 원소 곱을 다음과 같이 표시할 때,

각 ( $u_xv_x,u_yv_y,u_zv_z$ )를 제외한 소행렬식의 연관관계로 표시해보면

다음과 같습니다. (눈이 침침해서 회색과 검정의 차이가 잘 안보입니다)

예를 들어 $a$ 를 소거할 경우 $\vec{u} = (b,e,h),\vec{v} = (c,f,i)$ 로 본다면,

\left[ \begin{matrix} \color{gray}a&\color{gray}b&\color{gray}c\\ \color{gray}d&e&f\\ \color{gray}g&h&i\\ \end{matrix} \right] \left[\begin{matrix}a&\color{gray}b&c\\\color{gray}d&\color{gray}e&\color{gray}f\\g&\color{gray}h&i\\\end{matrix}\right] \left[\begin{matrix}a&b&\color{gray}c\\d&e&\color{gray}f\\\color{gray}g&\color{gray}h&\color{gray}i\\\end{matrix}\right] \\ \rightarrow \vec{w} (ei-fh,-(ai-gc),ae-bd)

참 재미있지 않나요?하하 det를 구할 때, $S_{ij}$ 를 취한 것과 또 유사한 식이 나오는 군요.

\sum_{j=1}^{n} (-1)^{i+j}\cdot a_{ij} \cdot det(S_{ij})

그리고 회전 행렬때는

$Roll = Rot_z= \left[ \begin{matrix} cos{\theta}&-sin{\theta}&0\\ sin{\theta}&cos{\theta}&0\\ 0&0&1\\ \end{matrix} \right]$
xy평면을 기준으로 x to y 회전을 표현합니다.
$Pitch = Rot_x= \left[ \begin{matrix} 1&0&0\\ 0&cos{\theta}&-sin{\theta}\\ 0&sin{\theta}&cos{\theta}\\ \end{matrix} \right]$
yz평면을 기준으로 y to z 회전을 표현합니다.
$Yaw = Rot_y= \left[ \begin{matrix} cos{\theta}&0&sin{\theta}\\ 0&1&0\\ -sin{\theta}&0&cos{\theta}\\ \end{matrix} \right]$

와 같이 처리하였었죠.

뭔가 다 비슷비슷하게 생겼어요! 관련이있을지도? (그런데 3x3행렬에서 뭔가 할려하면 다 그런거겠죠 뭐)

외적 연산 및 내적 연산의 성질 비교

내적

결합법칙 - 성립하지 않습니다
교환법칙 - 성립합니다
덧셈에 대한 분배 - 성립합니다
연산에 코사인이 첨가됨

외적

결합법칙 - 성립하지 않습니다
교환법칙 - 성립하지 않습니다
덧셈에 대한 분배 - 성립합니다.
연산에 사인이 첨가됨

임의의 두 벡터에 대한 외적

\vec{u}=\left(u_x,\ u_y,\ u_z\right),\ \vec{v}=\left(v_x,\ v_y,\ v_z\right) \\\vec{u}\times\vec{v}=\left(u_yv_z-v_yu_z,\ u_zv_x-v_zu_x,\ u_xv_y-v_xu_y\right) \\\vec{u}\cdot\left(\vec{u}\times\vec{v}\right)=u_xu_yv_z-u_xv_yu_z+u_yu_zv_x-u_yv_zu_x+u_zu_xv_y-u_zv_xu_y = \vec{0}\\ \vec{v}\cdot\left(\vec{u}\times\vec{v}\right)=v_xu_yv_z-v_xv_yu_z+v_yu_zv_x-v_yv_zu_x+v_zu_xv_y-v_zv_xu_y = \vec{0}

$\vec{u},\vec{v}$ 에 대해 직교한다.

즉 두 벡터로 만들 수 있는 공간에 직교하는 벡터가 만들어집니다.

물론 방향은 좌표계를 따릅니다.

벡터 외적의 활용

좌우판별

바라보는 방향과 물체의 방향을 외적한 값은 upVector와 평행한 벡터가 나오게 되는데,

이를 설정하여 내적하여 유사도를 구한 다음, 그 값의 부호로 판별하는 방법입니다.

카메라의 업벡터를 통해 좌(subtractive)와 우(additive) 의 색상이 변경됩니다.

2차원으로 구성할까 하다가 UP벡터 역시 변할 수 있다고 생각하여 카메라의 로컬 UP을 사용하였습니다.

그리고 외적의 크기값을 스케일로 치환하여 한번 만들어 보았습니다.

정규화 하지않은 벡터를 사용하였고,

0벡터일 때 최소이므로, 가깝거나 시야와 평행이 될수록 작아집니다.

외적을 활용한 시선벡터로부터의 회전행렬

카메라의 기저축

시선벡터 $\vec{u}$ , Up벡터를 $\vec{v}$ 라고 가정할 때,

가장 쉬운것 부터 구해봅시다.

$\vec{z}$ 는 당연하게도 $\vec{u}$ 이므로, 기저를 구하기 위해 정규화(normalize)합니다

\vec{z} = \frac{\vec{u}}{\vert \vec{u}\vert }

$\vec{x}$ 는 이제 시선벡터 $\vec{u}$ 와 아까 가정한 $\vec{v}$ 를 외적한 값을 정규화합니다.

0벡터가 아닌, 평행하지 않은 두 벡터가 있다면 나머지 한 수직축을 구할 수 있으니까요

\vec{x} = \frac{\vec{u} \times \vec{v}}{\vert \vec{u} \times \vec{v}\vert }

0벡터가 아닌, 평행하지 않은 두 벡터가 있다면 나머지 한 수직축을 구할 수 있으니,

$\vec{y}$ 는 아주 간단하게도 두 정규화된 벡터를 외적하면 됩니다.

\vec{y} = \vec{z} \times \vec{x}

정규화는 안하냐구요?

외적의 크기는? 두 벡터로 만들어지는 평행사변형의 넓이이자 det과 유사하므로, 둘의 크기가 1이고 둘이 직교한다면 어쩔수없이 1일 수 밖에 없기 때문이죠.

LookAt 구현

그런데잠깐. 어짜피 해당 벡터는 오일러각도 아니고 어떻게 넣어야할까요?

그저 세개의 기저벡터일 뿐인데…

잠깐… 기저벡터…..?

M=\left[\begin{matrix} x_x&y_x&z_x&0\\ x_y&y_y&z_y&0\\ x_z&y_z&z_z&0\\ 0&0&0&1\\ \end{matrix}\right]

연산할 필요가 없습니다 야호!

Implementation

  
private void LookAt(in Transform origin, in Vector3 target)
{
    var u = target - origin.position;
    var v = Vector3.up;

    var local_axis_z = u.normalized;
    var local_axis_x = Vector3.Cross(u, v).normalized;
    var local_axis_y = Vector3.Cross(local_axis_z, local_axis_x);

    Matrix4x4 mat = new Matrix4x4()
    {
        m00 = local_axis_x.x ,m01 = local_axis_y.x, m02 = local_axis_z.x, m03 = 0,
        m10 = local_axis_x.y ,m11 = local_axis_y.y, m12 = local_axis_z.y, m13 = 0,
        m20 = local_axis_x.z ,m21 = local_axis_y.z, m22 = local_axis_z.z, m23 = 0,
        m30 = 0              ,m31 = 0             , m32 = 0             , m33 = 1
    };

    origin.rotation = mat.rotation;
}

호오 그러나 카메라가 뒤집혀버리고 맙니다..

당연합니다. 좌표계가 다르기 때문입니다.

저희가 계산할 땐 z+와 y+를 외적하면 x+가 나왔지만(오른손좌표계)

유니티(왼손좌표계)에서는 x-가, 그러면 이제z+와 x-를 외적하면 y-가 나오게 됩니다.

그럼 뭐 Up대신 Down을 사용하거나…

x축 구할때 $\vec{v} \times \vec{u}$ 를 하면 되겠죠.

Untitled

Rmx.

맺으며

예전에 행렬의 det은… 생각해보니 설명하지 않았지만 두 기저 벡터로 만들어진 마름모의 넓이 비슷한 말을 한 적 있습니다.

그러면 3차원 행렬의 det은 무엇일까요? 세 기저벡터로 만들어진 부피가 아닐까요?

3차원의 행렬식은 a(ei-fh)-b(di-fg)+c(dh-eg) 입니다.

그러면 여기서 2차원의 행렬식 ac-bd를 나눈한 값이 높이, 즉 외적의 크기가 되는게 아닐까요?

아몰랑 일단 식개조나 해봅시다

det은 전치해도 같은값 (det( $A^T$ ) = det( $A$ ))이 나오니 일단 보기편하게 뒤집읍시다.

M=\left[ \begin{matrix}a&b&c\\d&e&f\\g&h&i\\\end{matrix}\right],M^T = \left[\begin{matrix}a&d&g\\b&e&h\\c&f&i\\\end{matrix}\right]

def,ghi는 저희가 익숙한 두 기저벡터 $\vec{u}, \vec{v}$ 를 넣어줍니다

M = \left[\begin{matrix}a&b&c\\u_x&u_y&u_z\\v_x&v_y&v_z\\\end{matrix}\right] M^T = \left[\begin{matrix} a&u_x&v_x\\b&u_y&v_y\\c&u_z&v_z\\ \end{matrix}\right]

그러면 3차원의 행렬식은 $a(u_yv_z-v_yu_z) + b( u_zv_x-v_zu_x)+c(u_xv_y-v_xu_y)$ 입니다. ( $b$ 는 부호를 뒤집었습니다)

이게…뭘까요………….

뭔가 잡힐듯 말듯한게 아직은 때가 아닌듯 싶습니다.

2. Gimbal-Lock & Cross Product

서론

오일러각의 문제

짐벌락(Gimbal-Lock)

회전의 보간

벡터의 외적(Cross Product)

벡터의 외적 기초

정의

외적의 수식과 특징

외적 연산의 성질

외적과 내적의 비교

외적 연산 및 내적 연산의 성질 비교

임의의 두 벡터에 대한 외적

벡터 외적의 활용

좌우판별

외적을 활용한 시선벡터로부터의 회전행렬

카메라의 기저축

LookAt 구현

Implementation

맺으며

Further Reading

1. 3D Transform

3.Backface Culling & Rodrigues rotation

4.Triple Product & Perspective Projection