함수! 수학보단 프로그래밍에 익숙한 그 단어가 나왔습니다.

함수의 정의

함수는 한 집합의 원소들을 다른 집합의 원소들에 대응하는 규칙입니다.

다르게 말하자면 두 집합간의 대응 관계(relation) 라고도 볼 수 있죠.

표기할 때는 이렇게 표기합니다

$f:A\to B$
$A$ 를 $B$ 로 매핑하는 함수 f

일단 함수를 알기 위해서는 가장 작게 함수만을 들어낼 수 있는 유닛으로 바꿔보죠.

함수는 총 세개의 영역으로 볼 수 있습니다.

정의역(Domain) : 함수의 값이 ‘정의된’ 집합
공역(Codomain) : 함수의 값이 ‘속하는’ 집합
치역(Range) : 함수의 ‘출력’의 집합

함수의 필수조건

여기서 제일 중요한 필수 조건은

정의역의 원소는 공역의 원소에 대응합니다.
해당 대응은 ‘유일(unique)’해야 합니다. ( x → b 이며 동시에 x → c 는 안됩니다)

이렇게 본다면 정의역과 공역에 대해 치역에 대응하는,

이항대응(binary relation)이라 볼 수 있습니다.

이제 이 영역을 통해 하는 매핑을 알아보죠.

Mapping은 한국어로 참 많은 비슷한 단어들이 있습니다.

사상,변환,매핑,함수,연산,투영… 그 중 선형대수학에서는 ‘변환’을, 기하학에서는 ‘사상’,’변환’,’투영’ 을 주로 씁니다.

그런데 중간에 함수가 끼여있죠? 함수도 매핑중 더 좁은 범위를 뜻하는 말입니다.

그러면 함수는 무엇인가? 多:1 혹은 1:1과 같이 1개의 결과만을 내놓을 때, 혹은 수→수 로 가는 경우를 말합니다.

정의역, 공역, 치역, 입력, 출력 …

말을 정정해서 이제 이 정의역과 공역, 치역을 통해 행해지는 함수를 뜯어봅시다.

정의역(domain)에서 인자(argument)를 선택하여 입력(input)합니다.
내부에서 함수의 정의에 따라 무언갈 합니다.
최종적으로 산출된 변수(variable)이 출력(output)됩니다.
출력이 나올 수 있는 가능성이 있는 범위인 공역(codomain) 내의 해당 출력(output)은 치역(Range)에 속합니다.
- 이때 인자(argument) 및 출력값은 모두 변할 수 있으므로 변수(variable)입니다.
- 영향을 받지 않는 내부값은 상수(const)입니다.

  
int Function(int arg1,int arg2)
{
	int result;
	//뭔가 일어나고 있음
	//어쨋거나 저쨋거나 결과를 result에 담음
	return result;
}

//여기서 arg1, arg2가 입력(input)이며 인자(argument)입니다. 동시에 변할 수 있으니 변수입니다.
//result는 출력(output)이며, 인자(argument)에 따라 변화하니 변수입니다.

함수의 종류

대응되는 두 집합의 원소간의 관계(relation)에 따른 구분

전사(Surjection) : 공역과 치역이 동일

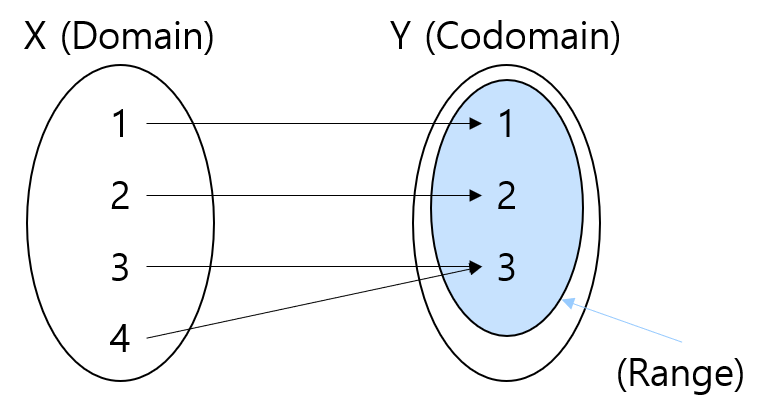
2%20Function%20&%20Vector%207a85d14a3b7846a8bafa4030dec63f9e/1.png

단사(Injection) : 정의역과 공역이 1대1로 대응

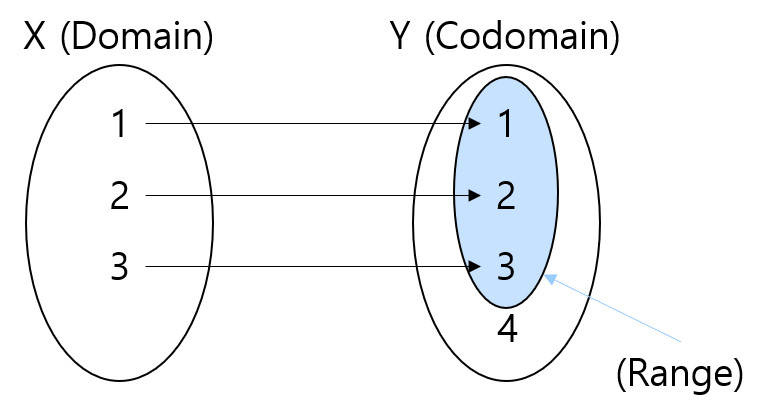
2%20Function%20&%20Vector%207a85d14a3b7846a8bafa4030dec63f9e/2.png

전단사(Bijection) : 전사와 단사를 모두 만족

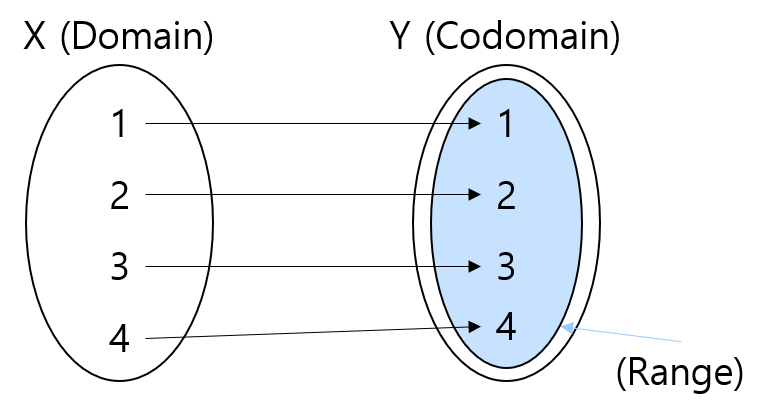
2%20Function%20&%20Vector%207a85d14a3b7846a8bafa4030dec63f9e/3.png

그러면 이제 이걸 기반으로 예시코드를 써봅시다!

대신 조건이 좀 물려있지만… 1주차의 상속관계가 아니라 ‘함수’니까 ‘함수’처럼 작성해 보죠.

  
int Function(float v)
{
	if(...)
		return 1;
	else
		return 0;
}

//함수 Function에 대해 
//parameter v에 대해 float = 실수(R)은 domain이라 한다.
//반환형인 int = 정수(Z)는 codomain, 반환값 {0,1}은 Range이다.

//전사 - surjection
//편의상 bool을 GF(2)로, 0=false, 1=true로 가정하겠습니다.
bool Function(int v)
{
	if(v<10)
		return true;
	else
		return false;
}

//단사 - injection
int Function(int v)
{
	return v * 2;
}
// codomain의 홀수(odd)의 값은 대응되지 않으며, 
//domain과 codomain의 요소가 1대1로 대응함

//전단사 - Bijection
bool Function(bool v)
{
	return !v;
}
//모든 원소가 1대1로 대응하며, 
//domain 과 codomain의 요소가 1대1로 대응하며, 
//codomain과 range가 같음

그런데 전단사의 함수를 작성하다가 이런생각을 했습니다.

만약 $\mathbb {Z} \to \mathbb {Z} }, {\displaystyle n\mapsto n+1$ 의 경우 각각 무한하지만 서로 1이라는 차이가 있고, 1대1 대응을 하는데 이는 전단사일까요?

궁금해서 물어보니 N번방 호텔 이야기인가요? 라는 말을 들었습니다.

역시 똑똑한사람들이 이런것도 미리 다 생각을 했었나 봅니다.

참조 : 힐베르트의 호텔 : https://youtu.be/Uj3_KqkI9Zo

근데 이걸 안보고 생각부터 해봤습니다. 생각을 해야 뇌가 말랑말랑해지죠.

생각 끝에 내린 결론은 『NO』였습니다. 생각은 대충 이러하게 진행했습니다.

러프하게 생각했기때문에 논리적으로 모순이 있을 수 있지만. 적어보겠습니다.

자연수 $\mathbb N$ 에 대해

  
int Func(uint x)
{
	if(x%2 ==0)
		return x/2;
	else
		return -(x-1)/2
}

라는 함수를 적용했다고 가정합시다.

아참, 수학으로 이런 함수를 적는법을 몰라서 코드로 적었습니다.

뭐 논리적으로 말되면 이것도 저것도 오케이겠죠. (오버플로우요? $\mathbb N$ 은 무한합니다)

그러면 $f:\mathbb N→\mathbb Z$ 이 됩니다. 양측이 무한하니 결국 언젠간 빈틈없이 매핑이 다 되겠죠.

그렇다면, 역의 경우도 작성할 수 있다고 생각합니다.

이제 $\mathbb {N}$ 에서, 가장 작은 $\mathbb {N}$ 의 원소인 $1$ 은 $1\mapsto 1+1$ 이므로 codomain에서 $1$ 이 대응되지 않습니다.

그러면 $\mathbb Z$ 에 대해, 가장 작은 $\mathbb {Z}$ 의 원소인 $e$ 은 $e\mapsto e+1$ 이므로 codomain에서 $e$ 가 대응되지 않을 것입니다.

물론 무한의 개념에서 이게 과연 옳은 생각인가 생각이 들긴 하지만…

저는 수학자가 아니므로 모르겠습니다.

심지어 이렇게 답을 찾는 방식도 일반적인 프로그래밍에서 테스트하는

엣지케이스 방식으로 생각하다 찾았습니다

( $\mathbb Z$ 는 양쪽으로 무한이니까 $\mathbb N$ 으로 변환한 다음에 닫힌부분의 끝을 보면 되는게 아닐까?)

아무튼 그렇게 뭔가 옆으로 좀 샌 것 같지만 함수의 종류를 정리해봤습니다.

곱집합에 대한 정리, 이항연산을 함수로 표현

곱 집합(Product Set)

두 집합 $A,B$ 의 원소들로 만들어지는 모든 순서쌍 $(a,b)$ 의 집합

다른말로는 카테시안/데카트르 곱(cartesian Product)이라고도 합니다.

여기서 순서쌍 $(a,b)$ 로 표현하는걸 튜플(tuple)이라 합니다

튜플(tuple)은 쉽게 설명하면 셀 수 있는 수량의 순서가 있는 열거입니다.

코드에서도 간단하게 쓸때 좀 쓰긴 하죠.

  
//여기서 List<T>의 T가 tuple입니다.
void LogError(List<(bool,int,string)> logs)
{
	foreach(var log in logs)
	{
		if(log.item1)
		{
			var message = $$"Error code : {log.item2} , {log.item3}";
			Logger.Log(message);
		}
	}
}

그러면 카테시안 곱의 표기는 어떻게할까요?

카테시안 곱의 표기는 $A \times B$ 로표기합니다

$A \times B = \{(a,b) \enspace | \enspace a \isin A \enspace and \enspace b\isin B\}$

곱집합은 예를 들면 어떤게 있을까요?

같은 특성의 곱으로 유명한건 직교좌표계(데카르트 좌표계, cartesian coordinate system)입니다.

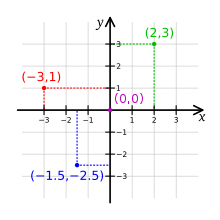
2%20Function%20&%20Vector%207a85d14a3b7846a8bafa4030dec63f9e/Untitled.png

자주 보아왔던 이런 직교좌표계는 $\mathbb R^2$ , 즉 $\mathbb R$ 과 $\mathbb R$ 의 곱집합입니다.

그리고 이건 좀 있다가 다시 다루겠습니다.

왜냐하면 이건 말할게 따로 있습니다.

같은 집합이 아닌 곱으로 만들어진건 무엇이 있을까요?

트럼프카드가 그 예입니다.

트럼프카드의 경우 문양집합(♠,♥,♦,♣) 및 수 집합(A,2,3,4,5,6,7,8,9,10,J,Q,K)의 곱입니다

좌표평면에 대응하자면 x축 방향으로 수 집합을, y축방향으로 문양집합을 대응할 경우

2%20Function%20&%20Vector%207a85d14a3b7846a8bafa4030dec63f9e/Untitled%201.png

다음과 같은 꼴이 되겠죠.

읽는 법은 예를들어 ♠ Ace, 즉 (♠,A) 입니다.

이항연산을 함수로 표현

이항연산을 함수로 표현할려면 정의역(Domain)에 2개의 인자(argument)의 입력(Input)이 필요합니다. 그러면 이걸 어떡해야 할까요? 그걸 왜 지금 묻고있는걸까요?

답은 『곱집합(cartesian product, Product Set)』입니다.

$f((x,y)) = z$ 라고 가정을 한다면, $x\isin \mathbb R,y\isin \mathbb R$ 의 $\mathbb R \times \mathbb R \to \mathbb R$ 에서

튜플 $(x,y)$ 은 하나의 원소이기 때문에 함수의 입력으로 성립하고,

튜플 $(x,y)$ 은 각각 $x\isin \mathbb R,y\isin \mathbb R$ 의 원소를 갖고 있으므로

이항연산을 함수로 표현할 수 있습니다.

  
int Func((int,int) arg1)
{
	return arg1.item1 * arg1.item2; //wow!
}

…근데 이거 맞나요?

합성함수(Composite Function)

합성함수라 하면 말 그대로 함수들을 합성한 것입니다.

유희왕카드의 융합카드 사진을 넣고싶었는데, 융합과 합성은 다르니 넘어가겠습니다.

합성함수의 정의와 기호

함수들을 결합하여 새로운 함수를 얻는것을 합성함수라고 합니다.

또한 이 합성함수는 $g(f(x)) = (g \circ f)(x)$ 라고 표기합니다.

연산방법은 다음과 같이 진행됩니다.

$f$ 가 $x$ 를 입력받아 $f(x)$ 를 출력하고,
$g$ 는 이 $f(x)$ 를 입력받아 $g(f(x))$ 를 출력합니다.

이걸 한번에 뭉친걸 $(g \circ f)(x)$ , 합성함수라 하는겁니다.

그러면 뭐가 다르냐!? 연산을 한 번 덜해도 결과가 똑같습니다.

미리 계산해서 하나로 조립해둔 느낌입니다.

저희가 유도과정을 통해 공식을 찾아내고, 나중에는 공식만 써서 빠르게 계산하는것 처럼요.

비슷한 느낌으로는..

프로그래밍의 자료구조 - dictionary

혹은 메모이제이션 기법과 느낌은 비슷하다고 볼 수 있겠네요.

미리 계산해서 합쳐두면 나중에 쓸때 편하니까요.

아! 혹은 행렬이 있네요. 이게 맞는 것 같습니다.

항등함수와 역함수

항등함수(identity function) : 대응한 값이 같은값 입니다.

$f : A \to A$ , $f(x) = x$

역함수(inverse Function) : $y$ 가 $x$ 의 함수일 때 , 그 역으로 $x$ 를 $y$ 의 함수로 본 것 입니다.

$f^{-1}(x)$ 라고 합니다.

아까 그 설명하다 옆길로 샜을때, $f:\mathbb N→\mathbb Z$ 를 만드는 것 보았죠?

반대로 코드를 짜면 $f : \mathbb Z \to \mathbb N$ , 즉 역함수입니다.

근데 이 역함수는 막 만들 수 없습니다. 조건이 필요해요.

역함수를 가지기위한 함수의 조건

역함수 (inverse Function) 다시한번 : domain과 codomain을 역으로

전사(surjection)는 역함수를 보장하지 않음 (ex - domain.count > codomain.count 의 케이스)
단사(injection)는 역함수를 보장하지 않음 (ex - domain.count < codomain.count, codomain의 대응되지 않는 성분 존재 가능성)
전단사(Bijection)는 역함수를 보장

$\therefore$ 역함수를 가지기 위해선 전단사여야합니다

합성함수의 역함수 법칙

합성함수의 역함수란, 함수를 처리했던 것을 그대로 반대로 하면 됩니다.

즉 $f(x)$ 이후 $g(f(x))$ 가 된 값을 $r$ 이라 명할때, $g^{-1}(r)$ 이후 $f^{-1}(g^{-1}(r))$ 한 게 $x$ 가됩니다

물론 함수 $f(x), g(x)$ 모두 전단사 함수여야겠죠.

이를 정리하면 다음과 같습니다.

$(g \circ f)^{-1}(x) = f^{-1}(x) \circ g^{-1}(x) = f^{-1}(g^{-1}(x))$
$(g \circ f)^{-1} = f^{-1} \circ g^{-1}$

아참, 가역함수의 합성함수는 가역적이지만,

합성함수가 가역적이라고 각각의 함수가 가역적이지는 않습니다.

벡터

아까 곱집합에서 $\mathbb R^2$ , 직교좌표계(데카르트 좌표계, cartesian coordinate system)에 대해 잠시 언급한 적 있습니다.

이번에 다룰 내용은 직교좌표계을 주로 쓰게 될 것입니다.

왜냐하면 벡터란, 2 이상의 원소(요소)들에 의해 어떤 양을 표현하는데 유용한 표기법 이기 때문입니다. 스칼라의 다음 차원에 대응되는 개념이라고 보시면 됩니다.

앗 생각해보니 스칼라도 설명을 안드렸네요.

스칼라(Scalar)는 측도를 단위로 하여 크기만으로 결정되는 양입니다.

이렇게 된거 단어나 분류해 봅시다

집합과 원소를 주 관점으로 단어를 설명해 봅시다.

수 집합은 수를 원소로 하는 집합(Set)입니다.

수는 수 집합의 원소(Element)죠.

수 집합중 여러 조건을 만족하는 구조를 체(Field)라고 한다 했죠,

체(Field)라는 개념의 집합 속의 원소를 스칼라(Scalar) 라고 합니다.

거기서 나아가,

곱집합(Product Set,Cartesian Product) 은 두 집합 $S_1$ 의 원소 $x$ 와 $S_2$ 의 원소 $y$ 로 구성된 모든 순서쌍 $(x,y)$ 로 이루어진 집합입니다.

순서쌍(Ordered Pair ,Ordered Set)은 순서가 고려된 $n$ 개의 원소를 효과적으로 표현하는 방법입니다 튜플(tuple)로 표현할 수 있으며, 순서쌍 또한 하나의 집합입니다.

벡터 공간(Vector Space)은 n개의 체(Field)의 원소 $e_1$ , $e_2$ .. $e_n$ 로 구성된 원소들로 구성된 순서쌍(Ordered Pair) 속하는 집합이라고 생각합니다. 곱집합과 유사하게, 집합이 아닌 체를 대상으로 한다 봅니다.

벡터(Vector)는 2 이상의 원소들에 의한 양을 표현하는 방법이며, 벡터공간의 원소입니다.

아까 스칼라(Scalar)는 측도를 단위로 하여 크기만으로 결정되는 양이라고 하였습니다.

그에 비해 더 높은 차원을 갖는다고 볼 수 있죠.

하지만 수학에서는 꼭 방향과 크기를 나타내는 벡터로 제한시킬 필요는 없습니다.

좌표계(Coordinate System)은 공간 상에 좌표로 표현하기 위한 모든 좌표의 집합입니다.

아까 말했던 직교좌표계, 데카르트 좌표계(Cartesian Coordinate System)를 예시로 하자면, 각각의 축이 하나의 $\mathbb R$ 의 집합이며, 각각의 축이 직각을 이룹니다. 좌표축도 고정적인 좌표계이죠.

이에 속하는 위치정보는 좌표(Coordinates)이며, 위치의 수치를 나타냅니다.

예를들어 3차원 직교좌표계에서는 각 축의 요소를 $x,y,z$ 로 두고 ( $x,y,z)$ 로 표현합니다.

이렇게 집합과 원소의 관점에 대해 나눠보았습니다.

추가적으로 연산을 저 관점에서 한다면,

이항연산(binary operation)은 원소 두개로 다른 원소 하나 생성, 출력된 변수가 다시 그 집합의 원소가 됩니다.

어라 그런데 순서쌍은 집합이며 동시에 원소입니다.

이건 좀 있다가 다뤄봅시다.

벡터의 연산 및 공리, 벡터와 벡터공간

벡터의 연산에 대해 생각을 해봅시다.

일단 일반적으로 체에 포함된 연산을 개념적으로 본다면

덧셈은 축에 평행하게 위치를 이동시키는 것이고,
곱셈은 크기를 확대하거나 줄입니다.

벡터공간에서 단일 스칼라는 혼자 존재할 수 없습니다.

따라서 벡터와 스칼라의 덧셈은 불가능하겠죠.

생각하기에 (1,2) 에 1을 더하는건 불가능합니다.

다만 (1,2)에 x축으로 1을 더하는건 (1,0)이기 때문에 0이라는 2번째 순서(order)의 스칼라 값을 포함한 벡터가 되는겁니다.

즉 벡터의 덧셈은 벡터와 벡터의 덧셈입니다.

벡터와 벡터의 덧셈은, 각 순서(order)에 맞는 스칼라끼리 덧셈을 한 것과 같습니다.

따라서 $(a,b) + (c,d) = (a+c,b+d)$ 입니다.

하지만 곱셈은 생각을 해봐야합니다.

크기를 $n$ 배로 확장시키는 개념이라면, 크기만 있으면 됩니다.

즉 스칼라를 벡터와 연산시킬 수 있고, 이를 스칼라배(Scalar Multiplication)라고 합니다.

하지만 이 배율이라는건 어떤걸 기준으로 키우는 걸까요?

공간의 최저단위는 무엇일까요?

현실에서는 위로 1cm가 앞으로 1cm이며, 동시에 옆으로 1cm입니다.

모두 어떤 축을 기준으로 동일한 크기를 갖고 있죠.

어떠한 공간에서도 무조건 같을 수 있을까요?

그래서 단위를 찾다보니 기저(Basis)가 나왔습니다

기저는 가장 적은 수로써 선형독립을 이루며 벡터공간을 생성할 수 있는 것입니다.

또한 수학적 공간을 생성하는 최소의 집합이죠.

벡터공간 내에서 기저벡터(Basis Vector)의 집합은

선형독립(Linearly Independent)입니다 즉 하나의 벡터가 다른벡터들의 선형결합으로 다른 벡터를 정의할 수 없습니다. 하나의 벡터가 다른벡터의 선형결합에 의해 정의되는것은 선형의존(Linearly dependent)라고 합니다.
전체공간을 생성(Span)하게 됩니다

이에 따르는 기저벡터를 통해 배율을 정할 수 있게 되었습니다.

그 배율역시 사실 현실세계의 1:1:1 비율과 비교해서 보게되는 것이지, 해당공간에서는 같은 배율입니다.

다시 돌아와서, 스칼라배는 스칼라값을 모든 순서의 벡터내 스칼라에 곱하면 됩니다.

따라서 $(1,2)\space \alpha = (1 \space \alpha,2\space \alpha)$ 입니다

해당연산을 통해

벡터의 방향을 반대로 하거나(수직선에서 방향을 반대로 한 것과 같이)
벡터의 길이를 변화시킬 수 있습니다.

그저 적용되는게 수직선에서 벡터가 가르키는 방향으로 바뀔 뿐입니다.

자 이제 연산에 대해 생각을 해보았으니 공리를 보시죠.

벡터공간의 공리(Axiom)은 다음과 같습니다.

덧셈 연산( $+$ $+$ )에 대해
1. 닫혀 있음(closure)
2. 항등원(identity) 이 존재 ( zero vector ) $a + 0 = a = 0 + a$
3. 역원(inverse)이 존재 $a+(-a) = 0 = (-a) + a$
4. 결합법칙(associativity) 성립 $(a+b)+c = a+(b+c)$
5. 교환법칙(commutativity) 성립 $a+b=b+a$
스칼라배( Scalar Multiplication )에 대해 : 스칼라는 $\alpha \space \beta$ $α β$ 로 표현
1. 닫혀 있음(closure)
2. 항등원(identity) 이 존재 ( $1$ ) $a\space1 = a = 1\space a$
3. 결합법칙(associativity) 성립 $(\alpha\space \beta)\space a = \alpha\space(\beta\space a)$
4. 스칼라배와 벡터의 덧셈에 대한 분배법칙(distributivity) 성립 $\alpha \space (b+c) = \alpha\space b+\alpha\space c$
5. 스칼라의 덧셈과 벡터의 곱에 대한 분배법칙(distributivity) 성립 $(\alpha+\beta) a = \alpha\space a + \beta\space a$

공리를 통해 벡터를 다시 본다면

수학자들은 단지 벡터를 방향, 크기같은 것에 한정한 것이 아니라

벡터에 벡터를 더하는것과 벡터에 스칼라를 곱한다는 개념만 맞으면 된다는 것 같습니다.

하지만 물리학에서는 방향과 크기를 가지고 있죠

저희가 사용하는 컴퓨터공학에서는, 벡터는 단순한 순서를 지켜야하는 리스트이자 튜플입니다.

이걸 하나로 섞어봅시다.

2차원 평면에서 어떤 지점을 가르키는 화살표를 하나 생각합니다.

이 화살표의 시작지점은 원점이며, 가르키는 지점은 어떤 위치입니다.

이 위치를 정의하기 위한 정보를 갖게되는데, 2개의 순서쌍으로 이루어진 스칼라값들입니다.

이 2개의 순서쌍에 하나의 벡터가 대응하며, 하나의 벡터는 2개의 순서쌍의 표현을 가집니다.

아까 덧셈은 축에 평행한 이동이라고 적었습니다.

그리고 2차원 평면에서 축은 2개이며, 차원을 분리하여 각 축에 대한 스칼라값으로 분리할 수 있습니다. 그렇기 때문에 벡터의 덧셈은 연속된 이동을 하나의 이동으로 표현한 것이며, 새로운 벡터를 만듭니다. 예를 들어 (-2,3)+(3,4)의 경우는

x축 이동 : -2
y축 이동 : 3
x축 이동 : 3
y축 이동 : 4

를 순차적으로 행하였다고 볼 수 있습니다.

그리고 여기서는 평범하게 x축 이동, y축 이동 이라 적었고

그것의 단위또한 일정하지만, 이것역시 공간을 구성할 때 정의한다고 생각합니다.

만약 좌표계가 전체적으로 45도 돌아간, x : y = 1 : 1 비율을 가진 x’ 축과, x : y = -1 : 1 을 가진 y’축,

그 크기가 1이라고 가정하면 그 공간의 x’축과 y’축을 기준으로 한 이동역시 존재하겠죠.

어쨋거나 결국 벡터공간은 이런 가장 작은 단위의 벡터를 기반으로 구성된 공간입니다.

모든 벡터는 저 작은 단위의 벡터의 각 요소에 각각의 스칼라를 곱한 것으로 표현이 가능하게 되고

위치에 대한 개념을 갖지 않으므로 벡터공간에서는 크기와 방향만 갖다면 둘은 동일합니다.

저희가 프로그래밍을 진행하며 좌표에서 좌표를 뺀 벡터를 구하고, 좌표에서 벡터를 더해 좌표를 만드는 것은 벡터공간이 아닌 아핀공간(Affine Space)에서 다룹니다.

시각적으로 고정된 환경에서 보자면 원점에서 출발하여 어느지점을 가르키는 것이 벡터이며

시각적으로 고정적이지 않은 환경에서 보자면 벡터는 단지 어느방향으로 얼마만큼 이동하느냐 밖에 존재하지 않습니다.

좌표계에서 말하는 (1,2) 라는 위치는 벡터공간에서 존재할 수 없습니다.

다만 벡터공간에서는 ‘첫번째 순서(order)의 축으로 +1만큼, 두번째 순서(order)의 축으로 +2만큼’ 이라는 개념으로 존재하는것이죠.

즉 결국 벡터는 화살표입니다.

그리고 벡터공간은 원점, 0벡터(zero vector)로 부터 시작하는 무수히 많은 화살표가 있는 공간이죠.

벡터는 수인가 수가 아닌가

이 항목은 개인적인 생각을 정리해 보았습니다.

벡터는 수가 아니라고 생각합니다.

수는, 스칼라는 크기를 나타냅니다. 순수함의 결정체라고 생각합니다.

어떤 공간에 있어서 스칼라를 가지고 연산을 하였을때, 공간이 변하면 안된다고 생각합니다.

즉, 점에서는 점을 유지해야하고, 선에서는 선을 유지해야하며, 면에서는 면을 유지해야 한다고 생각합니다.

벡터는 화살표입니다.

어느 방향으로 얼마만큼 이라는 정보를 가진 화살표 입니다.

이 화살표에게 크기를 늘린다는것은, 진행하는 방향을 하나로 축으로 하는 직선에서의 크기입니다.

즉 벡터의 공간은 1차원 직선입니다.

단순화 한 예시를 생각해 봅시다.

(1,0)이라는 벡터가 있습니다. x축으로 1만큼, y축으로 0만큼 이동하는 간단한 직선입니다.

여기서 배율을 몇십,몇백, 무한대로 확장하더라도 y축으로는 0만큼 이동합니다.

즉, 이 벡터는 수직선과 동일하다고 보겠습니다.

그런데 이 벡터에게 방향이 담긴 정보가 들어갈 수 있을까요?

수직선의 좌표가 갑자기 위로 올라갈 수 있을까요?

각각의 벡터는 끝없이 확장하였을 때 하나의 선을 이룬다고 생각합니다.

그 벡터 내부의 세상은 다만 진행방향과 역방향 밖에 없습니다.

혹은 그 벡터가 0벡터라면 내부의 세상은 원점 뿐이겠죠.

이 상태에서 스칼라가 영향을 미쳐도 여전히 벡터 내부 세상의 규칙(차원)은 바뀌지 않습니다.

그러면 이제 벡터 공간에서 두개의 벡터를 선택한다고 가정합니다.

두개의 벡터에게 각각 스칼라배 한다고 생각해봅시다.

스칼라배는 아까 벡터 내부 세상의 규칙을 바뀌지 않는다 하였습니다.

아마 대다수의 벡터를 통해 만들어진 무수히 많은 점을 모두 연결한다면

면이 나오게 될 것입니다. 즉 한 벡터가 다른 벡터에게 영향을 미친 결과가 벡터 하나의 세상을 벗어나게 됩니다.

(물론 둘이 가르키는 방향이 동일하다면 동일한 세상이겠지만, 아닌 케이스가 더 중요하니 넘어가겠습니다.)

따라서 벡터(Vector)는 수(Number) 일 수 없다고 생각합니다.

글을 쓰며

벡터에 대한걸 원래 사용하던 방식이 아니라 모든걸 리셋하고 생각을 하는게 어려웠습니다.

제가 알고있는 것이

아무래도 정답만을 위해 달려오던 교육환경때문인지,

스스로 생각하는 논리를 펼치는게 거부감이 들었습니다.

이런 생각을 하다가 잠들었더니 꿈에서 혼났습니다.

그리고 오히려 그런것 때문에 발전을 못하는게 아닌가? 라는 생각이 들었습니다.

그래서 이번글은 최대한 개인적인 생각으로 이해를 해봤습니다.

따라서 논리적으로 맞지 않거나, 명료하지 않거나, 추상적이거나, 정답이 아닐 수 있습니다.

부족한 글 읽어주셔서 감사합니다.

2. Function & Vector