Quaternion interpolation & Skinning
머릿말
정신이 정말 하나도 없네요
사원수 보간
사원수의 선형 보간과 구면 선형 보간(Lerp & Slerp)
저희가 일반적으로 사용해온 선형보간은, 두 점에 대한 변위 비율로 곱하여 더했었습니다.
대충 다음과 같은 방법이라고 보면 되는 것이죠
1
2
3
4
5
6
7
8
9
10
11
Quaternion LERP(const Quaternion& a, const Quaternion& b, const float t)
{
Quaternion r;
float t_ = 1 - t;
r.x = t_*a.x + t*b.x;
r.y = t_*a.y + t*b.y;
r.z = t_*a.z + t*b.z;
r.w = t_*a.w + t*b.w;
r.Normalize();
return r;
}
하지만 이렇게 처리한다면 사실 회전에 대해서는 정확하지 않습니다.
마치 원근투영보정 처럼요.
그러면 회전은 각이니 각 단위로 보간을 해줘야겠죠?
그것을 Slerp, Spherical lerp라고 말합니다.
각으로 나누고, 크기가 동일하다면 구를 띄게되니 구면-이라는 단어가 붙는 것이죠.
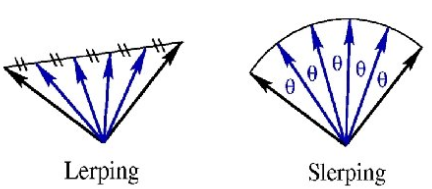
사원수의 구면 선형 보간 방법
그러면 일단 보간식부터 다시 들어가볼까요?
회전에 대해 나타내야하므로, t와 1-t가 아닌 두 임의의 값 , 로 표현하면 다음과 같습니다.
그리고 이를 벡터로 시각화한다면,
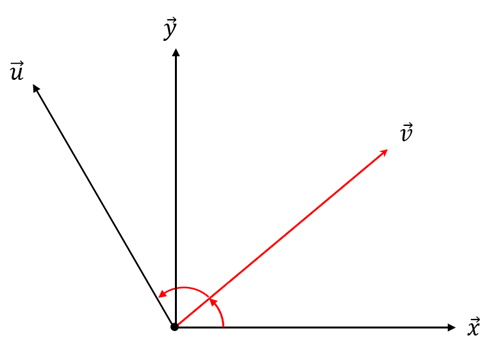
다음과 같은 형태를 띄게 됩니다.
알고있는 정보는 벡터 x와 벡터 u.
그러면 벡터v와 직교하는 벡터y를 구해야합니다.
벡터 v는 간단하게 정의할 수 있습니다.
그러면 직교벡터를 구해야겠죠.
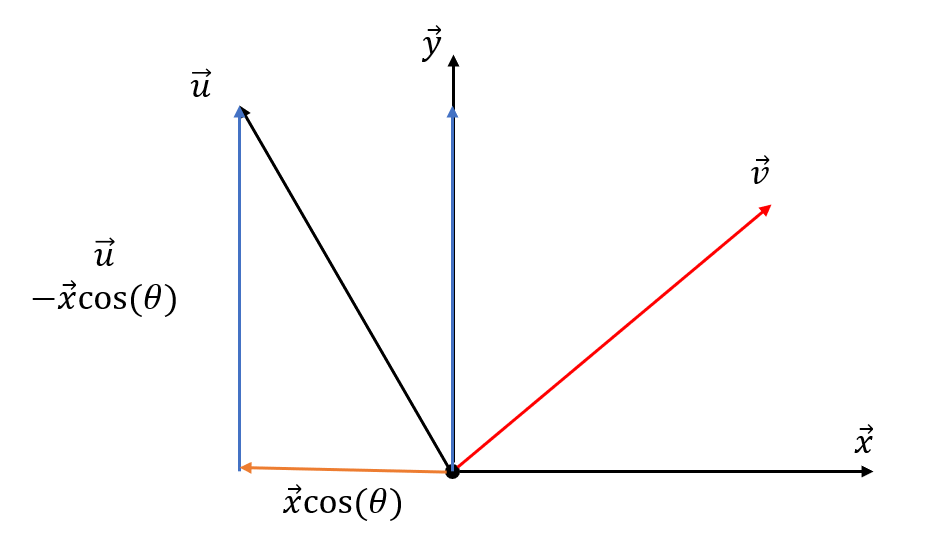
직교벡터는 간단하게 벡터u에서 x로 이동한 만큼 빼주면 됩니다.
정리하면
그러므로,
단, 여기서 분모가 0이 되면 안되기때문에 처리를 해줘야합니다.
sin함수는 너무 무거우니, 간단하게 내적을 통해 내적의 절댓값이 1에 충분히 가깝다면
(이는 코사인 90에 가깝다면이고, 사인 0에 가깝다면 으로 읽을 수 있습니다)
일반적인 선형보간으로 처리합니다.
짧은 경로로 구면 보간을 수행하기 위한 방법을 정리하고 구현된 언리얼 엔진의 코드를 분석하시오.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
FQuat FQuat::Slerp_NotNormalized(const FQuat& Quat1,const FQuat& Quat2, float Slerp)
{
// 분모가 0에 가까워지는 경우를 판단하기 위한 sin값 대신 사용할 cos값,
// 즉 내적값을 구합니다
const float RawCosom =
Quat1.X * Quat2.X +
Quat1.Y * Quat2.Y +
Quat1.Z * Quat2.Z +
Quat1.W * Quat2.W;
//절댓값 처리를 진행합니다.
//FMath::FloatSelect는 부동소숫점정밀도를 위한 특수한? 삼항연산자로 보입니다.
const float Cosom = FMath::FloatSelect( RawCosom, RawCosom, -RawCosom );
float Scale0, Scale1;
// 내적 값이 1에 너무 가까워지면 (==sin값이 0에 가까워지면)
// 부동소숫점 오류특성상 문제를 야기할 수 있으므로, 판별을 진행합니다.
if( Cosom < 0.9999f )
{
// 구면선형보간 영역
// 위에서 구한 대로 계산합니다.
const float Omega = FMath::Acos(Cosom);
const float InvSin = 1.f/FMath::Sin(Omega);
Scale0 = FMath::Sin( (1.f - Slerp) * Omega ) * InvSin;
Scale1 = FMath::Sin( Slerp * Omega ) * InvSin;
}
else
{
// 선형보간영역
// 어짜피 구면선형보간을 처리한다면 더 큰 오차가 나기때문에
// 이때는 선형보간이 더 적은 오차를 갖게 됩니다.
// 또한 애초에 너무 작은 범위에서만 처리하기 때문에 구의 표면적을 계산하듯,
// 그냥 직선이라고 생각해도 무방합니다.
Scale0 = 1.0f - Slerp;
Scale1 = Slerp;
}
// 내적을 통해 정면과 뒷면을 알 수 있습니다.
// 더 짧은 경로로 가야하므로 내적 결과가 양수인 값인
// (즉, 비교 대상 벡터가 양 방향으로 존재할 때 그나마 유사한,각도가 90보다 작은)
// 벡터를 사용하면 됩니다.
Scale1 = FMath::FloatSelect( RawCosom, Scale1, -Scale1 );
FQuat Result;
Result.X = Scale0 * Quat1.X + Scale1 * Quat2.X;
Result.Y = Scale0 * Quat1.Y + Scale1 * Quat2.Y;
Result.Z = Scale0 * Quat1.Z + Scale1 * Quat2.Z;
Result.W = Scale0 * Quat1.W + Scale1 * Quat2.W;
return Result;
}
강제로 긴 경로로 구면 보간을 수행하는 코드를 구현하고, 이를 실행한 결과를 움짤로 첨부하시오.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
FQuat FQuat::Slerp_NotNormalized(const FQuat& Quat1,const FQuat& Quat2, float Slerp)
{
const float RawCosom =
Quat1.X * Quat2.X +
Quat1.Y * Quat2.Y +
Quat1.Z * Quat2.Z +
Quat1.W * Quat2.W;
const float Cosom = FMath::FloatSelect( RawCosom, RawCosom, -RawCosom );
float Scale0, Scale1;
if( Cosom < 0.9999f )
{
//등각성을 유지 해야하므로, 여기서도 각도를 뒤집어줘야합니다.
const float Omega = FMath::Acos(-Cosom);
const float InvSin = 1.f/FMath::Sin(Omega);
Scale0 = FMath::Sin( (1.f - Slerp) * Omega ) * InvSin;
Scale1 = FMath::Sin( Slerp * Omega ) * InvSin;
}
else
{
Scale0 = 1.0f - Slerp;
Scale1 = Slerp;
}
//내적값을 뒤집든, 결과를 뒤집든 뒤집는다면,
//양방향 두 벡터중 유사도가 더 낮은 벡터를 대상으로 처리되므로(즉 각이 90보다 큰 방향),
//긴 경로 보간을 진행하게 됩니다.
Scale1 = FMath::FloatSelect( RawCosom, -Scale1, Scale1 );
FQuat Result;
Result.X = Scale0 * Quat1.X + Scale1 * Quat2.X;
Result.Y = Scale0 * Quat1.Y + Scale1 * Quat2.Y;
Result.Z = Scale0 * Quat1.Z + Scale1 * Quat2.Z;
Result.W = Scale0 * Quat1.W + Scale1 * Quat2.W;
return Result;
}
하지만 어림도없죠. 테스트대상은 유니티입니다.
테스트코드를 작성해볼까요?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
public class QuaternionTester : MonoBehaviour
{
[SerializeField]
private GameObject Point;
private List<GameObject> trash = new List<GameObject>();
[SerializeField]
private bool useInverse;
private void OnEnable()
{
if (Point == null)
return;
StartCoroutine(Run());
}
IEnumerator Run(float runtime = 1f)
{
float t = 0;
Quaternion defaultRot = transform.rotation;
Quaternion target = Quaternion.LookRotation(new Vector3(-1, 0, -1));
while (t < runtime)
{
var instance = Instantiate(Point, null);
instance.transform.position = Point.transform.position;
instance.transform.rotation = Point.transform.rotation;
trash.Add(instance);
transform.rotation = Slerp(defaultRot, target, t / runtime);
t += Time.deltaTime;
yield return null;
}
}
private void OnDisable()
{
foreach(var instance in trash)
{
Destroy(instance);
}
trash.Clear();
}
Quaternion Slerp(in Quaternion Quat1, in Quaternion Quat2, float Slerp)
{
float RawCosom =
Quat1.x * Quat2.x +
Quat1.y * Quat2.y +
Quat1.z * Quat2.z +
Quat1.w * Quat2.w;
float Cosom = RawCosom > 0 ? RawCosom : -RawCosom;
float Scale0, Scale1;
if (Cosom < 0.9999f)
{
float Omega = Mathf.Acos(useInverse ? -Cosom : Cosom);
float InvSin = 1f / Mathf.Sin(Omega);
Scale0 = Mathf.Sin((1f - Slerp) * Omega) * InvSin;
Scale1 = Mathf.Sin(Slerp * Omega) * InvSin;
}
else
{
Scale0 = 1.0f - Slerp;
Scale1 = Slerp;
}
Scale1 = RawCosom > 0 ? Scale1 : -Scale1;
if (useInverse)
Scale1 *= -1;
Quaternion Result = Quaternion.identity;
Result.x = Scale0 * Quat1.x + Scale1 * Quat2.x;
Result.y = Scale0 * Quat1.y + Scale1 * Quat2.y;
Result.z = Scale0 * Quat1.z + Scale1 * Quat2.z;
Result.w = Scale0 * Quat1.w + Scale1 * Quat2.w;
return Result;
}
}
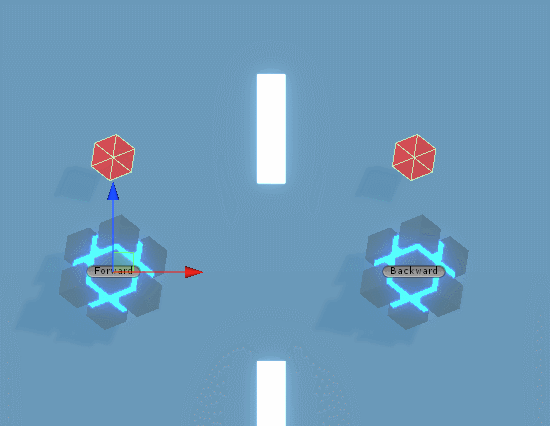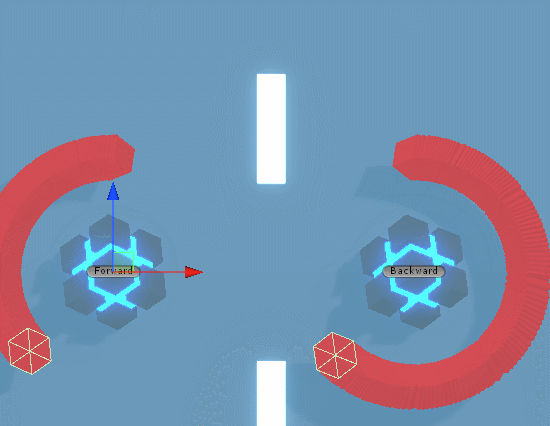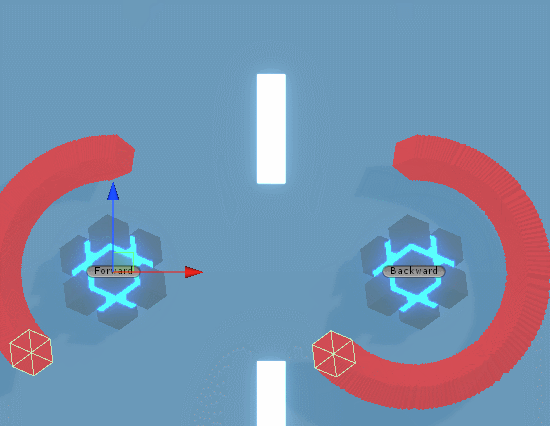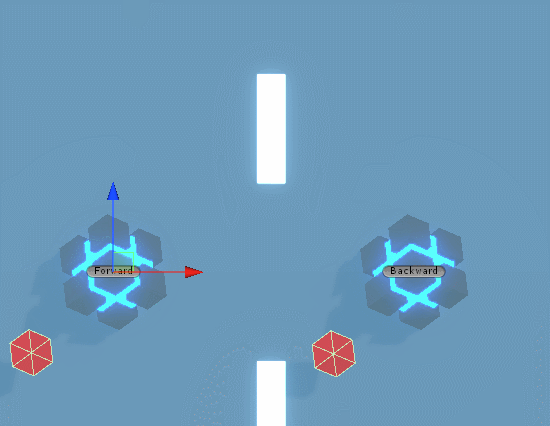
짜잔 입니다.
트리비아
사실 이것은 처음엔 문제가 있었습니다.
초기 함수 코드입니다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Quaternion Slerp(in Quaternion Quat1, in Quaternion Quat2, float Slerp)
{
float RawCosom =
Quat1.x * Quat2.x +
Quat1.y * Quat2.y +
Quat1.z * Quat2.z +
Quat1.w * Quat2.w;
float Cosom = RawCosom > 0 ? RawCosom : -RawCosom;
float Scale0, Scale1;
if (Cosom < 0.9999f)
{
float Omega = Mathf.Acos(Cosom); // <<이쪽은 부호를 바꾸지 않습니다
float InvSin = 1f / Mathf.Sin(Omega);
Scale0 = Mathf.Sin((1f - Slerp) * Omega) * InvSin;
Scale1 = Mathf.Sin(Slerp * Omega) * InvSin;
}
else
{
Scale0 = 1.0f - Slerp;
Scale1 = Slerp;
}
Scale1 = RawCosom > 0 ? Scale1 : -Scale1;
if (useInverse)
Scale1 *= -1;
Quaternion Result = Quaternion.identity;
Result.x = Scale0 * Quat1.x + Scale1 * Quat2.x;
Result.y = Scale0 * Quat1.y + Scale1 * Quat2.y;
Result.z = Scale0 * Quat1.z + Scale1 * Quat2.z;
Result.w = Scale0 * Quat1.w + Scale1 * Quat2.w;
return Result;
}
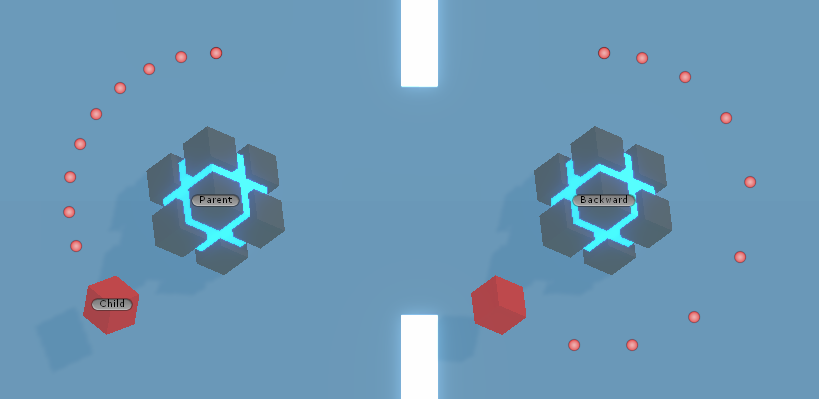
보이시나요? 역방향회전일때 등각이 아닙니다.
더 다이나믹 하게 바꿔보았습니다.
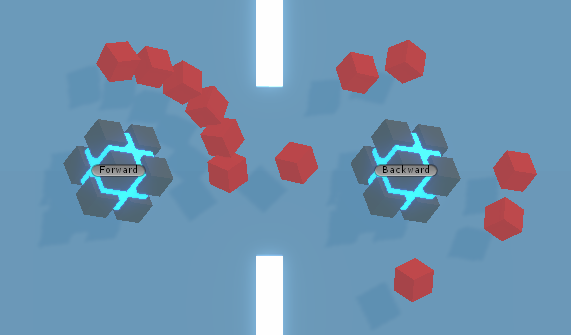
이제 확실히 역회전은 등각이 아니라는 것을 볼 수 있습니다
왜 그렇게 되는가?
“음? 걍 어쨋든 곱만 바꿔주면 되는거 아님?” 했던게 문제입니다.
왜냐하면 회전각 보간 자체는 정방향으로 계산하고 팩터만 반대로 곱했기 때문이죠.
조금 수정해줍니다
1
2
3
4
5
6
7
8
9
10
11
12
float Cosom = RawCosom > 0 ? RawCosom : -RawCosom;
if (Cosom < 0.9999f)
{
//float Omega = Mathf.Acos(Cosom);
//각을 받아오는것은 결국 여기인데, 여전히 예각을 받아오고 있었음.
float Omega = Mathf.Acos(-Cosom); //따라서 둔각을 받아오도록 수정
float InvSin = 1f / Mathf.Sin(Omega);
Scale0 = Mathf.Sin((1f - Slerp) * Omega) * InvSin;
Scale1 = Mathf.Sin(Slerp * Omega) * InvSin;
}
if문 밖에서 수정하게되면, 음수에 의해 선형보간으로 넘어가게 됩니다.
따라서 내부각을 가져오는 아크코사인 함수에서 음수를 넘겨 반대 각을 가져오는겁니다.
그러면 짜잔
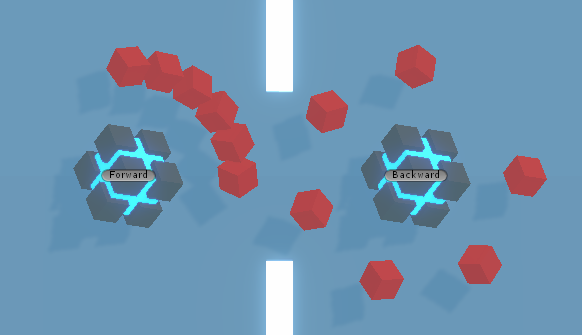
역방향에서도 등각이 잘 유지됩니다.
일반화 한다면?
만약 일반화 한다면 다음과 같을 것 같습니다.
일단, divide 0 를 피하기 위한 검사에서, 절댓값을 씌워서 검사하고,
cosom(코사인 오메가)의 부호는 예각회전인지 둔각회전인지에 따라 선택할 수 있도록 둡니다.
그리고 rawCosom의 부호판별을 모두 감싸서, 어느회전인지에 따라 부호를 다시 결정하게 합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void Func()
{
var rotatePred = new Predicate<float>((rawCos) => rawCos > 0); //예각회전
var invRotatePred = new Predicate<float>((rawCos) => rawCos < 0);//둔각회전
var pred = useInverse ? invRotatePred : rotatePred; //예각인지 둔각인지 결정
var rotate = Slerp(a.rotation,b.rotation,t,pred);
}
Quaternion Slerp(in Quaternion Quat1, in Quaternion Quat2,
float Slerp, Predicate<float> pred)
{
float RawCosom =
Quat1.x * Quat2.x +
Quat1.y * Quat2.y +
Quat1.z * Quat2.z +
Quat1.w * Quat2.w;
float Cosom = pred(RawCosom) ? RawCosom : -RawCosom; //modified -pred
float Scale0, Scale1;
if (Mathf.Abs(Cosom) < 0.9999f) //modified -abs
{
float Omega = Mathf.Acos(Cosom);
float InvSin = 1f / Mathf.Sin(Omega);
Scale0 = Mathf.Sin((1f - Slerp) * Omega) * InvSin;
Scale1 = Mathf.Sin(Slerp * Omega) * InvSin;
}
else
{
Scale0 = 1.0f - Slerp;
Scale1 = Slerp;
}
Scale1 = pred(RawCosom) ? Scale1 : -Scale1; //modified -pred
Quaternion Result = Quaternion.identity;
Result.x = Scale0 * Quat1.x + Scale1 * Quat2.x;
Result.y = Scale0 * Quat1.y + Scale1 * Quat2.y;
Result.z = Scale0 * Quat1.z + Scale1 * Quat2.z;
Result.w = Scale0 * Quat1.w + Scale1 * Quat2.w;
return Result;
}
캐릭터 애니메이션

안녕하세요, 리깅입니다. (Hello, Rig) (2트)
스키닝 애니메이션
만약 메쉬를 수정할 때 모든 버텍스를 직접 조작하면 좋겠지만,
오래걸리고 번거로우니 트랜스폼의 부모 개념인 본(Bone) 기준으로 이동하도록 설정하는 것입니다.
하지만 그렇게 되면 관절부분이 이동하거나 회전할때 찢어지게 되겠죠?
그걸 해결하기 위해 스키닝을 사용하게 됩니다.
버텍스마다 어떤 본들의 이동에 더 초점을 두는지를 계산하게 되는데요,
무게중심좌표를 임의로 설정하여 어느쪽 본에 더 가까운지(영향을 받는지)를 나타낸다고 생각하면 편합니다.
그렇게 구현된 skinned Mesh는 약간 고무풍선과 유사하다고 생각하시면 됩니다.
늘리면 늘어나고, 돌리면 꺾입니다. 모두 이어진 상태로요.
이때 설정하는 무게중심좌표를 Weight, 가중치라고 부릅니다.
자기자신의 과제를 복붙하는 사람이 여기 한명 있습니다.
스키닝 애니메이션을 위해 필요한 메시 정보에 대해 정리하시오.
얜 2D랑 같습니다.
일단 위에서 기술하였듯, 본이라는 개념이 필요합니다.
본(Bone)은 일단 위치정보를 들고 있어야 하므로 트랜스폼을 가지고있어야하며,
본과 본을 구분할 수 있는 구분자가 필요합니다. 이때 키로 이름을 사용하게 됩니다.
또한 어디에 있었는지 최초의 값이 필요합니다. 이를 BindPose라 합니다.
버텍스관점에서 생각해봅시다.
버텍스는 어떤본의 이동에 대해 얼마만큼 이동을 할지 결정해야합니다.
즉 1개의 본에 대해서는 해당 본을 알고있어야하며, 얼마나 영향을 받는지를,
2개의 본에 대해서는 각 본을 알고 있어야하며,
각 본에 대한 영향치(결국 1이 되어야 하는 아핀조합을 생각하면 편할 것 같습니다. )
를 가지고 있어야 할 것 입니다.
따라서 각 버텍스는 추가적으로
연결된 본의 이름(구분자)와 해당 본에 대응하는 weight값을 가진 ‘리스트’가 필요합니다.
정리하자면
- Bone (뼈)
- 트랜스폼(Transform) - 이동 회전 스케일을 위해 필요합니다.
- 식별자(대게 이름) - Bone 을 구분하기 위해 필요합니다.
- BinePose - 본의 최초 트랜스폼 설정값입니다.
- Vertex
- 가중치의 갯수
- 연결된 Bone 의 리스트(List
) - 연결된 Bone 에 대한 가중치 리스트
계층 구조를 만들기 위해 고려해야 할 경우를 몇 가지 정리하고 각 경우마다 부모, 자신, 자식과의 월드/로컬 트랜스폼이 어떻게 변화되는지 정리하시오.
월드트랜스폼이 변경되는 경우
- 부모의 월드 트랜스폼이 변경되는 경우
- 이 경우 자기자신의 로컬 트랜스폼은 변화하지 않습니다
- 자기자신 및 자식의 월드 트랜스폼은 변화합니다.
- 자기 자신의 로컬트랜스폼이 변경될 경우
- 로컬좌표가 수정되었으므로, 월드좌표도 수정되어야겠죠.
로컬트랜스폼이 변경되는 경우
- 자기자신의 월드/로컬 트랜스폼이 변할 경우
- 부모가 변경되는 경우
- 월드트랜스폼은 변화하지 않지만 로컬트랜스폼은 새로운 부모에 대해 다시 비교하여 산출합니다.
정리하면 ‘어떤 물체의 월드 및 로컬 좌표계값’이 바뀌면 ‘하위객체의 모든 월드트랜스폼’이 바뀌며,
부모가 변경되는 경우에만 변경된 부모를 가지는 하나의 객체의 로컬트랜스폼만 재산출합니다.
유니티와 언리얼이 가진 계층 구조 구현의 차이를 분석하시오.
(크기 변환을 고려해 회전하는가? 크기 변환을 고려하지 않고 회전하는가? )
유니티의 스케일링된 부모 하위의 자식 회전

언리얼에서의 스케일링된 부모 하위 자식 회전
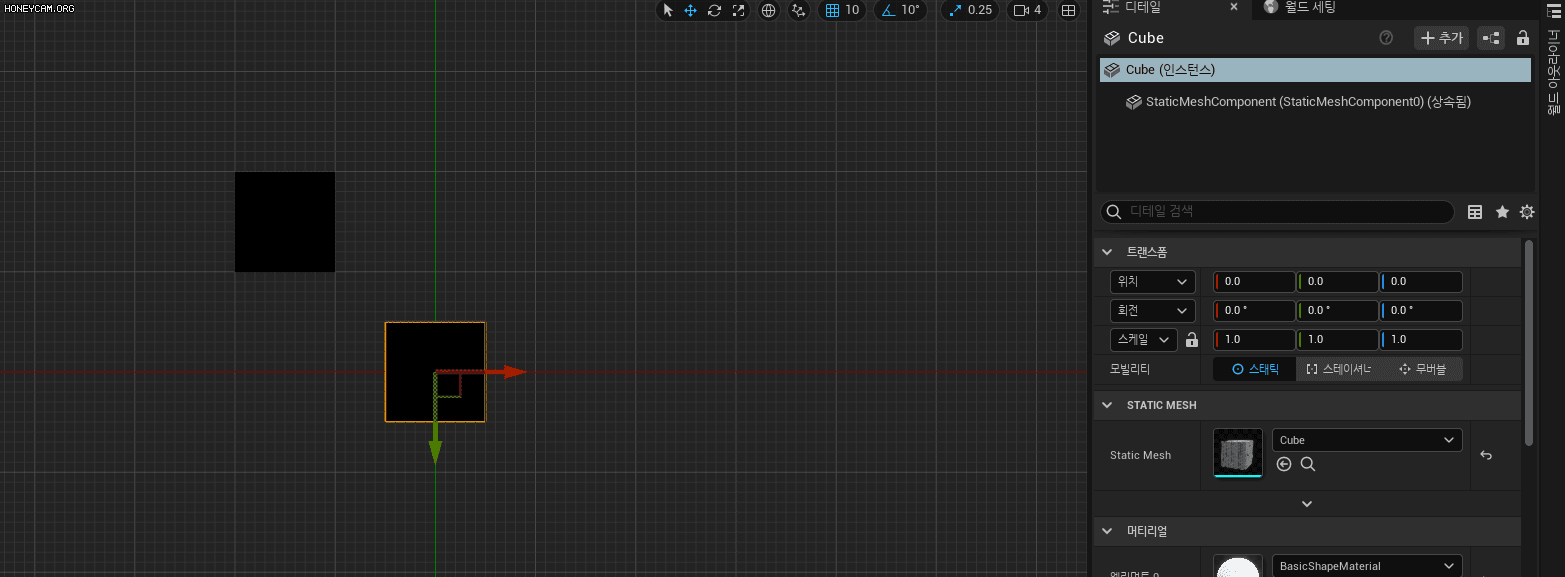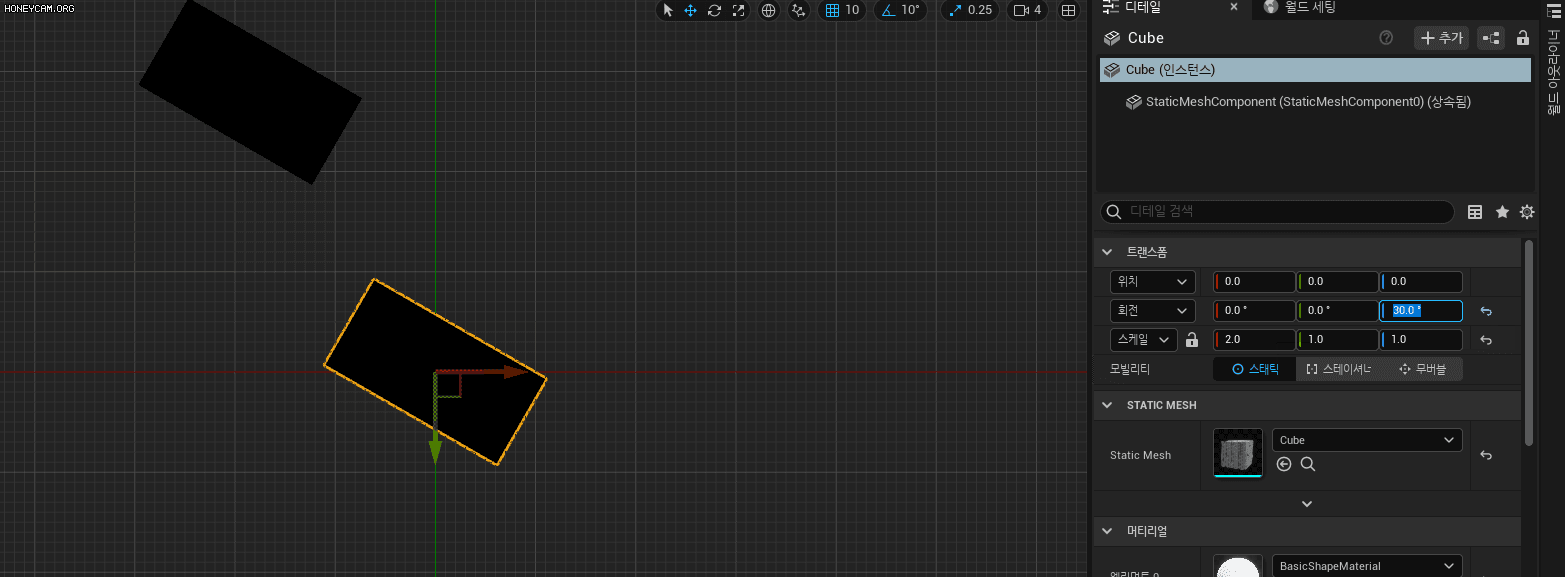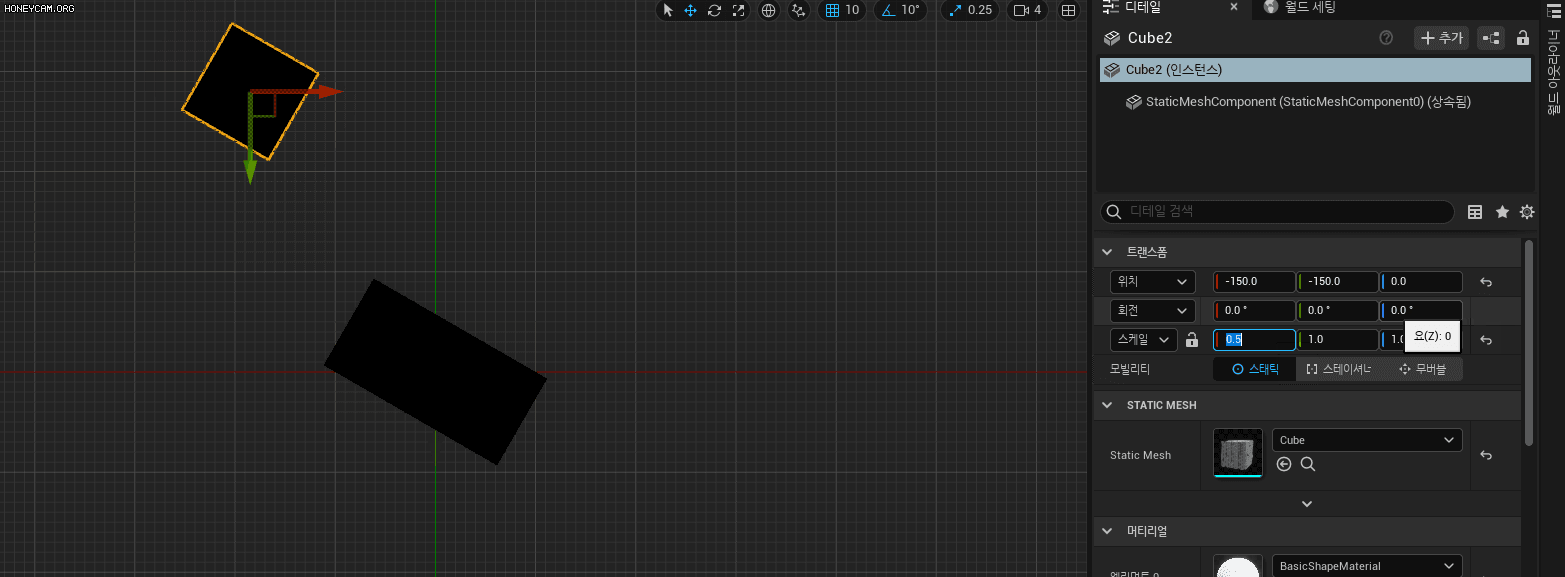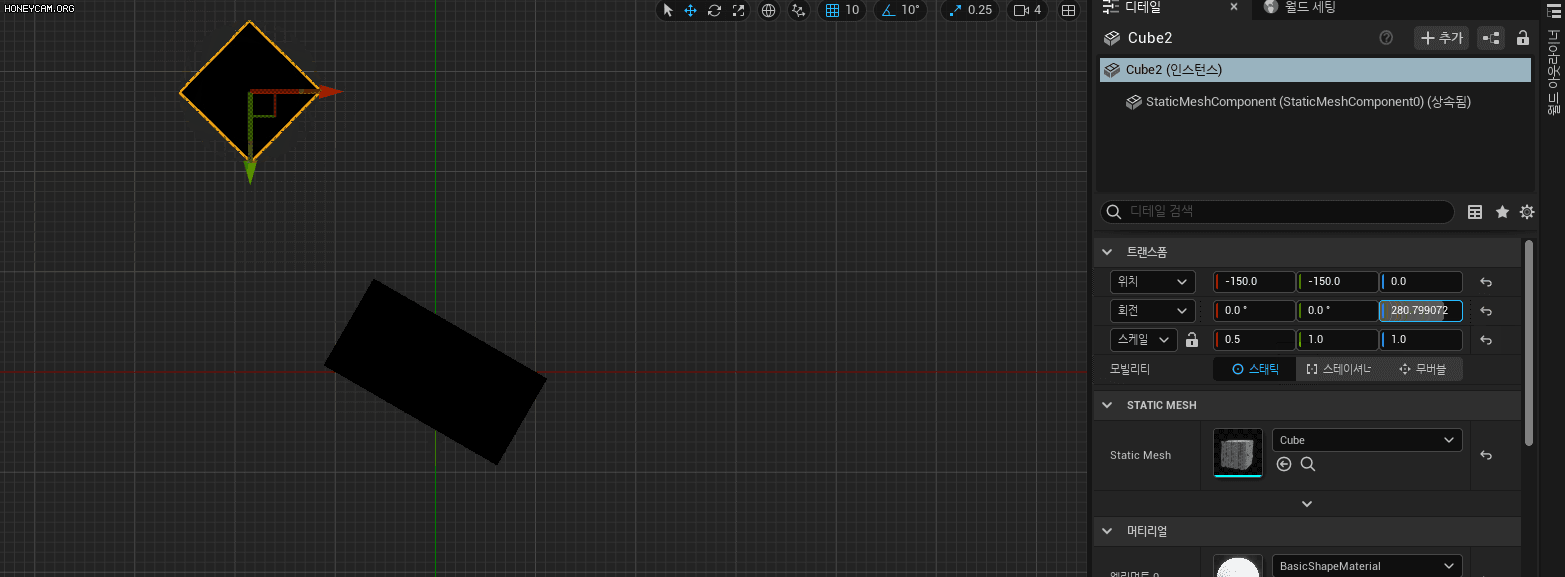
크기 변환과 회전 변환을 서로 분리하는 경우 LocalToWorld와 WorldToLocal을 구성하는 수식을 유도하고 이를 코드로 나타내시오.
LocalToWorld
1
2
3
4
5
6
7
8
9
FORCEINLINE constexpr Transform Transform::LocalToWorld(const Transform& InParentWorldTransform) const
{
// 현재 트랜스폼 정보가 로컬인 경우
Transform result;
result.Rotation = InParentWorldTransform.Rotation * Rotation;
result.Scale = InParentWorldTransform.Scale * Scale;
result.Position = InParentWorldTransform.Position + InParentWorldTransform.Rotation.RotateVector(InParentWorldTransform.Scale * Position);
return result;
}
WorldToLocal
1
2
3
4
5
6
7
8
9
10
11
12
FORCEINLINE constexpr Transform Transform::WorldToLocal(const Transform& InParentWorldTransform) const
{
// 현재 트랜스폼 정보가 월드인 경우
Transform invParent = InParentWorldTransform.Inverse();
Transform result;
result.Scale = invParent.GetScale() * Scale;
result.Rotation = invParent.GetRotation() * Rotation;
result.Position = invParent.Position + invParent.Rotation.RotateVector(invParent.Scale * Position);
//result.Position = invParent.Position + (invParent.Rotation * Position) * invParent.Scale;
return result;
}
캐릭터가 가져야 할 기본적인 본 구조에 대해 정리하시오.
아.. 이거 IK잡는다고 징그럽게 했었죠…
어떤 캐릭터에 따라 다르겠지만, 이족보행을 하는 형상에 대해 Biped라고 말합니다.
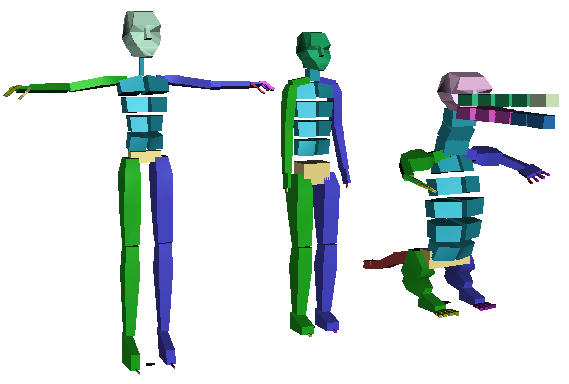
그리고 Max등에서 Biped의 계층구조를 일반적인 구조로 두며,

대략 위와 같은 구조를 따릅니다.
캐릭터에 따라, 게임에 따라, 사용처에 따라 수정될 수 있으며,
만약 양갈래머리캐릭터다, 혹은 손가락도 무언가 들어간다 한다면


이런식으로도 본이 들어갈 수 있겠죠.
기본이란 Pevis, Com, 아무튼 제일 중심이 되는 그 하나만 존재하면 됩니다.
위의 내용은 ‘이족보행 동물’의 ‘일반적인’ 본 구조라고 보는게 맞겠죠.
맺으며
이렇게 3D 스키닝 애니메이션의 구조까지 진행이 되었습니다.
12시간 VR프로젝트도 그렇고 팀플도 그렇고 요즘 갑자기 밤샘을 하니까
컨디션이 안좋아지는게 느껴집니다.
