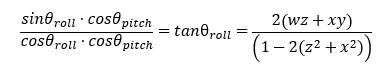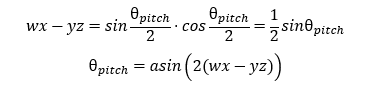Quaternion
머릿말 최근 일이 있어서 자꾸 부산과 이천을 왔다갔다한다고 너무 힘듭니다..
길가에서 핸드폰으로 수강하는데, 솔직히 이번주차는 해보고 싶었지만 환경이 안따라주어서 교수님과 수업을 같이 못해 아쉽습니다.
다음주에는 단체로 참석해보고 싶네요.
사원수의 회전 사원수의 회전을 설명하기에 좋은 시각화 자료가 있어 추가적으로 첨부합니다.
https://eater.net/quaternions
자연지수함수를 활용해 실수부가 0인 3차원 공간에서의 회전을 보장하는 사원수 곱셈 qvq*을 유도하시오. 저번주차에서 이어지는 내용입니다.
11주차
3차원공간의 벡터를 순허수 사원수로 표현하여 회전, 즉 곱셈 연산을 시켰다면,
다음과 같은 꼴로 볼 수 있습니다.
( c o s θ , u ⋅ s i n θ ) ⋅ ( 0 , v ⃗ ) (cos\theta,u\cdot sin\theta) \cdot (0,\vec{v}) ( cos θ , u ⋅ s in θ ) ⋅ ( 0 , v ) 이걸 계산하게 되면 실수부에 값이 생기게 되는데,
실수부에 값이 생겼다는 것은 3차원 공간에 표현할 수 없다 가 되므로 …. 무언가 다른 방법이 필요하겠죠.
그러면 실수부가 0인 공간에서 회전을 보장할 순 없을까요?
의외로 단순할지도 모릅니다.
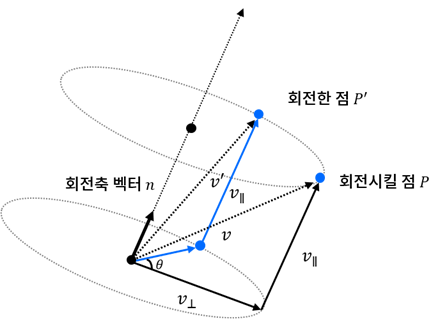
회전방식 일단 사원수의 회전을 생각할 때에는 이제 예전에 하였던 로드리게스 회전 방식을 사용하면 됩니다.(그래서 로드리게스를 한 것이죠)
그 중 정확이 어떤 부분인가,
바로 벡터를 수직과 수평으로 분리하여 생각하자는 것입니다.
그러면 로드리게스때와 마찬가지로
회전축벡터와 수직인 성분만 회전각만큼 회전하는 것입니다.
귀찮은 회전은 처리했으니, 평행인부분은 그냥 더해주면 되는 것이죠.
분리하면 뚝-딱입니다
지수함수로 표현 l e t , e n ^ θ = ( c o s θ , u ^ ⋅ s i n θ ) e n ^ θ ⋅ v ⃗ = ( − ( u ^ ⋅ v ⃗ ) s i n θ , c o s θ v ⃗ + ( u ^ × v ⃗ ) s i n θ ) let, \quad e^{\hat{n}\theta}=(cos\theta, \hat{u}\cdot sin\theta)\\ e^{\hat{n}\theta}\cdot\vec{v}=(-(\hat{u}\cdot\vec{v})sin\theta,cos\theta\vec{v}+(\hat{u}\times\vec{v})sin\theta) l e t , e n ^ θ = ( cos θ , u ^ ⋅ s in θ ) e n ^ θ ⋅ v = ( − ( u ^ ⋅ v ) s in θ , cos θ v + ( u ^ × v ) s in θ ) 분리한 벡터의 직교성분과 회전 e n ^ θ ⋅ v ⊥ ⃗ = ( 0 , c o s θ v ⊥ ⃗ + ( u ^ × v ⊥ ⃗ ) s i n θ ) e^{\hat{n}\theta}\cdot\vec{v_{\perp}}=(0,cos\theta\vec{v_{\perp}}+(\hat{u}\times\vec{v_{\perp}})sin\theta) e n ^ θ ⋅ v ⊥ = ( 0 , cos θ v ⊥ + ( u ^ × v ⊥ ) s in θ ) 외적의 반수성질을 사용하여 교환 정리
이거 나중에 써먹을꺼니까 미리 정리해둡시다.
v ⊥ ⃗ ⋅ e n ^ θ = ( 0 , c o s θ v ⊥ ⃗ + ( v ⊥ ⃗ × u ^ ) s i n θ ) = ( 0 , c o s θ v ⊥ ⃗ − ( u ^ × v ⊥ ⃗ ) s i n θ ) v ⊥ ⃗ ⋅ e n ^ ( − θ ) = ( 0 , c o s ( − θ ) v ⊥ ⃗ − ( u ^ × v ⊥ ⃗ ) s i n ( − θ ) ) = ( 0 , c o s θ v ⊥ ⃗ + ( u ^ × v ⊥ ⃗ ) s i n θ ) ∴ e n ^ θ ⋅ v ⊥ ⃗ = v ⊥ ⃗ ⋅ e n ^ ( − θ ) \vec{v_{\perp}}\cdot e^{\hat{n}\theta}=(0,cos\theta\vec{v_{\perp}}+(\vec{v_{\perp}}\times\hat{u})sin\theta)\\=(0,cos\theta\vec{v_{\perp}}-(\hat{u}\times\vec{v_{\perp}})sin\theta)\\\vec{v_{\perp}}\cdot e^{\hat{n}(-\theta)}=(0,cos(-\theta)\vec{v_{\perp}}-(\hat{u}\times\vec{v_{\perp}})sin(-\theta))\\=(0,cos\theta\vec{v_{\perp}}+(\hat{u}\times\vec{v_{\perp}})sin\theta)\\ \space\\ \therefore e^{\hat{n}\theta}\cdot\vec{v_{\perp}}=\vec{v_{\perp}}\cdot e^{\hat{n}(-\theta)} v ⊥ ⋅ e n ^ θ = ( 0 , cos θ v ⊥ + ( v ⊥ × u ^ ) s in θ ) = ( 0 , cos θ v ⊥ − ( u ^ × v ⊥ ) s in θ ) v ⊥ ⋅ e n ^ ( − θ ) = ( 0 , cos ( − θ ) v ⊥ − ( u ^ × v ⊥ ) s in ( − θ )) = ( 0 , cos θ v ⊥ + ( u ^ × v ⊥ ) s in θ ) ∴ e n ^ θ ⋅ v ⊥ = v ⊥ ⋅ e n ^ ( − θ ) 분리한 벡터의 평행성분과 회전 e n ^ θ ⋅ v ∥ ⃗ = ( − ( u ^ ⋅ v ∥ ⃗ ) s i n θ , c o s θ v ⃗ ) e^{\hat{n}\theta}\cdot\vec{v_{\parallel}}=(-(\hat{u}\cdot\vec{v_{\parallel}})sin\theta,cos\theta\vec{v}) e n ^ θ ⋅ v ∥ = ( − ( u ^ ⋅ v ∥ ) s in θ , cos θ v ) 교환정리
이것도 나중에 써먹어야하니까 정리해둡니다.
근데 사실 내적코드라서 내적은 교환법칙이 성립하므로, 상관 없습니다.
v ∥ ⃗ ⋅ e r ^ θ = ( − ( v ∥ ⃗ ⋅ u ^ ) s i n θ , c o s θ v ⃗ ) ∴ e r ^ θ ⋅ v ∥ ⃗ = v ∥ ⃗ ⋅ e r ^ θ \vec{v_{\parallel}}\cdot e^{\hat{r}\theta} =(-(\vec{v_{\parallel}}\cdot\hat{u})sin\theta, cos\theta\vec{v})\\ \space \\ \therefore e^{\hat{r}\theta}\cdot\vec{v_{\parallel}}=\vec{v_{\parallel}}\cdot e^{\hat{r}\theta} v ∥ ⋅ e r ^ θ = ( − ( v ∥ ⋅ u ^ ) s in θ , cos θ v ) ∴ e r ^ θ ⋅ v ∥ = v ∥ ⋅ e r ^ θ 아무튼 최종적으로 둘을 정리하면
1차 회전정리 e n ^ θ ⋅ v ⃗ ↦ v ∥ ⃗ + e n ^ θ ⋅ v ⊥ ⃗ e^{\hat{n}\theta}\cdot\vec{v}\mapsto \vec{v_{\parallel}}+e^{\hat{n}\theta}\cdot\vec{v_{\perp}} e n ^ θ ⋅ v ↦ v ∥ + e n ^ θ ⋅ v ⊥ …mapsto가 맞을까요? 이건 정확히 모르겠네요
2차 회전정리 자 그런데 여기서 아까 반수성질 비슷한걸 쓴다고 했죠?
e n ^ ( θ 2 ) ⋅ e n ^ ( θ 2 ) = e n ^ θ e n ^ ( θ 2 ) ⋅ e n ^ ( − θ 2 ) = 1 e^{\hat{n}(\frac{\theta}{2})}\cdot e^{\hat{n}(\frac{\theta}{2})} =e^{\hat{n}\theta}\\ e^{\hat{n}(\frac{\theta}{2})}\cdot e^{\hat{n}(-\frac{\theta}{2})} =1 e n ^ ( 2 θ ) ⋅ e n ^ ( 2 θ ) = e n ^ θ e n ^ ( 2 θ ) ⋅ e n ^ ( − 2 θ ) = 1 두 식을 생각하여
v ∥ ⃗ + e n ^ θ ⋅ v ⊥ ⃗ = 1 ⋅ v ∥ ⃗ + e n ^ θ ⋅ v ⊥ ⃗ = e n ^ ( θ 2 ) ⋅ e n ^ ( − θ 2 ) ⋅ v ∥ ⃗ + e n ^ ( θ 2 ) ⋅ e n ^ ( θ 2 ) ⋅ v ⊥ ⃗ \vec{v_{\parallel}}+e^{\hat{n}\theta}\cdot\vec{v_{\perp}}=1\cdot\vec{v_{\parallel}}+e^{\hat{n}\theta}\cdot\vec{v_{\perp}}\\ =e^{\hat{n}(\frac{\theta}{2})}\cdot e^{\hat{n}(-\frac{\theta}{2})}\cdot\vec{v_{\parallel}}+e^{\hat{n}(\frac{\theta}{2})}\cdot e^{\hat{n}(\frac{\theta}{2})}\cdot\vec{v_{\perp}}\\ v ∥ + e n ^ θ ⋅ v ⊥ = 1 ⋅ v ∥ + e n ^ θ ⋅ v ⊥ = e n ^ ( 2 θ ) ⋅ e n ^ ( − 2 θ ) ⋅ v ∥ + e n ^ ( 2 θ ) ⋅ e n ^ ( 2 θ ) ⋅ v ⊥ 와 같이 나타낼 수 있습니다.
여기서 연산순서를 바꾸게 된다면,
평행벡터는 상관없음, 직교벡터는 부호반대 이므로
= e n ^ ( θ 2 ) ⋅ v ∥ ⃗ ⋅ e n ^ ( − θ 2 ) + e n ^ ( θ 2 ) ⋅ v ⊥ ⃗ ⋅ e n ^ ( − θ 2 ) = e n ^ ( θ 2 ) ⋅ ( v ∥ ⃗ + v ⊥ ⃗ ) ⋅ e n ^ ( − θ 2 ) = e n ^ ( θ 2 ) ⋅ ( v ⃗ ) ⋅ e n ^ ( − θ 2 ) =e^{\hat{n}(\frac{\theta}{2})}\cdot\vec{v_{\parallel}}\cdot e^{\hat{n}(-\frac{\theta}{2})}+e^{\hat{n}(\frac{\theta}{2})}\cdot\vec{v_{\perp}}\cdot e^{\hat{n}(-\frac{\theta}{2})}\\ =e^{\hat{n}(\frac{\theta}{2})}\cdot(\vec{v_{\parallel}}+\vec{v_{\perp}})\cdot e^{\hat{n}(-\frac{\theta}{2})}\\=e^{\hat{n}(\frac{\theta}{2})}\cdot(\vec{v})\cdot e^{\hat{n}(-\frac{\theta}{2})} = e n ^ ( 2 θ ) ⋅ v ∥ ⋅ e n ^ ( − 2 θ ) + e n ^ ( 2 θ ) ⋅ v ⊥ ⋅ e n ^ ( − 2 θ ) = e n ^ ( 2 θ ) ⋅ ( v ∥ + v ⊥ ) ⋅ e n ^ ( − 2 θ ) = e n ^ ( 2 θ ) ⋅ ( v ) ⋅ e n ^ ( − 2 θ ) 교환법칙이 외적의 반수성질과 유사하므로, 회전순서를 두번으로 분리하여, 곱의 순서를 바꿔 반대방향 회전이지만 반대의 반대로 회전하도록 꾀하는 것이죠.
와 놀랍습니다. 수학자들의 꼼수란…
정리 l e t , q = ( c o s θ 2 , u ^ ⋅ s i n θ 2 ) ∴ v ′ = q ⋅ v ⋅ q ∗ let, q=(cos\frac{\theta}{2},\hat{u}\cdot sin\frac{\theta}{2})\\ \therefore v'=q\cdot v\cdot q^*\\ l e t , q = ( cos 2 θ , u ^ ⋅ s in 2 θ ) ∴ v ′ = q ⋅ v ⋅ q ∗ 두 사원수의 곱은 각 사원수가 가진 각을 합한 사원수와의 곱임을 증명하시오 즉, 연속 회전한 결과라는것이죠?
q a ⋅ q b = q ( a + b ) ( c o s ( a ) , u ^ ⋅ s i n ( a ) ) ⋅ ( c o s ( b ) , u ^ ⋅ s i n ( b ) ) = = ( c o s ( a ) ⋅ c o s ( b ) − ( u ^ ⋅ s i n ( a ) ⋅ u ^ ⋅ s i n ( b ) ) , c o s ( a ) u ^ ⋅ s i n ( b ) + c o s ( b ) u ^ ⋅ s i n ( a ) + u ^ ⋅ s i n ( a ) × u ^ ⋅ s i n ( b ) ) q_{a}\cdot q_{b} = q_{(a+b)}\\ (cos(a),\hat{u}\cdot sin(a))\cdot (cos(b),\hat{u}\cdot sin(b)) = \\ =(cos(a)\cdot cos(b)-(\hat{u}\cdot sin(a)\cdot\hat{u}\cdot sin(b)),\\cos(a)\hat{u}\cdot sin(b)+cos(b)\hat{u}\cdot sin(a)+\hat{u}\cdot sin(a)\times\hat{u}\cdot sin(b))\\ q a ⋅ q b = q ( a + b ) ( cos ( a ) , u ^ ⋅ s in ( a )) ⋅ ( cos ( b ) , u ^ ⋅ s in ( b )) = = ( cos ( a ) ⋅ cos ( b ) − ( u ^ ⋅ s in ( a ) ⋅ u ^ ⋅ s in ( b )) , cos ( a ) u ^ ⋅ s in ( b ) + cos ( b ) u ^ ⋅ s in ( a ) + u ^ ⋅ s in ( a ) × u ^ ⋅ s in ( b )) 실수부 증명 cos ( a ) ⋅ cos ( b ) − ( u ^ ⋅ sin ( a ) ⋅ u ^ ⋅ sin ( b ) ) = cos ( a ) ⋅ cos ( b ) − ( u ^ ⋅ u ^ ⋅ sin ( a ) ⋅ sin ( b ) ) = cos ( a ) ⋅ cos ( b ) − ( 1 ⋅ sin ( a ) ⋅ sin ( b ) ) = cos ( ( a ) + ( b ) ) \cos(a)\cdot\cos(b)-(\hat{u}\cdot \sin(a)\cdot\hat{u}\cdot \sin(b))\\=\cos(a)\cdot\cos(b)-(\hat{u}\cdot \hat{u}\cdot \sin(a)\cdot\sin(b))\\=\cos(a)\cdot\cos(b)-(1\cdot\sin(a)\cdot\sin(b))\\=\cos((a)+(b)) cos ( a ) ⋅ cos ( b ) − ( u ^ ⋅ sin ( a ) ⋅ u ^ ⋅ sin ( b )) = cos ( a ) ⋅ cos ( b ) − ( u ^ ⋅ u ^ ⋅ sin ( a ) ⋅ sin ( b )) = cos ( a ) ⋅ cos ( b ) − ( 1 ⋅ sin ( a ) ⋅ sin ( b )) = cos (( a ) + ( b )) 허수부 증명 cos ( a ) u ^ ⋅ sin ( b ) + cos ( b ) u ^ ⋅ sin ( a ) + u ^ ⋅ sin ( a ) × u ^ ⋅ sin ( b ) = u ^ ⋅ ( cos ( a ) sin ( b ) + cos ( b ) sin ( a ) ) + u ^ × u ^ ⋅ ( sin ( a ) ⋅ sin ( b ) ) = u ^ ⋅ sin ( ( a ) + ( b ) ) + 0 = u ^ ⋅ sin ( ( a ) + ( b ) ) \cos(a)\hat{u}\cdot \sin(b)+\cos(b)\hat{u}\cdot \sin(a)+\hat{u}\cdot \sin(a)\times\hat{u}\cdot \sin(b)\\=\hat{u}\cdot (\cos(a)\sin(b)+\cos(b)\sin(a))+\hat{u}\times\hat{u}\cdot (\sin(a)\cdot\sin(b))\\=\hat{u}\cdot \sin((a)+(b))+0=\\ \hat{u}\cdot \sin((a)+(b)) cos ( a ) u ^ ⋅ sin ( b ) + cos ( b ) u ^ ⋅ sin ( a ) + u ^ ⋅ sin ( a ) × u ^ ⋅ sin ( b ) = u ^ ⋅ ( cos ( a ) sin ( b ) + cos ( b ) sin ( a )) + u ^ × u ^ ⋅ ( sin ( a ) ⋅ sin ( b )) = u ^ ⋅ sin (( a ) + ( b )) + 0 = u ^ ⋅ sin (( a ) + ( b )) 결국 삼각함수 공식으로 다 묶임을 볼 수 있으므로,
두 사원수의 곱은 각 사원수가 가진 각을 합한 사원수와의 곱임을 증명하였습니다.
3차원 공간에서의 회전 qvq*를 외적식으로 바꿔 표현하시오 와…………………………..
q v q ∗ = ( w , u ^ ) ⋅ ( 0 , v ⃗ ) ⋅ ( w , − u ^ ) = ( − ( u ^ ⋅ v ⃗ ) , w v ⃗ + u ^ × v ⃗ ) ⋅ ( w , − u ^ ) = ( − ( u ^ ⋅ v ⃗ ) w − ( w v ⃗ + u ^ × v ⃗ ) ⋅ ( − u ^ ) , − ( u ^ ⋅ v ⃗ ) ( − u ^ ) + w ( w v ⃗ + u ^ × v ⃗ ) + ( w v ⃗ + u ^ × v ⃗ ) × ( − u ^ ) ) qvq^*=(w,\hat{u})\cdot(0, \vec{v})\cdot(w,-\hat{u})\\=(-(\hat{u}\cdot\vec{v}),w\vec{v}+\hat{u}\times\vec{v})\cdot(w,-\hat{u})\\=(-(\hat{u}\cdot\vec{v})w-(w\vec{v}+\hat{u}\times\vec{v})\cdot(-\hat{u}),\\-(\hat{u}\cdot\vec{v})(-\hat{u})+w(w\vec{v}+\hat{u}\times\vec{v})+(w\vec{v}+\hat{u}\times\vec{v})\times(-\hat{u})) q v q ∗ = ( w , u ^ ) ⋅ ( 0 , v ) ⋅ ( w , − u ^ ) = ( − ( u ^ ⋅ v ) , w v + u ^ × v ) ⋅ ( w , − u ^ ) = ( − ( u ^ ⋅ v ) w − ( w v + u ^ × v ) ⋅ ( − u ^ ) , − ( u ^ ⋅ v ) ( − u ^ ) + w ( w v + u ^ × v ) + ( w v + u ^ × v ) × ( − u ^ )) 실수부 − w ( u ^ ⋅ v ⃗ ) − ( w v ⃗ + u ^ × v ⃗ ) ⋅ ( − u ^ ) = − w ( u ^ ⋅ v ⃗ ) + w ( v ⃗ ⋅ u ^ ) + ( u ^ × v ⃗ ) ⋅ u ^ = ( u ^ × v ⃗ ) ⋅ ( u ^ ) = 0 -w(\hat{u}\cdot\vec{v})-(w\vec{v}+\hat{u}\times\vec{v})\cdot(-\hat{u})\\=-w(\hat{u}\cdot\vec{v})+w(\vec{v}\cdot\hat{u})+(\hat{u}\times\vec{v})\cdot\hat{u}\\=(\hat{u} \times\vec{v})\cdot(\hat{u})=0 − w ( u ^ ⋅ v ) − ( w v + u ^ × v ) ⋅ ( − u ^ ) = − w ( u ^ ⋅ v ) + w ( v ⋅ u ^ ) + ( u ^ × v ) ⋅ u ^ = ( u ^ × v ) ⋅ ( u ^ ) = 0 허수부 − ( u ^ ⋅ v ⃗ ) ( − u ^ ) + w ( w v ⃗ + u ^ × v ⃗ ) + ( w v ⃗ + u ^ × v ⃗ ) × ( − u ^ ) = ( u ^ ⋅ v ⃗ ) u ^ + w 2 v ⃗ + w ( u ^ × v ⃗ ) − w ( v ⃗ × u ^ ) − ( u ^ × v ⃗ ) × ( u ^ ) -(\hat{u}\cdot\vec{v})(-\hat{u})+w(w\vec{v}+\hat{u}\times\vec{v})+(w\vec{v}+\hat{u}\times\vec{v})\times(-\hat{u})\\=(\hat{u}\cdot\vec{v})\hat{u}+w^2\vec{v}+w(\hat{u}\times\vec{v})-w(\vec{v}\times\hat{u})-(\hat{u}\times\vec{v})\times(\hat{u})\\ − ( u ^ ⋅ v ) ( − u ^ ) + w ( w v + u ^ × v ) + ( w v + u ^ × v ) × ( − u ^ ) = ( u ^ ⋅ v ) u ^ + w 2 v + w ( u ^ × v ) − w ( v × u ^ ) − ( u ^ × v ) × ( u ^ ) 여기서 묶을 수 있는게 보입니다.
단위사원수의 성질에 따라
단위사원수의 성질
w 2 + ∣ u ^ ∣ 2 = 1 w 2 = 1 − ∣ u ^ ∣ 2 w 2 = 1 − ( u ^ ⋅ u ^ ) w^2+\vert \hat{u}\vert ^2=1\\ w^2=1-\vert \hat{u}\vert ^2\\ w^2=1-(\hat{u}\cdot\hat{u}) w 2 + ∣ u ^ ∣ 2 = 1 w 2 = 1 − ∣ u ^ ∣ 2 w 2 = 1 − ( u ^ ⋅ u ^ ) 다시 대입하여 정리한다면 다음과 같은 꼴이 됩니다.
= ( u ^ ⋅ v ⃗ ) u ^ + w 2 v ⃗ + 2 w ( u ^ × v ⃗ ) + u ^ × ( u ^ × v ⃗ ) = ( u ^ ⋅ v ⃗ ) u ^ + w 2 v ⃗ + 2 w ( u ^ × v ⃗ ) + ( u ^ ⋅ v ⃗ ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v ⃗ = ( u ^ ⋅ v ⃗ ) u ^ + ( 1 − ( u ^ ⋅ u ^ ) ) v ⃗ + 2 w ( u ^ × v ⃗ ) + ( u ^ ⋅ v ⃗ ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v ⃗ = ( u ^ ⋅ v ⃗ ) u ^ + v ⃗ − ( u ^ ⋅ u ^ ) v ⃗ + 2 w ( u ^ × v ⃗ ) + ( u ^ ⋅ v ⃗ ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v ⃗ =(\hat{u}\cdot\vec{v})\hat{u}+w^2\vec{v}+2w(\hat{u}\times\vec{v})+\hat{u}\times(\hat{u}\times\vec{v})\\=(\hat{u}\cdot\vec{v})\hat{u}+w^2\vec{v}+2w(\hat{u}\times\vec{v})+(\hat{u}\cdot\vec{v})\cdot\hat{u}-(\hat{u}\cdot\hat{u})\cdot\vec{v} \\ \space \\ =(\hat{u}\cdot\vec{v})\hat{u}+(1-(\hat{u}\cdot\hat{u}))\vec{v}+2w(\hat{u}\times\vec{v})+(\hat{u}\cdot\vec{v})\cdot\hat{u}-(\hat{u}\cdot\hat{u})\cdot\vec{v}\\=(\hat{u}\cdot\vec{v})\hat{u}+\vec{v}-(\hat{u}\cdot\hat{u})\vec{v}+2w(\hat{u}\times\vec{v})+(\hat{u}\cdot\vec{v})\cdot\hat{u}-(\hat{u}\cdot\hat{u})\cdot\vec{v}\\ = ( u ^ ⋅ v ) u ^ + w 2 v + 2 w ( u ^ × v ) + u ^ × ( u ^ × v ) = ( u ^ ⋅ v ) u ^ + w 2 v + 2 w ( u ^ × v ) + ( u ^ ⋅ v ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v = ( u ^ ⋅ v ) u ^ + ( 1 − ( u ^ ⋅ u ^ )) v + 2 w ( u ^ × v ) + ( u ^ ⋅ v ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v = ( u ^ ⋅ v ) u ^ + v − ( u ^ ⋅ u ^ ) v + 2 w ( u ^ × v ) + ( u ^ ⋅ v ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v 여기서 이제 삼중곱의 부분들을 모두 정리해주면
= v ⃗ + 2 ( w ( u ^ × v ⃗ ) + ( u ^ ⋅ v ⃗ ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v ⃗ ) =\vec{v}+2(w(\hat{u}\times\vec{v})+(\hat{u}\cdot\vec{v})\cdot\hat{u}-(\hat{u}\cdot\hat{u})\cdot\vec{v}) = v + 2 ( w ( u ^ × v ) + ( u ^ ⋅ v ) ⋅ u ^ − ( u ^ ⋅ u ^ ) ⋅ v ) 앗 하나 더 있네요. 이것도 정리해줍니다.
= v ⃗ + 2 ( w ( u ^ × v ⃗ ) + u ^ × ( u ^ × v ⃗ ) ) = v ⃗ + 2 w ( u ^ × v ⃗ ) + 2 u ^ × ( u ^ × v ⃗ ) ) =\vec{v}+2(w(\hat{u}\times\vec{v})+\hat{u}\times(\hat{u}\times\vec{v}))\\ =\vec{v}+2w(\hat{u}\times\vec{v})+2\hat{u}\times(\hat{u}\times\vec{v})) = v + 2 ( w ( u ^ × v ) + u ^ × ( u ^ × v )) = v + 2 w ( u ^ × v ) + 2 u ^ × ( u ^ × v )) 그러면 묶이는게 보이죠?
l e t , t ⃗ = 2 ( u ^ × v ⃗ ) let, \vec{t} = 2(\hat{u} \times \vec{v}) \\ l e t , t = 2 ( u ^ × v ) 그러면 최종적으로 이렇게 됩니다
q v q ∗ = v ⃗ + w t ⃗ + u ^ × t ⃗ qvq^* = \vec{v}+w\vec{t}+\hat{u}\times\vec{t} q v q ∗ = v + w t + u ^ × t 3차원 공간에서의 회전 qvq*가 결국 로드리게스 회전공식과 동일함을 증명하시오. 그러면 로드리게스 공식부터 가져와야겠죠?
로드리게스 공식 ∴ u ′ ⃗ = cos θ ⋅ u ⃗ + ( 1 − c o s θ ) ⋅ ( u ⃗ ⋅ n ^ ) ⋅ n ^ + sin θ ⋅ ( n ^ × u ⃗ ) \therefore \vec{u^\prime}=\cos{\theta}\cdot\vec{u}+\left(1-cos{\theta}\right)\cdot\left(\vec{u}\cdot\hat{n}\right)\cdot\hat{n}+\sin{\theta}\cdot\left(\hat{n}\times\vec{u}\right) ∴ u ′ = cos θ ⋅ u + ( 1 − cos θ ) ⋅ ( u ⋅ n ^ ) ⋅ n ^ + sin θ ⋅ ( n ^ × u ) 여기서 축, n ^ \hat{n} n ^ u ^ \hat{u} u ^ u ⃗ \vec{u} u v ⃗ \vec{v} v
cos θ ⋅ v ⃗ + ( 1 − c o s θ ) ⋅ ( v ⃗ ⋅ u ^ ) ⋅ u ^ + sin θ ⋅ ( u ^ × v ⃗ ) \cos{\theta}\cdot\vec{v}+\left(1-cos{\theta}\right)\cdot\left(\vec{v}\cdot\hat{u}\right)\cdot\hat{u}+\sin{\theta}\cdot\left(\hat{u}\times\vec{v}\right) cos θ ⋅ v + ( 1 − cos θ ) ⋅ ( v ⋅ u ^ ) ⋅ u ^ + sin θ ⋅ ( u ^ × v ) …기존u와 현재u가 비슷하여 잘못 읽을 수 있겠네요
qvq* 회전 q v q ∗ = v ⃗ + 2 w ( u ^ × v ⃗ ) + 2 u ^ × ( u ^ × v ⃗ ) ) qvq^*=\vec{v}+2w(\hat{u}\times\vec{v})+2\hat{u}\times(\hat{u}\times\vec{v})) q v q ∗ = v + 2 w ( u ^ × v ) + 2 u ^ × ( u ^ × v )) 여기서
w = c o s θ 2 u ^ = u ^ ⋅ s i n θ 2 w=cos\frac{\theta}{2}\quad\quad\quad\hat{u}=\hat{u}\cdot sin\frac{\theta}{2}\quad w = cos 2 θ u ^ = u ^ ⋅ s in 2 θ 를 사용하게 된다면,
v ⃗ + 2 cos θ 2 ( u ^ × v ⃗ ) sin θ 2 + ( u ^ sin θ 2 × 2 ( u ^ sin θ 2 × v ⃗ ) ) = v ⃗ + 2 cos θ 2 sin θ 2 ( u ^ × v ⃗ ) + 2 sin 2 θ 2 ( u ^ × ( u ^ × v ⃗ ) ) \vec{v}+2\cos\frac{\theta}{2}(\hat{u}\times\vec{v})\sin\frac{\theta}{2}+(\hat{u}\sin\frac{\theta}{2}\times2(\hat{u}\sin\frac{\theta}{2}\times\vec{v}))\\=\vec{v}+2\cos\frac{\theta}{2}\sin\frac{\theta}{2}(\hat{u}\times\vec{v})+2\sin^2\frac{\theta}{2}(\hat{u}\times(\hat{u}\times\vec{v}))\\ v + 2 cos 2 θ ( u ^ × v ) sin 2 θ + ( u ^ sin 2 θ × 2 ( u ^ sin 2 θ × v )) = v + 2 cos 2 θ sin 2 θ ( u ^ × v ) + 2 sin 2 2 θ ( u ^ × ( u ^ × v )) 이렇게 나오게 되는데, 이를 다시 삼각함수를 변형하여
캐시된 삼각함수
s i n ( x + y ) = s i n ( x ) c o s ( y ) + c o s ( x ) s i n ( y ) s i n ( x − y ) = s i n ( x ) c o s ( y ) − c o s ( x ) s i n ( y ) c o s ( x + y ) = c o s ( x ) c o s ( y ) − s i n ( x ) s i n ( y ) c o s ( x − y ) = c o s ( x ) c o s ( y ) + s i n ( x ) s i n ( y ) s i n ( x ) + s i n ( y ) = 2 s i n ( x + y 2 ) c o s ( x − y 2 ) s i n ( x ) − s i n ( y ) = 2 c o s ( x + y 2 ) s i n ( x − y 2 ) c o s ( x ) + c o s ( y ) = 2 c o s ( x + y 2 ) c o s ( x − y 2 ) c o s ( x ) − c o s ( y ) = − 2 s i n ( x + y 2 ) 2 s i n ( x − y 2 ) s i n ( x ) c o s ( y ) = 1 2 ( s i n ( x + y ) + s i n ( x − y ) ) c o s ( x ) s i n ( y ) = 1 2 ( s i n ( x + y ) − s i n ( x − y ) ) c o s ( x ) c o s ( y ) = 1 2 ( c o s ( x + y ) + c o s ( x − y ) ) s i n ( x ) s i n ( y ) = − 1 2 ( c o s ( x + y ) − c o s ( x − y ) ) s i n ( x + y ) − s i n ( x − y ) = 2 c o s ( x ) s i n ( y ) sin 2 θ 2 = 1 − cos θ 2 . . . sin(x+y) = sin(x)cos(y)+cos(x)sin(y)\\sin(x-y) = sin(x)cos(y)-cos(x)sin(y)\\cos(x+y) = cos(x)cos(y)-sin(x)sin(y)\\cos(x-y) = cos(x)cos(y)+sin(x)sin(y)\\\\\quad\\sin(x) + sin(y) = 2sin(\frac{x+y}{2})cos(\frac{x-y}{2})\\sin(x) - sin(y) = 2cos(\frac{x+y}{2})sin(\frac{x-y}{2})\\cos(x) + cos(y) = 2cos(\frac{x+y}{2})cos(\frac{x-y}{2})\\cos(x) - cos(y) = -2sin(\frac{x+y}{2})2sin(\frac{x-y}{2})\\\\\quad\\ sin(x)cos(y) = \frac{1}{2}(sin(x+y)+sin(x-y))\\cos(x)sin(y) =\frac{1}{2}(sin(x+y)-sin(x-y))\\cos(x)cos(y) = \frac{1}{2}(cos(x+y)+cos(x-y))\\sin(x)sin(y) = -\frac{1}{2}(cos(x+y)-cos(x-y))\\ \\\quad\\ sin(x+y) - sin(x-y) = 2cos(x) sin(y)\\ \sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2} \\... s in ( x + y ) = s in ( x ) cos ( y ) + cos ( x ) s in ( y ) s in ( x − y ) = s in ( x ) cos ( y ) − cos ( x ) s in ( y ) cos ( x + y ) = cos ( x ) cos ( y ) − s in ( x ) s in ( y ) cos ( x − y ) = cos ( x ) cos ( y ) + s in ( x ) s in ( y ) s in ( x ) + s in ( y ) = 2 s in ( 2 x + y ) cos ( 2 x − y ) s in ( x ) − s in ( y ) = 2 cos ( 2 x + y ) s in ( 2 x − y ) cos ( x ) + cos ( y ) = 2 cos ( 2 x + y ) cos ( 2 x − y ) cos ( x ) − cos ( y ) = − 2 s in ( 2 x + y ) 2 s in ( 2 x − y ) s in ( x ) cos ( y ) = 2 1 ( s in ( x + y ) + s in ( x − y )) cos ( x ) s in ( y ) = 2 1 ( s in ( x + y ) − s in ( x − y )) cos ( x ) cos ( y ) = 2 1 ( cos ( x + y ) + cos ( x − y )) s in ( x ) s in ( y ) = − 2 1 ( cos ( x + y ) − cos ( x − y )) s in ( x + y ) − s in ( x − y ) = 2 cos ( x ) s in ( y ) sin 2 2 θ = 2 1 − cos θ ... = v ⃗ + ( sin θ − sin 0 ) ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( u ^ × ( u ^ × v ⃗ ) ) = v ⃗ + sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( u ^ × ( u ^ × v ⃗ ) ) =\vec{v}+(\sin\theta-\sin0)\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot(\hat{u}\times(\hat{u}\times\vec{v}))\\=\vec{v}+\sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot(\hat{u}\times(\hat{u}\times\vec{v})) = v + ( sin θ − sin 0 ) ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ ( u ^ × ( u ^ × v )) = v + sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ ( u ^ × ( u ^ × v )) 아까 벡터 삼중곱으로 묶었던 부분도 다시 풀어줍시다
v ⃗ + sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( ( u ^ ⋅ ( u ^ ⋅ v ⃗ ) − v ⃗ ⋅ ( u ^ ⋅ u ^ ) ) = v ⃗ + sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( ( u ^ ⋅ ( u ^ ⋅ v ⃗ ) − v ⃗ ) = v ⃗ + sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v ⃗ ) ) − v ⃗ + v ⃗ cos θ = sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v ⃗ ) ) + v ⃗ cos θ \vec{v}+\sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot((\hat{u}\cdot(\hat{u}\cdot\vec{v})-\vec{v}\cdot(\hat{u}\cdot\hat{u}))\\=\vec{v}+\sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot((\hat{u}\cdot(\hat{u}\cdot\vec{v})-\vec{v})\\ =\vec{v}+\sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot(\hat{u}\cdot(\hat{u}\cdot\vec{v}))-\vec{v}+\vec{v}\cos\theta\\ =\sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot(\hat{u}\cdot(\hat{u}\cdot\vec{v}))+\vec{v}\cos\theta v + sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ (( u ^ ⋅ ( u ^ ⋅ v ) − v ⋅ ( u ^ ⋅ u ^ )) = v + sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ (( u ^ ⋅ ( u ^ ⋅ v ) − v ) = v + sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v )) − v + v cos θ = sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v )) + v cos θ 비교 cos θ ⋅ v ⃗ + ( 1 − c o s θ ) ⋅ ( v ⃗ ⋅ u ^ ) ⋅ u ^ + sin θ ⋅ ( u ^ × v ⃗ ) \cos{\theta}\cdot\vec{v}+\left(1-cos{\theta}\right)\cdot\left(\vec{v}\cdot\hat{u}\right)\cdot\hat{u}+\sin{\theta}\cdot\left(\hat{u}\times\vec{v}\right) cos θ ⋅ v + ( 1 − cos θ ) ⋅ ( v ⋅ u ^ ) ⋅ u ^ + sin θ ⋅ ( u ^ × v ) sin θ ⋅ ( u ^ × v ⃗ ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v ⃗ ) ) + v ⃗ cos θ \sin\theta\cdot(\hat{u}\times\vec{v})+(1-\cos\theta)\cdot(\hat{u}\cdot(\hat{u}\cdot\vec{v}))+\vec{v}\cos\theta sin θ ⋅ ( u ^ × v ) + ( 1 − cos θ ) ⋅ ( u ^ ⋅ ( u ^ ⋅ v )) + v cos θ 어때요, 교환법칙이 성립하므로, 순서만 바꾸면 똑같죠?
사원수의 변환 저는 잘 모르겠습니다 여기를 확인해 주세요…………………….
https://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/index.htm
사원수에서 회전 행렬 간단합니다.
사원수에서 회전행렬로 변환해야한다면,
단순히 세 기저벡터를 사원수와 곱해, 변환된 벡터로 행렬을 구성하면 됩니다.
…말만 쉽습니다. 이걸 21세기에 손으로 직접… 인간이 직접 계산해야 할 줄은 몰랐습니다…
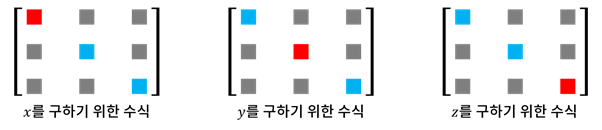
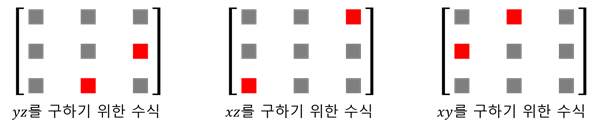
정의 x ⃗ = q ⋅ ( 1 , 0 , 0 ) ⋅ q ∗ y ⃗ = q ⋅ ( 0 , 1 , 0 ) ⋅ q ∗ z ⃗ = q ⋅ ( 0 , 0 , 1 ) ⋅ q ∗ q = ( w , ( x ′ , y ′ , z ′ ) ) \vec{x}=q\cdot(1,0,0)\cdot q^*\\ \vec{y}=q\cdot(0,1,0)\cdot q^*\\ \vec{z}=q\cdot(0,0,1)\cdot q^*\\ \space \\ q=(w, (x',y',z')) x = q ⋅ ( 1 , 0 , 0 ) ⋅ q ∗ y = q ⋅ ( 0 , 1 , 0 ) ⋅ q ∗ z = q ⋅ ( 0 , 0 , 1 ) ⋅ q ∗ q = ( w , ( x ′ , y ′ , z ′ )) 계산 X축
x = ( 1 , 0 , 0 ) + 2 w ( ( x ′ , y ′ , z ′ ) × ( 1 , 0 , 0 ) ) + ( ( x ′ , y ′ , z ′ ) × 2 ( ( x ′ , y ′ , z ′ ) × ( 1 , 0 , 0 ) ) = ( 1 , 0 , 0 ) + 2 w ( 0 , z ′ , − y ′ ) + 2 ( ( x ′ , y ′ , z ′ ) × ( 0 , z ′ , − y ′ ) ) = ( 1 , 0 , 0 ) + ( 0 , 2 w z ′ , − 2 w y ′ ) + 2 ( − y ′ 2 − z ′ 2 , x ′ y ′ , x ′ z ′ ) = ( 1 , 0 , 0 ) + ( 0 , 2 w z ′ , − 2 w y ′ ) + ( − 2 y ′ 2 − 2 z ′ 2 , 2 x ′ y ′ , 2 x ′ z ′ ) = ( 1 − 2 y ′ 2 − 2 z ′ 2 , 2 w z ′ + 2 x ′ y ′ , 2 x ′ z ′ − 2 w y ′ ) = ( 1 − 2 ( y ′ 2 + z ′ 2 ) , 2 ( x ′ y ′ + w z ′ ) , 2 ( x ′ z ′ − w y ′ ) ) x=(1,0,0)+2w((x′,y′,z′)×(1,0,0))+((x′,y′,z′)×2((x′,y′,z′)×(1,0,0))=(1,0,0)+2w(0,z′,−y′)+2((x′,y′,z′)×(0,z′,−y′))=(1,0,0)+(0,2wz′,−2wy′)+2(−y′2−z′2,x′y′,x′z′)=(1,0,0)+(0,2wz′,−2wy′)+(−2y′2−2z′2,2x′y′,2x′z′)=(1−2y′2−2z′2,2wz′+2x′y′,2x′z′−2wy′)=(1−2(y′2+z′2),2(x′y′+wz′),2(x′z′−wy′)) x = ( 1 , 0 , 0 ) + 2 w (( x ′ , y ′ , z ′ ) × ( 1 , 0 , 0 )) + (( x ′ , y ′ , z ′ ) × 2 (( x ′ , y ′ , z ′ ) × ( 1 , 0 , 0 )) = ( 1 , 0 , 0 ) + 2 w ( 0 , z ′ , − y ′ ) + 2 (( x ′ , y ′ , z ′ ) × ( 0 , z ′ , − y ′ )) = ( 1 , 0 , 0 ) + ( 0 , 2 w z ′ , − 2 w y ′ ) + 2 ( − y ′2 − z ′2 , x ′ y ′ , x ′ z ′ ) = ( 1 , 0 , 0 ) + ( 0 , 2 w z ′ , − 2 w y ′ ) + ( − 2 y ′2 − 2 z ′2 , 2 x ′ y ′ , 2 x ′ z ′ ) = ( 1 − 2 y ′2 − 2 z ′2 , 2 w z ′ + 2 x ′ y ′ , 2 x ′ z ′ − 2 w y ′ ) = ( 1 − 2 ( y ′2 + z ′2 ) , 2 ( x ′ y ′ + w z ′ ) , 2 ( x ′ z ′ − w y ′ )) Y축
y ⃗ = ( 0 , 1 , 0 ) + 2 w ( ( x ′ , y ′ , z ′ ) × ( 0 , 1 , 0 ) ) + ( ( x ′ , y ′ , z ′ ) × 2 ( ( x ′ , y ′ , z ′ ) × ( 0 , 1 , 0 ) ) = ( 0 , 1 , 0 ) + 2 w ( − z ′ , 0 , x ′ ) + 2 ( ( x ′ , y ′ , z ′ ) × ( − z ′ , 0 , x ′ ) ) = ( 0 , 1 , 0 ) + ( − 2 w z ′ , 0 , 2 w x ′ ) + 2 ( y ′ x ′ , − z ′ 2 − x ′ 2 , y ′ z ′ ) = ( 0 , 1 , 0 ) + ( − 2 w z ′ , 0 , 2 w x ′ ) + ( 2 y ′ x ′ , − 2 z ′ 2 − 2 x ′ 2 , 2 y ′ z ′ ) = ( 2 y ′ x ′ − 2 w z ′ , 1 − 2 z ′ 2 − 2 x ′ 2 , 2 w x ′ + 2 y ′ z ′ ) = ( 2 ( x ′ y ′ − w z ′ ) , 1 − 2 ( x ′ 2 + z ′ 2 ) , 2 ( y ′ z ′ + w x ′ ) ) \vec{y}=(0,1,0)+2w((x',y',z')\times(0,1,0))+((x',y',z')\times2((x',y',z')\times(0,1,0))\\ =(0,1,0)+2w(-z',0,x')+2((x',y',z')\times(-z',0,x'))\\ =(0,1,0)+(-2wz',0,2wx')+2(y'x',-z'^2-x'^2,y'z')\\ =(0,1,0)+(-2wz',0,2wx')+(2y'x',-2z'^2-2x'^2,2y'z')\\ =(2y'x'-2wz',1-2z'^2-2x'^2,2wx'+2y'z')\\ =(2(x'y'-wz'),1-2(x'^2+z'^2),2(y'z'+wx')) y = ( 0 , 1 , 0 ) + 2 w (( x ′ , y ′ , z ′ ) × ( 0 , 1 , 0 )) + (( x ′ , y ′ , z ′ ) × 2 (( x ′ , y ′ , z ′ ) × ( 0 , 1 , 0 )) = ( 0 , 1 , 0 ) + 2 w ( − z ′ , 0 , x ′ ) + 2 (( x ′ , y ′ , z ′ ) × ( − z ′ , 0 , x ′ )) = ( 0 , 1 , 0 ) + ( − 2 w z ′ , 0 , 2 w x ′ ) + 2 ( y ′ x ′ , − z ′2 − x ′2 , y ′ z ′ ) = ( 0 , 1 , 0 ) + ( − 2 w z ′ , 0 , 2 w x ′ ) + ( 2 y ′ x ′ , − 2 z ′2 − 2 x ′2 , 2 y ′ z ′ ) = ( 2 y ′ x ′ − 2 w z ′ , 1 − 2 z ′2 − 2 x ′2 , 2 w x ′ + 2 y ′ z ′ ) = ( 2 ( x ′ y ′ − w z ′ ) , 1 − 2 ( x ′2 + z ′2 ) , 2 ( y ′ z ′ + w x ′ )) Z축
z ⃗ = ( 0 , 0 , 1 ) + 2 w ( ( x ′ , y ′ , z ′ ) × ( 0 , 0 , 1 ) ) + ( ( x ′ , y ′ , z ′ ) × 2 ( ( x ′ , y ′ , z ′ ) × ( 0 , 0 , 1 ) ) = ( 0 , 0 , 1 ) + 2 w ( y ′ , − x ′ , 0 ) + 2 ( ( x ′ , y ′ , z ′ ) × ( y ′ , − x ′ , 0 ) ) = ( 0 , 0 , 1 ) + ( 2 w y ′ , − 2 w x ′ , 0 ) + 2 ( z ′ x ′ , z ′ y ′ , − x ′ 2 − y ′ 2 ) = ( 0 , 0 , 1 ) + ( 2 w y ′ , − 2 w x ′ , 0 ) + ( 2 z ′ x ′ , 2 z ′ y ′ , − 2 x ′ 2 − 2 y ′ 2 ) = ( 2 z ′ x ′ + 2 w y ′ , 2 z ′ y ′ − 2 w x ′ , 1 − 2 x ′ 2 − 2 y ′ 2 ) = ( 2 ( x ′ z ′ + w y ′ ) , 2 ( y ′ z ′ − w x ′ ) , 1 − 2 ( x ′ 2 + y ′ 2 ) ) \vec{z}=(0,0,1)+2w((x',y',z')\times(0,0,1))+((x',y',z')\times2((x',y',z')\times(0,0,1))\\ =(0,0,1)+2w(y',-x',0)+2((x',y',z')\times(y',-x',0))\\ =(0,0,1)+(2wy',-2wx',0)+2(z'x',z'y',-x'^2-y'^2)\\ =(0,0,1)+(2wy',-2wx',0)+(2z'x',2z'y',-2x'^2-2y'^2)\\ =(2z'x'+2wy',2z'y'-2wx',1-2x'^2-2y'^2)\\ =(2(x'z'+wy'),2(y'z'-wx'),1-2(x'^2+y'^2)) z = ( 0 , 0 , 1 ) + 2 w (( x ′ , y ′ , z ′ ) × ( 0 , 0 , 1 )) + (( x ′ , y ′ , z ′ ) × 2 (( x ′ , y ′ , z ′ ) × ( 0 , 0 , 1 )) = ( 0 , 0 , 1 ) + 2 w ( y ′ , − x ′ , 0 ) + 2 (( x ′ , y ′ , z ′ ) × ( y ′ , − x ′ , 0 )) = ( 0 , 0 , 1 ) + ( 2 w y ′ , − 2 w x ′ , 0 ) + 2 ( z ′ x ′ , z ′ y ′ , − x ′2 − y ′2 ) = ( 0 , 0 , 1 ) + ( 2 w y ′ , − 2 w x ′ , 0 ) + ( 2 z ′ x ′ , 2 z ′ y ′ , − 2 x ′2 − 2 y ′2 ) = ( 2 z ′ x ′ + 2 w y ′ , 2 z ′ y ′ − 2 w x ′ , 1 − 2 x ′2 − 2 y ′2 ) = ( 2 ( x ′ z ′ + w y ′ ) , 2 ( y ′ z ′ − w x ′ ) , 1 − 2 ( x ′2 + y ′2 )) 행렬로 나타내면 이렇습니다신하고싶지않습니다
[ 1 − 2 ( y ′ 2 + z ′ 2 ) 2 ( x ′ y ′ − w z ′ ) 2 ( x ′ z ′ + w y ′ ) 0 2 ( x ′ y ′ + w z ′ ) 1 − 2 ( x ′ 2 + z ′ 2 ) 2 ( y ′ z ′ − w x ′ ) 0 2 ( x ′ z ′ − w y ′ ) 2 ( y ′ z ′ + w x ′ ) 1 − 2 ( x ′ 2 + y ′ 2 ) 0 0 0 0 1 ] \left[\begin{matrix} 1-2(y'^2+z'^2)&2(x'y'-wz')&2(x'z'+wy')&0\\ 2(x'y'+wz')&1-2(x'^2+z'^2)&2(y'z'-wx')&0\\ 2(x'z'-wy')&2(y'z'+wx')&1-2(x'^2+y'^2)&0\\ 0&0&0&1 \\\end{matrix}\right] 1 − 2 ( y ′2 + z ′2 ) 2 ( x ′ y ′ + w z ′ ) 2 ( x ′ z ′ − w y ′ ) 0 2 ( x ′ y ′ − w z ′ ) 1 − 2 ( x ′2 + z ′2 ) 2 ( y ′ z ′ + w x ′ ) 0 2 ( x ′ z ′ + w y ′ ) 2 ( y ′ z ′ − w x ′ ) 1 − 2 ( x ′2 + y ′2 ) 0 0 0 0 1 사원수에서 오일러 각 여기서부터 대략 정신이 멍해집니다.
후…
캐시된 삼각함수
s i n ( x + y ) = s i n ( x ) c o s ( y ) + c o s ( x ) s i n ( y ) s i n ( x − y ) = s i n ( x ) c o s ( y ) − c o s ( x ) s i n ( y ) c o s ( x + y ) = c o s ( x ) c o s ( y ) − s i n ( x ) s i n ( y ) c o s ( x − y ) = c o s ( x ) c o s ( y ) + s i n ( x ) s i n ( y ) s i n ( x ) + s i n ( y ) = 2 s i n ( x + y 2 ) c o s ( x − y 2 ) s i n ( x ) − s i n ( y ) = 2 c o s ( x + y 2 ) s i n ( x − y 2 ) c o s ( x ) + c o s ( y ) = 2 c o s ( x + y 2 ) c o s ( x − y 2 ) c o s ( x ) − c o s ( y ) = − 2 s i n ( x + y 2 ) 2 s i n ( x − y 2 ) s i n ( x ) c o s ( y ) = 1 2 ( s i n ( x + y ) + s i n ( x − y ) ) c o s ( x ) s i n ( y ) = 1 2 ( s i n ( x + y ) − s i n ( x − y ) ) c o s ( x ) c o s ( y ) = 1 2 ( c o s ( x + y ) + c o s ( x − y ) ) s i n ( x ) s i n ( y ) = − 1 2 ( c o s ( x + y ) − c o s ( x − y ) ) s i n ( x + y ) − s i n ( x − y ) = 2 c o s ( x ) s i n ( y ) sin 2 θ 2 = 1 − cos θ 2 . . . sin(x+y) = sin(x)cos(y)+cos(x)sin(y)\\sin(x-y) = sin(x)cos(y)-cos(x)sin(y)\\cos(x+y) = cos(x)cos(y)-sin(x)sin(y)\\cos(x-y) = cos(x)cos(y)+sin(x)sin(y)\\\\\quad\\sin(x) + sin(y) = 2sin(\frac{x+y}{2})cos(\frac{x-y}{2})\\sin(x) - sin(y) = 2cos(\frac{x+y}{2})sin(\frac{x-y}{2})\\cos(x) + cos(y) = 2cos(\frac{x+y}{2})cos(\frac{x-y}{2})\\cos(x) - cos(y) = -2sin(\frac{x+y}{2})2sin(\frac{x-y}{2})\\\\\quad\\ sin(x)cos(y) = \frac{1}{2}(sin(x+y)+sin(x-y))\\cos(x)sin(y) =\frac{1}{2}(sin(x+y)-sin(x-y))\\cos(x)cos(y) = \frac{1}{2}(cos(x+y)+cos(x-y))\\sin(x)sin(y) = -\frac{1}{2}(cos(x+y)-cos(x-y))\\ \\\quad\\ sin(x+y) - sin(x-y) = 2cos(x) sin(y)\\ \sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2} \\... s in ( x + y ) = s in ( x ) cos ( y ) + cos ( x ) s in ( y ) s in ( x − y ) = s in ( x ) cos ( y ) − cos ( x ) s in ( y ) cos ( x + y ) = cos ( x ) cos ( y ) − s in ( x ) s in ( y ) cos ( x − y ) = cos ( x ) cos ( y ) + s in ( x ) s in ( y ) s in ( x ) + s in ( y ) = 2 s in ( 2 x + y ) cos ( 2 x − y ) s in ( x ) − s in ( y ) = 2 cos ( 2 x + y ) s in ( 2 x − y ) cos ( x ) + cos ( y ) = 2 cos ( 2 x + y ) cos ( 2 x − y ) cos ( x ) − cos ( y ) = − 2 s in ( 2 x + y ) 2 s in ( 2 x − y ) s in ( x ) cos ( y ) = 2 1 ( s in ( x + y ) + s in ( x − y )) cos ( x ) s in ( y ) = 2 1 ( s in ( x + y ) − s in ( x − y )) cos ( x ) cos ( y ) = 2 1 ( cos ( x + y ) + cos ( x − y )) s in ( x ) s in ( y ) = − 2 1 ( cos ( x + y ) − cos ( x − y )) s in ( x + y ) − s in ( x − y ) = 2 cos ( x ) s in ( y ) sin 2 2 θ = 2 1 − cos θ ... θ y a w = 2 ( w y + x z ) 1 − 2 ( x 2 + y 2 ) \theta_{yaw}=\frac{2(wy+xz)}{1-2(x^2+y^2)} θ y a w = 1 − 2 ( x 2 + y 2 ) 2 ( w y + x z ) a t a n 2 ( 2 ( w x ′ + y ′ z ′ ) , 1 − 2 ( x ′ 2 + y ′ 2 ) = θ y a w a s i n ( 2 ( w y ′ − z ′ x ′ ) ) = θ p i t c h a t a n 2 ( 2 ( w z ′ + x ′ y ′ , 1 − 2 ( y ′ 2 + z ′ 2 ) ) = θ r o l l \begin{align*} atan2(2(wx'+y'z'), 1-2(x'^2+y'^2)=\theta_{yaw}\\ asin(2(wy'-z'x'))=\theta_{pitch}\\ atan2(2(wz'+x'y', 1-2(y'^2+z'^2)) =\theta_{roll}\\ \end{align*} a t an 2 ( 2 ( w x ′ + y ′ z ′ ) , 1 − 2 ( x ′2 + y ′2 ) = θ y a w a s in ( 2 ( w y ′ − z ′ x ′ )) = θ p i t c h a t an 2 ( 2 ( w z ′ + x ′ y ′ , 1 − 2 ( y ′2 + z ′2 )) = θ ro ll 저는 도저히 이해를 하지 못해 추가적인 코드들을 첨부하였습니다.
사원수 → 오일러각 (1) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static Vector3 FromQ2 ( Quaternion q1 )
{
float sqw = q1 . w * q1 . w ;
float sqx = q1 . x * q1 . x ;
float sqy = q1 . y * q1 . y ;
float sqz = q1 . z * q1 . z ;
float unit = sqx + sqy + sqz + sqw ; // if normalised is one, otherwise is correction factor
float test = q1 . x * q1 . w - q1 . y * q1 . z ;
Vector3 v ;
if ( test > 0.4995f * unit ) { // singularity at north pole
v . y = 2f * Mathf . Atan2 ( q1 . y , q1 . x );
v . x = Mathf . PI / 2 ;
v . z = 0 ;
return NormalizeAngles ( v * Mathf . Rad2Deg );
}
if ( test < - 0.4995f * unit ) { // singularity at south pole
v . y = - 2f * Mathf . Atan2 ( q1 . y , q1 . x );
v . x = - Mathf . PI / 2 ;
v . z = 0 ;
return NormalizeAngles ( v * Mathf . Rad2Deg );
}
Quaternion q = new Quaternion ( q1 . w , q1 . z , q1 . x , q1 . y );
v . y = ( float ) Math . Atan2 ( 2f * q . x * q . w + 2f * q . y * q . z , 1 - 2f * ( q . z * q . z + q . w * q . w )); // Yaw
v . x = ( float ) Math . Asin ( 2f * ( q . x * q . z - q . w * q . y )); // Pitch
v . z = ( float ) Math . Atan2 ( 2f * q . x * q . y + 2f * q . z * q . w , 1 - 2f * ( q . y * q . y + q . z * q . z )); // Roll
return NormalizeAngles ( v * Mathf . Rad2Deg );
}
사원수 → 오일러각 (2) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def euler_from_quaternion ( x , y , z , w ):
"""
Convert a quaternion into euler angles (roll, pitch, yaw)
roll is rotation around x in radians (counterclockwise)
pitch is rotation around y in radians (counterclockwise)
yaw is rotation around z in radians (counterclockwise)
"""
t0 = + 2.0 * ( w * x + y * z )
t1 = + 1.0 - 2.0 * ( x * x + y * y )
roll_x = math . atan2 ( t0 , t1 )
t2 = + 2.0 * ( w * y - z * x )
t2 = + 1.0 if t2 > + 1.0 else t2
t2 = - 1.0 if t2 < - 1.0 else t2
pitch_y = math . asin ( t2 )
t3 = + 2.0 * ( w * z + x * y )
t4 = + 1.0 - 2.0 * ( y * y + z * z )
yaw_z = math . atan2 ( t3 , t4 )
return roll_x , pitch_y , yaw_z
사원수 → 오일러각 (3) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
FRotator FQuat :: Rotator () const
{
const float SingularityTest = Z * X - W * Y ;
const float YawY = 2. f * ( W * Z + X * Y );
const float YawX = ( 1. f - 2. f * ( FMath :: Square ( Y ) + FMath :: Square ( Z )));
// reference
// http://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
// http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/
// this value was found from experience, the above websites recommend different values
// but that isn't the case for us, so I went through different testing, and finally found the case
// where both of world lives happily.
const float SINGULARITY_THRESHOLD = 0.4999995 f ;
const float RAD_TO_DEG = ( 180. f ) / PI ;
FRotator RotatorFromQuat ;
if ( SingularityTest < - SINGULARITY_THRESHOLD )
{
RotatorFromQuat . Pitch = - 90. f ;
RotatorFromQuat . Yaw = FMath :: Atan2 ( YawY , YawX ) * RAD_TO_DEG ;
RotatorFromQuat . Roll = FRotator :: NormalizeAxis ( - RotatorFromQuat . Yaw - ( 2. f * FMath :: Atan2 ( X , W ) * RAD_TO_DEG ));
}
else if ( SingularityTest > SINGULARITY_THRESHOLD )
{
RotatorFromQuat . Pitch = 90. f ;
RotatorFromQuat . Yaw = FMath :: Atan2 ( YawY , YawX ) * RAD_TO_DEG ;
RotatorFromQuat . Roll = FRotator :: NormalizeAxis ( RotatorFromQuat . Yaw - ( 2. f * FMath :: Atan2 ( X , W ) * RAD_TO_DEG ));
}
else
{
RotatorFromQuat . Pitch = FMath :: FastAsin ( 2. f * ( SingularityTest )) * RAD_TO_DEG ;
RotatorFromQuat . Yaw = FMath :: Atan2 ( YawY , YawX ) * RAD_TO_DEG ;
RotatorFromQuat . Roll = FMath :: Atan2 ( - 2. f * ( W * X + Y * Z ), ( 1. f - 2. f * ( FMath :: Square ( X ) + FMath :: Square ( Y )))) * RAD_TO_DEG ;
}
return RotatorFromQuat ;
}
오일러 각에서 사원수 q r o l l = cos θ r o l l 2 + sin θ r o l l 2 k q p i t c h = cos θ p i t c h 2 + sin θ p i t c h 2 i q y a w = cos θ y a w 2 + sin θ y a w 2 j q_{roll}=\cos\frac{\theta_{roll}}{2}+\sin\frac{\theta_{roll}}{2}k\\ q_{pitch}=\cos\frac{\theta_{pitch}}{2}+\sin\frac{\theta_{pitch}}{2}i\\ q_{yaw}=\cos\frac{\theta_{yaw}}{2}+\sin\frac{\theta_{yaw}}{2}j q ro ll = cos 2 θ ro ll + sin 2 θ ro ll k q p i t c h = cos 2 θ p i t c h + sin 2 θ p i t c h i q y a w = cos 2 θ y a w + sin 2 θ y a w j 여전히 마찬가지로 회전순서를 잘 해야합니다.
Roll → Pitch → Yaw 순으로 회전을 적용하지만
열기반 행렬로 사용하므로 Yaw → Pitch → Roll 순으로 배치하여 계산해야합니다.
q y a w ⋅ q p i t c h ⋅ q r o l l = ( cos θ y a w 2 , sin θ y a w 2 j ) ⋅ ( cos θ p i t c h 2 , sin θ p i t c h 2 i ) ⋅ ( cos θ r o l l 2 , sin θ r o l l 2 k ) = ( cos θ y a w 2 , sin θ y a w 2 j ) ⋅ ( cos θ p i t c h 2 cos θ r o l l 2 , cos θ p i t c h 2 sin θ r o l l 2 k + cos θ r o l l 2 sin θ p i t c h 2 i − ( sin θ p i t c h 2 sin θ r o l l 2 ) j ) = ( cos θ y a w 2 cos θ p i t c h 2 cos θ r o l l 2 + sin θ y a w 2 sin θ p i t c h 2 sin θ r o l l 2 , cos θ y a w 2 ( cos θ p i t c h 2 sin θ r o l l 2 k + cos θ r o l l 2 sin θ p i t c h 2 i − ( sin θ p i t c h 2 sin θ r o l l 2 ) j ) + cos θ p i t c h 2 cos θ r o l l 2 ( sin θ y a w 2 j ) + ( sin θ y a w 2 cos θ p i t c h 2 sin θ r o l l 2 ) i − ( sin θ y a w 2 cos θ r o l l 2 sin θ p i t c h 2 ) k ) q_{yaw}\cdot q_{pitch}\cdot q_{roll}\\ =(\cos\frac{\theta_{yaw}}{2},\sin\frac{\theta_{yaw}}{2}j)\cdot(\cos\frac{\theta_{pitch}}{2},\sin\frac{\theta_{pitch}}{2}i)\cdot(\cos\frac{\theta_{roll}}{2},\sin\frac{\theta_{roll}}{2}k)\\ \space\\ =(\cos\frac{\theta_{yaw}}{2},\sin\frac{\theta_{yaw}}{2}j)\cdot(\cos\frac{\theta_{pitch}}{2}\cos\frac{\theta_{roll}}{2},\cos\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2}k+\cos\frac{\theta_{roll}}{2}\sin\frac{\theta_{pitch}}{2}i-(\sin\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2})j)\\ \space\\ =(\cos\frac{\theta_{yaw}}{2}\cos\frac{\theta_{pitch}}{2}\cos\frac{\theta_{roll}}{2}+\sin\frac{\theta_{yaw}}{2}\sin\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2}, \space\\ \cos\frac{\theta_{yaw}}{2}(\cos\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2}k+\cos\frac{\theta_{roll}}{2}\sin\frac{\theta_{pitch}}{2}i-(\sin\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2})j)+\cos\frac{\theta_{pitch}}{2}\cos\frac{\theta_{roll}}{2}(\sin\frac{\theta_{yaw}}{2}j)+(\sin\frac{\theta_{yaw}}{2}\cos\frac{\theta_{pitch}}{2}\sin\frac{\theta_{roll}}{2})i-(\sin\frac{\theta_{yaw}}{2}\cos\frac{\theta_{roll}}{2}\sin\frac{\theta_{pitch}}{2})k) q y a w ⋅ q p i t c h ⋅ q ro ll = ( cos 2 θ y a w , sin 2 θ y a w j ) ⋅ ( cos 2 θ p i t c h , sin 2 θ p i t c h i ) ⋅ ( cos 2 θ ro ll , sin 2 θ ro ll k ) = ( cos 2 θ y a w , sin 2 θ y a w j ) ⋅ ( cos 2 θ p i t c h cos 2 θ ro ll , cos 2 θ p i t c h sin 2 θ ro ll k + cos 2 θ ro ll sin 2 θ p i t c h i − ( sin 2 θ p i t c h sin 2 θ ro ll ) j ) = ( cos 2 θ y a w cos 2 θ p i t c h cos 2 θ ro ll + sin 2 θ y a w sin 2 θ p i t c h sin 2 θ ro ll , cos 2 θ y a w ( cos 2 θ p i t c h sin 2 θ ro ll k + cos 2 θ ro ll sin 2 θ p i t c h i − ( sin 2 θ p i t c h sin 2 θ ro ll ) j ) + cos 2 θ p i t c h cos 2 θ ro ll ( sin 2 θ y a w j ) + ( sin 2 θ y a w cos 2 θ p i t c h sin 2 θ ro ll ) i − ( sin 2 θ y a w cos 2 θ ro ll sin 2 θ p i t c h ) k ) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static Quaternion ToQ ( float yaw , float pitch , float roll )
{
yaw *= Mathf . Deg2Rad ;
pitch *= Mathf . Deg2Rad ;
roll *= Mathf . Deg2Rad ;
float rollOver2 = roll * 0.5f ;
float sinRollOver2 = ( float ) Math . Sin (( double ) rollOver2 );
float cosRollOver2 = ( float ) Math . Cos (( double ) rollOver2 );
float pitchOver2 = pitch * 0.5f ;
float sinPitchOver2 = ( float ) Math . Sin (( double ) pitchOver2 );
float cosPitchOver2 = ( float ) Math . Cos (( double ) pitchOver2 );
float yawOver2 = yaw * 0.5f ;
float sinYawOver2 = ( float ) Math . Sin (( double ) yawOver2 );
float cosYawOver2 = ( float ) Math . Cos (( double ) yawOver2 );
Quaternion result ;
result . w = cosYawOver2 * cosPitchOver2 * cosRollOver2 + sinYawOver2 * sinPitchOver2 * sinRollOver2 ;
result . x = cosYawOver2 * sinPitchOver2 * cosRollOver2 + sinYawOver2 * cosPitchOver2 * sinRollOver2 ;
result . y = sinYawOver2 * cosPitchOver2 * cosRollOver2 - cosYawOver2 * sinPitchOver2 * sinRollOver2 ;
result . z = cosYawOver2 * cosPitchOver2 * sinRollOver2 - sinYawOver2 * sinPitchOver2 * cosRollOver2 ;
return result ;
}
회전 행렬에서 사원수 회전행렬에서 사원수는 대게(opilio crab) 외적을 사용하게 되는데,
이 외적 정보는 이미 행렬에 모두 포함되어 있습니다.
(대게는 농담입니다. 이거 하고 있으면 진짜 제정신이 아니예요)
대각 행렬(Trace,Tr)의 활용
대각 행렬의 합
t + 1 = 4 w 2 r = t + 1 = 2 w w = r 2 t+1=4w^2\\ r=\sqrt{t+1}=2w\\ w=\frac{r}{2} t + 1 = 4 w 2 r = t + 1 = 2 w w = 2 r 대각 행렬을 구해 w w w
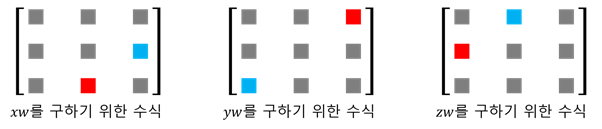
x w = m [ 1 ] [ 2 ] − m [ 2 ] [ 1 ] y w = m [ 2 ] [ 0 ] − m [ 0 ] [ 2 ] z w = m [ 0 ] [ 1 ] − m [ 1 ] [ 0 ] xw=m[1][2]-m[2][1]\\ yw=m[2][0]-m[0][2]\\ zw=m[0][1]-m[1][0] x w = m [ 1 ] [ 2 ] − m [ 2 ] [ 1 ] y w = m [ 2 ] [ 0 ] − m [ 0 ] [ 2 ] z w = m [ 0 ] [ 1 ] − m [ 1 ] [ 0 ] 예외 상황 : 트레이스 값이 1보다 작거나 같으면 해가 존재하지 않음.
따라서 다른 요소부터 구해야 하는 상황 발생
켄 슈메이크(Ken Shoemake)의 알고리즘.
트레이스 값이 0보다 크면 첫 번째 방식을 적용해 해결 트레이스 값이 0보다 작으면 다른 로직을 적용한다.x , y , z x,y,z x , y , z 다른 요소를 조합해 가장 큰 값을 먼저 계산한다. 나머지 두 요소는 아래 식으로부터 계산한다. 세 요소 값을 모두 구했다면 w w w
회전 행렬에서 사원수로 변환하는 방법 구현한 코드를 분석하시오. 행기반 행렬 - 언리얼 엔진의 변환 코드 ( 회전 행렬 → 사원수 ) 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
inline FQuat :: FQuat ( const FMatrix & M )
{
// If Matrix is NULL, return Identity quaternion. If any of them is 0, you won't be able to construct rotation
// if you have two plane at least, we can reconstruct the frame using cross product, but that's a bit expensive op to do here
// for now, if you convert to matrix from 0 scale and convert back, you'll lose rotation. Don't do that.
if ( M . GetScaledAxis ( EAxis :: X ). IsNearlyZero () \ vert \ vert M . GetScaledAxis ( EAxis :: Y ). IsNearlyZero () \ vert \ vert M . GetScaledAxis ( EAxis :: Z ). IsNearlyZero ())
{
* this = FQuat :: Identity ;
return ;
}
#if !(UE_BUILD_SHIPPING \vert \vert UE_BUILD_TEST)
// Make sure the Rotation part of the Matrix is unit length.
// Changed to this (same as RemoveScaling) from RotDeterminant as using two different ways of checking unit length matrix caused inconsistency.
if ( ! ensure (( FMath :: Abs ( 1. f - M . GetScaledAxis ( EAxis :: X ). SizeSquared ()) <= KINDA_SMALL_NUMBER ) && ( FMath :: Abs ( 1. f - M . GetScaledAxis ( EAxis :: Y ). SizeSquared ()) <= KINDA_SMALL_NUMBER ) && ( FMath :: Abs ( 1. f - M . GetScaledAxis ( EAxis :: Z ). SizeSquared ()) <= KINDA_SMALL_NUMBER )))
{
* this = FQuat :: Identity ;
return ;
}
#endif
//const MeReal *const t = (MeReal *) tm;
float s ;
// Check diagonal (trace)
const float tr = M . M [ 0 ][ 0 ] + M . M [ 1 ][ 1 ] + M . M [ 2 ][ 2 ];
if ( tr > 0.0 f )
{
float InvS = FMath :: InvSqrt ( tr + 1. f );
this -> W = 0.5 f * ( 1. f / InvS );
s = 0.5 f * InvS ;
this -> X = ( M . M [ 1 ][ 2 ] - M . M [ 2 ][ 1 ]) * s ;
this -> Y = ( M . M [ 2 ][ 0 ] - M . M [ 0 ][ 2 ]) * s ;
this -> Z = ( M . M [ 0 ][ 1 ] - M . M [ 1 ][ 0 ]) * s ;
}
else
{
// diagonal is negative
int32 i = 0 ;
if ( M . M [ 1 ][ 1 ] > M . M [ 0 ][ 0 ])
i = 1 ;
if ( M . M [ 2 ][ 2 ] > M . M [ i ][ i ])
i = 2 ;
static const int32 nxt [ 3 ] = { 1 , 2 , 0 };
const int32 j = nxt [ i ];
const int32 k = nxt [ j ];
s = M . M [ i ][ i ] - M . M [ j ][ j ] - M . M [ k ][ k ] + 1.0 f ;
float InvS = FMath :: InvSqrt ( s );
float qt [ 4 ];
qt [ i ] = 0.5 f * ( 1. f / InvS );
s = 0.5 f * InvS ;
qt [ 3 ] = ( M . M [ j ][ k ] - M . M [ k ][ j ]) * s ;
qt [ j ] = ( M . M [ i ][ j ] + M . M [ j ][ i ]) * s ;
qt [ k ] = ( M . M [ i ][ k ] + M . M [ k ][ i ]) * s ;
this -> X = qt [ 0 ];
this -> Y = qt [ 1 ];
this -> Z = qt [ 2 ];
this -> W = qt [ 3 ];
DiagnosticCheckNaN ();
}
}
분석 [ 1 − 2 ( y ′ 2 + z ′ 2 ) 2 ( x ′ y ′ − w z ′ ) 2 ( x ′ z ′ + w y ′ ) 0 2 ( x ′ y ′ + w z ′ ) 1 − 2 ( x ′ 2 + z ′ 2 ) 2 ( y ′ z ′ − w x ′ ) 0 2 ( x ′ z ′ − w y ′ ) 2 ( y ′ z ′ + w x ′ ) 1 − 2 ( x ′ 2 + y ′ 2 ) 0 0 0 0 1 ] \left[\begin{matrix} 1-2(y'^2+z'^2)&2(x'y'-wz')&2(x'z'+wy')&0\\ 2(x'y'+wz')&1-2(x'^2+z'^2)&2(y'z'-wx')&0\\ 2(x'z'-wy')&2(y'z'+wx')&1-2(x'^2+y'^2)&0\\ 0&0&0&1 \\\end{matrix}\right] 1 − 2 ( y ′2 + z ′2 ) 2 ( x ′ y ′ + w z ′ ) 2 ( x ′ z ′ − w y ′ ) 0 2 ( x ′ y ′ − w z ′ ) 1 − 2 ( x ′2 + z ′2 ) 2 ( y ′ z ′ + w x ′ ) 0 2 ( x ′ z ′ + w y ′ ) 2 ( y ′ z ′ − w x ′ ) 1 − 2 ( x ′2 + y ′2 ) 0 0 0 0 1 여기서부터 시작을 합시다.
q x 2 + q y 2 + q z 2 + q w 2 = 1 q w 2 = 1 − q x 2 − q y 2 − q z 2 qx^2+qy^2+qz^2+qw^2 = 1 \\ qw^2 = 1 - qx^2-qy^2-qz^2 q x 2 + q y 2 + q z 2 + q w 2 = 1 q w 2 = 1 − q x 2 − q y 2 − q z 2 양변에 4를 곱해
4 q w 2 = 4 − 4 q x 2 − 4 q y 2 − 4 q z 2 4 q w 2 = 1 + ( 1 − 2 q y 2 − 2 q z 2 ) + ( 1 − 2 q x 2 − 2 q z 2 ) + ( 1 − 2 q x 2 − 2 q y 2 ) 4qw^2 = 4 - 4qx^2 - 4qy^2 - 4qz^2\\ 4qw^2 =1 +(1-2qy^2-2qz^2)+(1-2qx^2-2qz^2)+(1-2qx^2-2qy^2) 4 q w 2 = 4 − 4 q x 2 − 4 q y 2 − 4 q z 2 4 q w 2 = 1 + ( 1 − 2 q y 2 − 2 q z 2 ) + ( 1 − 2 q x 2 − 2 q z 2 ) + ( 1 − 2 q x 2 − 2 q y 2 ) 이를 이제 위의 행렬에서 가져온다면,
4 q w 2 = 1 + ( m 00 ) + ( m 11 ) + ( m 22 ) 4qw^2 =1 +(m_{00})+(m_{11})+(m_{22}) 4 q w 2 = 1 + ( m 00 ) + ( m 11 ) + ( m 22 ) 이때 이 값은 대각행렬의 값으로 (트레이스의 값으로) 알려져있으므로
q w = s q r t ( 1 + T r ) 2 qw=\frac{ sqrt(1+Tr)}{2} qw = 2 s q r t ( 1 + T r ) 다만 이때는 양수일때만 사용할 수 있습니다.
그에 따라 코드에서는 대각행렬의 값이 음수인지 양수인지를 판단하여,
2 ( q y q z − q x q w ) − 2 ( q y q z + q x q w ) = q x 2 ( y ′ z ′ − w x ′ ) − 2 ( y ′ z ′ + w x ′ ) = q x ( m 21 ) − ( m 12 ) = q x \begin{align*} 2(qyqz - qxqw) - 2(qyqz + qxqw)=qx\\ 2(y'z'-wx')-2(y'z'+wx')=qx\\ (m_{21})-(m_{12})=qx \end{align*} 2 ( q y q z − q x qw ) − 2 ( q y q z + q x qw ) = q x 2 ( y ′ z ′ − w x ′ ) − 2 ( y ′ z ′ + w x ′ ) = q x ( m 21 ) − ( m 12 ) = q x 이런식으로 구하는 것 같습니다.
하지만 이제 대각행렬이 음수일때, 제일 큰 값을 찾아, 쉬프트하여 찾습니다.
쿼터니언을 시각화 하였을 때, 한쪽이 밀리면 다른쪽이 밀려들어가듯, 행렬에서도 외적이 적용된 부분이 기준점에 따라 다르게 해석할 수 있음을 사용한 아주 똑똑한 방법이죠.
맺음말