Home 11. Local Space, Texture Mapping, Bilinear Interpolation
Post
Cancel

11. Local Space, Texture Mapping, Bilinear Interpolation

Posted May 17, 2021
By Jung Jisang
36 min read

Local Space, Texture Mapping, Bilinear Interpolation

텍스쳐 매핑 (Texture Mapping)

픽셀과 텍셀

픽셀과 텍셀. 결국 점이기 때문에

벡터 - 아핀공간의 점 - 픽셀 - 텍셀 을 전체적으로 인지하는 것이 좋을 것 같습니다.

앞의 두개는 이미 했으므로, 픽셀과 텍셀에 대해 나타내자면…

아니 픽셀도 이미 레스터라이즈 단계에서설명한 적 있습니다.

저희는 모니터의 화면을 구성하는 화소, 즉 픽셀을 기준으로 다루겠습니다.

벡터공간에서는 어느 방향을 가르키는 벡터가 존재하고,

아핀공간은 이를 확장하여 어느 지점에 존재하는 점이 존재하며,

화면의 단위는 픽셀이라는 물리적인 점으로 존재합니다.

그리고 텍스쳐에게는 텍셀이라는 단위를 사용하는 좌표계가 존재합니다.

그리고 이걸, 가로 세로의 범위가 1인 좌표, UVUV 좌표라고 말합니다.

텍셀로부터 텍스쳐의 색상을 얻기위한 방법

그렇다면 텍스쳐의 색상을 얻기 위해서는 어떻게 해야 할까요?

픽셀을 사용하는 화면좌표계에서 텍셀을 사용하는 텍스쳐좌표계로 변환된 좌표의 값을 읽어들이는것이 타당하다고 생각합니다.

아핀좌표계에서 점을 벡터로 바꾸는것과 같이 결국 변환을 하는 것입니다.

결론적으로 리매핑입니다.

1
2
3
4
5
6

public static float Remap(
				this float value, 
				in (float, float) input, 
				in (float, float) output)
 => output.Item1 + (output.Item2 - output.Item1) * 
((value - input.Item1) / (input.Item2 - input.Item1));

제가 즐겨쓰는 리매핑 확장함수입니다. (자주써서 한번쯤 소개해보고 싶었습니다)

그렇게 삼각형에 꽉 맞게 채색해야하기 때문에,

삼각형 내부에 존재하는 0에서 1의 범위를 갖는 좋은 좌표계인 무게중심좌표계를 사용합니다.

앗, 닭이 먼저인지 달걀이 먼저인지는… 무게중심좌표계가 먼저가 아닐까 싶습니다.

시각적으로 보자면 삼각형의 픽셀에 해당하는 지점의 삼각형의 무게중심 좌표계를 통해 텍스처의 UV좌표계에 해당하는 텍셀을 읽어들여 그리는게 될 것 같습니다.

하지만 여기서 문제가 있습니다.

텍셀이 픽셀보다 큰 경우가 문제가 생기는데 어떻게 해결할 것인지 결정해야합니다.

첫번째로 아주 단순한,

  • 가장 가까운 픽셀을가져옴 (Nearest-neighbor interpolation)

게임에서는 None, off 혹은 근접점 필터링, Point 등으로 불립니다.

정말 UV좌표에서 가장 가까운 텍셀을 색칠하는 방법입니다.

도트느낌을 내거나, 깔끔하게 나뉘는 그림을 보고싶다면 이렇게 처리합니다.

두번째로 단순하진 않은

  • 둘러싼 네개의 색상값을 불러와서 보간 (Bi-linear-interpolation)

게임에서는 흔히 쌍선형 필터링이라는 항목으로 확인할 수 있습니다.

가까운 좌하단, 우하단, 좌상단, 우상단의 네 텍셀을 불러와 무게중심에 따라 보간합니다.

…그리고 그렇다면 삼선형 필터링을 놔둘순 없죠!

  • 둘러싼 여덟개의 색상값을 불러와 보간 ?! (trilinear-interpolation)

하지만 속으면 안됩니다. 인접한 대각선의 텍셀까지 불러오는게 아닙니다!

그러면 어떻게 여덟개의 텍셀을 보간하는걸까요?

그건 불러오는 구조의 차원을 보아야합니다

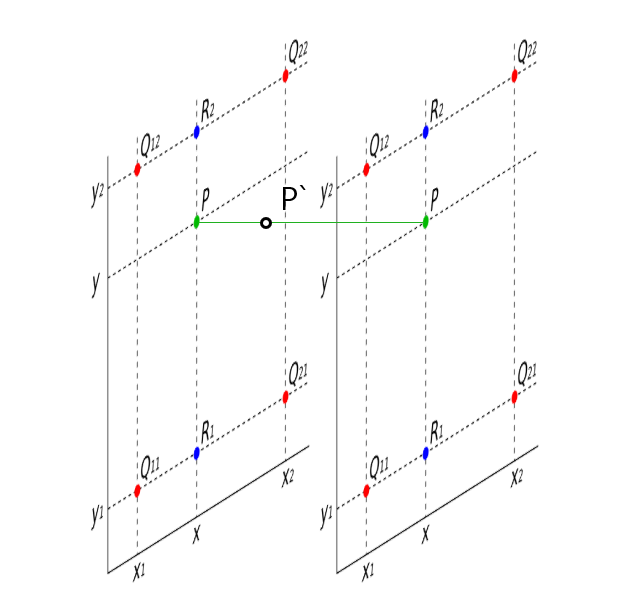
Untitled%205.png

이를 이해하기 위해서는 밉맵의 구조에 대해 알아야하는데,

단순하게 말하면 거리에 따라 낭비를 줄이기 위해 미리 만들어둔 저해상도의 텍스처를 사용하는것입니다.

즉 카메라와의 거리에 따라 두장의 텍스처 사이에 존재하게 되는데,

이때 삼선형의 경우 가까운 텍스처의 쌍선형, 먼 텍스쳐의 쌍선형의 두 값을 거리에 따라 보간한 색상을 사용하게 됩니다.

정면에서 바라본 마인크래프트의 캐릭터 구현

..그림판에 네모들을 그린 다음, 각 점에 마우스를 올려 좌측하단에 적히는 좌표를 외우고, 전체 캔버스 크기의 절반을 뺀 값을 암기한 다음 버텍스 정의 코드를 클릭해 외워뒀던 숫자들을 하나하나 적다가.. 글만봐도 귀찮은 이 일을 대략 20% 완료하였을때 어짜피 사각형 몇갠데 그냥 코드로 생성해서 처리하자 싶어서 구현했습니다.

유니티에서 UI를 사용하여 빈 사각형 이미지를 만듭니다.

일단 스티브가 어떻게 생겼는지 기억이 안나니 대충 배치해줍니다.

언제봐도 정겨운 유니티 샘플 씬

언제봐도 정겨운 유니티 샘플 씬

어디보자 원본 프로젝트 코드에는 어떻게 넣어야할까요?

1

Vertex2D(Vector2(/* X */, /* Y */), LinearColor(), Vector2(0.125f, 0.875f)),

아주 좋습니다.

마치 복붙을 하기위해 만들어진 구조입니다.

결국 저희는 저 첫 벡터만 긁어오면 되니

포맷을 다음과 같이 만든 후 , 유니티 코드를 작성합니다.

UV는 어짜피 나중에 직접 텍스쳐보고 넣어야 하니 포맷에 적지 않습니다.

복사-붙여넣기 하는데 방해만 됩니다.

(보통은 UV를 보고 텍스쳐를 그려야하지만… 이것이 리버스 엔지니어링?)

그러면 포맷이 다음과 같이 나옵니다.

1

private const string format = "Vertex2D(Vector2({0}, {1}), LinearColor(),  ";

코드로 작성해봅시다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

[ExecuteInEditMode]
public class TempGetVertexPos : MonoBehaviour
{

    [SerializeField]
    private List<Image> images;

    private List<Vector2> vtx = new List<Vector2>();

    private const string format = "Vertex2D(Vector2({0}, {1}), LinearColor(),  ";

    private void OnEnable()
    {
        vtx.Clear();

        foreach (var image in images)
        {
            var rect = image.rectTransform.rect;

            vtx.Add((image.transform.TransformPoint(new Vector2(rect.xMin, rect.yMin)) - new Vector3(Screen.width, Screen.height, 0) * 0.5f) * 0.5f);
            vtx.Add((image.transform.TransformPoint(new Vector2(rect.xMin, rect.yMax)) - new Vector3(Screen.width, Screen.height, 0) * 0.5f) * 0.5f);
            vtx.Add((image.transform.TransformPoint(new Vector2(rect.xMax, rect.yMax)) - new Vector3(Screen.width, Screen.height, 0) * 0.5f) * 0.5f);
            vtx.Add((image.transform.TransformPoint(new Vector2(rect.xMax, rect.yMin)) - new Vector3(Screen.width, Screen.height, 0) * 0.5f) * 0.5f);
        }

        var list = vtx.Select((vec) => { return string.Format(format, vec.x.ToString("F2") + "f", vec.y.ToString("F2") + "f"); });

        Debug.Log("v : " + string.Join("\n", list.ToArray()));
    }
}
  1. 각 사각형 이미지들의 각 점의 위치를 알기 위해 rect를 받아와, 4개의 점을 찾아줍니다.
    1. 이때 삼각형을 그리는 순서는 0 1 2 0 2 3, 즉 좌하단 - 좌상단 - 우상단 - 우하단 입니다.
  2. 저 점들의 위치 값은 로컬좌표이기때문에 월드좌표로 변환하기위해 transformPoint 처리를 해줍니다. 그러면 화면좌표계가 나옵니다.
  3. 실제 사용할 좌표계인 중앙으로 이동시키기 위해 화면의 절반만큼을 빼줍니다
  4. 화면이 19201080이기때문에 대강 800600에 맞추기 위해 최종 좌표를 반토막 내줍니다.
  5. 너무 길면 눈치보이니까(?) 적당히 잘라서 string화 해준 다음, 로그로 찍어줍니다.

그러면 이제 OnEnable시 로그가 찍힙니다

12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%201.png

로그를 긁어서 vs에 넣어줍니다.

UV를 일단 머리값으로 다 복사해서 만 넣어준 다음,

렌더링하게되면 다음과 같이나옵니다.

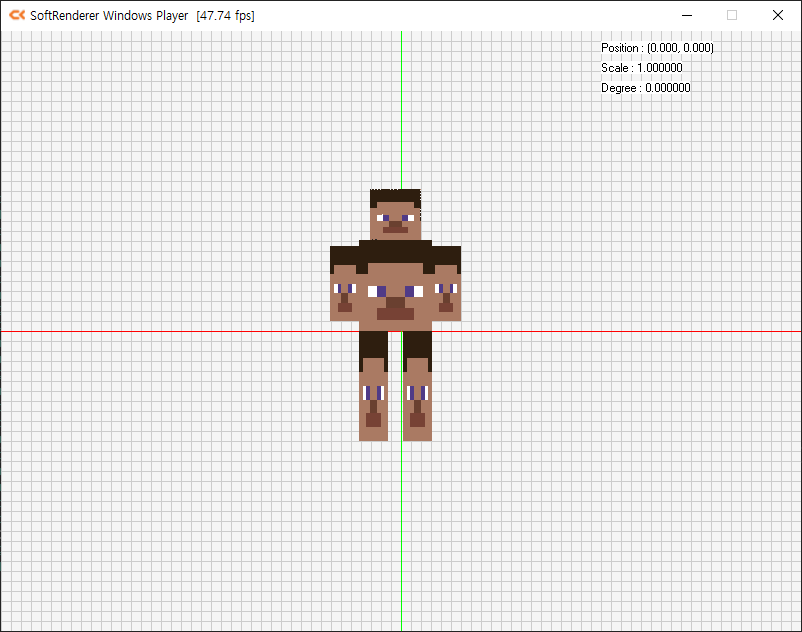
12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%202.png

이제 uv맵핑만 하면됩니다.

물론 이것도 노가다입니다.

자동화를 할만한 식이 안떠오르면…. 직접 손수 적어야죠.

(그리고 이 노가다는 결국 잘못 적혔다고 합니다. 참조)

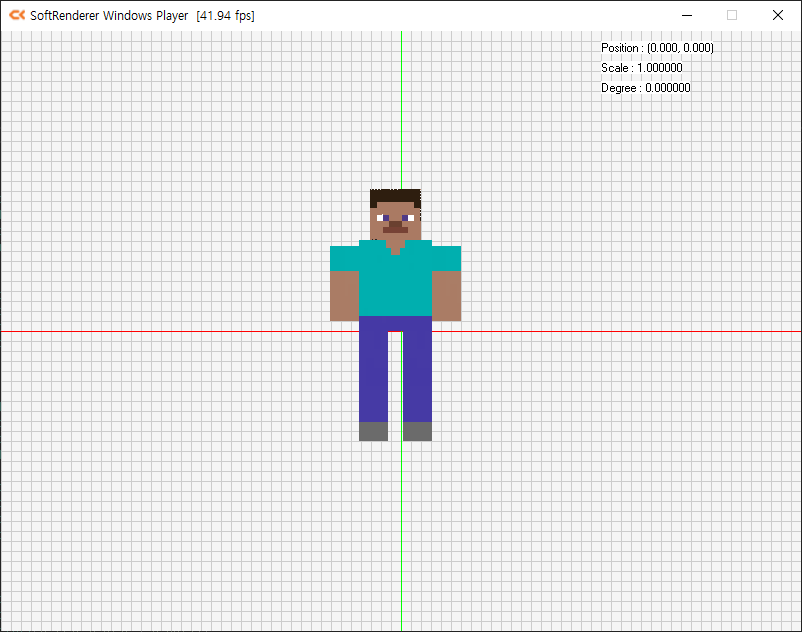
12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%203.png

아이 죽겠다 ㅎㅎ

뭔가 어깨뽕이 있는 길쭉길쭉한 다리를 가진 미남이 나왔는데…

그래서 스티브는 원래 어떻게 생겼었죠? 잘 모르겠습니다.

게임엔진의 구조

로컬공간과 월드공간의 개념 및 여러개의 공간이 필요한 이유

물체 하나에도 여러개의 정점이 있습니다.

그리고 각 정점은 당연하게도 위치정보를 가지고 있겠죠.

그리고 물체가 바라보는 방향, 물체가 있는 위치, 물체의 크기 등의 정보도 있을것입니다.

정점기준에서는 정점이 존재하는 세상은 ‘물체’가 바라보는 방향, 위치, 크기에 따라 달라지게 됩니다. 물체 기준으로 좌표계가 설정 되는 것입니다.

그리고 물체 역시 생각해본다면, 자동차에 속해있는 물체 목록중 창문이 있다고 가정한다면,

이 창문 역시 자동차의 위치, 방향,크기에 종속적으로 존재해야합니다.

차량이 이동하는데 창문은 여전히 원위치에 덩그라니 있다면 안되는것이니까요.

이에 따라 각 물체만의 고유한 공간이라는 개념이 존재하게 됩니다.

해당 물체에 의존된 물체역시 존재할 수 있으며, 물체 자신의 버텍스도 물체의 공간에 존재하게 되는것이죠. 이를 로컬공간이라고 합니다.

아까 설명한 자동차를 로컬공간을 생각한 계층적으로 접근해 본다면

  • 자동차
    • 프레임
      • 외골격
        • 창문
      • 엔진
        • 기어
      • 휠
        • 고무

처럼 나타낼 수 있을 것입니다.

그리고 각 물체는 자신의 상위객체에 종속적이죠.

만약 그렇다면 타이어 고무의 버텍스 위치정보를 화면에 얻기 위해서는

타이어 고무의 버텍스를 고무 행렬에 곱하고, 해당값을 휠의 행렬에 곱하고, 프레임의 행렬에 곱하고, 자동차의 행렬에 곱하고….. 이렇게 처리되어야합니다.

그렇게 최종적으로 나오는 것은 처음 세상을 설정한 사람이 설정한 원점, 축 방향, 임의의 크기를 가진 하나의 물체의 로컬좌표계입니다. 하지만 이걸 사용자는 수정할 수 없습니다.

이 물체의 공간을 월드공간이라고 합니다.

모든 물체는 어떤 수정불가능한 ‘설정한’ 물체의 로컬공간 위에서 존재한다고 보는 것입니다.

마치 아핀공간의 원점같은 느낌이죠.

아무튼 이렇게 여러 로컬공간을 가진 물체들을 알아서 처리하고,

마지막에 변환을 통해 뽑아낼 수 있게 합니다.

그리고 그걸 담당하는 좋은 데이터집합이 있죠.

트랜스폼(Transform)

직역하자면 변환입니다.

엔진에서 사용되는 좌표 변환을 위한 데이터의 집합입니다.

총체적인 좌표변환을 위한 값들을 감싼 하나의 구조이며,

크기, 회전, 변위에 대한 값이 있습니다.

각각이 행렬로 처리될 수 있으며,

이 행렬을 미리 곱해둠으로써 하나의 변환으로 만들 수 있습니다.

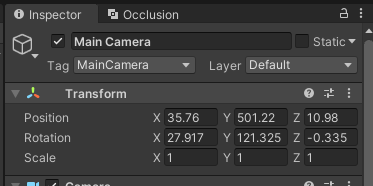
12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%204.png

유니티에서는 주로 다음과 같이 표현됩니다.

다음과 같이 오브젝트의 부모객체의 로컬 좌표계에 존재하는 객체의 좌표,회전,크기 값을 노출합니다.

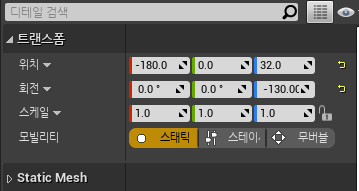
언리얼에서는 다음과 같이 표현됩니다.

언리얼과 안 친해서 로컬기준인지 월드기준인지는 잘 모르겠습니다.

12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%205.png

유니티 트랜스폼을 뜯어봅시다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

//in Runtime/Transform/ScriptBindings/TransformScriptBindings

// Matrix that transforms a point from world space into local space (RO).
public extern Matrix4x4 worldToLocalMatrix { get; }
// Matrix that transforms a point from local space into world space (RO).
public extern Matrix4x4 localToWorldMatrix { get; }

// Moves the transform in the direction and distance of /translation/.
public void Translate(Vector3 translation, [UnityEngine.Internal.DefaultValue("Space.Self")] Space relativeTo)
{
    if (relativeTo == Space.World)
        position += translation;
    else
        position += TransformDirection(translation);
}

[NativeMethod("RotateAround")]
internal extern void RotateAroundInternal(Vector3 axis, float angle);

// Rotates the transform around /axis/ by /angle/ degrees.
public void Rotate(Vector3 axis, float angle, [UnityEngine.Internal.DefaultValue("Space.Self")] Space relativeTo)
{
    if (relativeTo == Space.Self)
        RotateAroundInternal(transform.TransformDirection(axis), angle * Mathf.Deg2Rad);
    else
        RotateAroundInternal(axis, angle * Mathf.Deg2Rad);
}

// Transforms /vector/ from local space to world space.
public extern Vector3 TransformVector(Vector3 vector);

// Transforms vector /x/, /y/, /z/ from local space to world space.
public Vector3 TransformVector(float x, float y, float z) { return TransformVector(new Vector3(x, y, z)); }

// Transforms a /vector/ from world space to local space. The opposite of Transform.TransformVector.
public extern Vector3 InverseTransformVector(Vector3 vector);

// Transforms the vector /x/, /y/, /z/ from world space to local space. The opposite of Transform.TransformVector.
public Vector3 InverseTransformVector(float x, float y, float z) { return InverseTransformVector(new Vector3(x, y, z)); }

이동과 회전, 크기에 대한 조작 및 최종 행렬, 역행렬들을 제공하며,

또한 좌표변환을 위한 코드를 제공합니다.

정리하자면 트랜스폼의 역할은 변환을 위한 3가지 데이터에 대한

총괄적인 데이터 집합 및 연산도움을 처리합니다.

(Wrapper? 뭐라고 해야할 지 모르겟습니다)

트랜스폼을 구현할 때의 행렬은 왜 TRS를 사용하는가?

과거에 TRSvTRSv 를 설명하며 왜 그렇게 되는지 적었던 적 있습니다.

6주차 - 크기행렬과 회전행렬중 어떤것을 우선해야하는가

예를 들어

하나의 물체를 생각해 봅시다.

  • 45도 돌아간 사각형
  • 좌우가 상하에 비해 2배 김
  • 오른쪽로 N만큼 이동

만약 스케일을 하기 전에 회전을 한다면, 옆으로 늘어난 마름모같은 모양이 될 것이고,

이는 아마 저희가 생각하는 결과물과 다를 것 입니다.

또한 회전하기전에 이동을 하여 물체의 중심이아닌 물체의 아래 기준으로 회전한듯한 모양역시

저희가 생각하는 결과물과는 다른 형태입니다.

예제프로그램을 돌려봤습니다

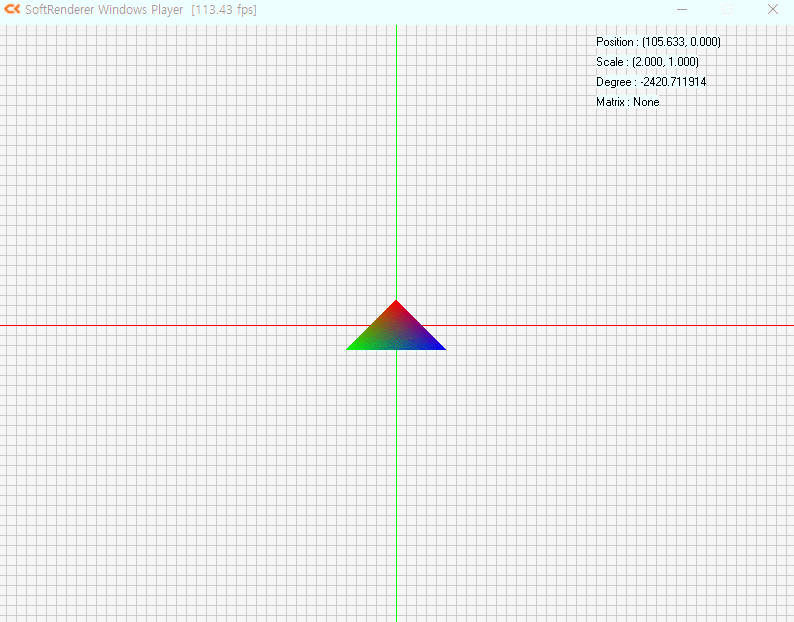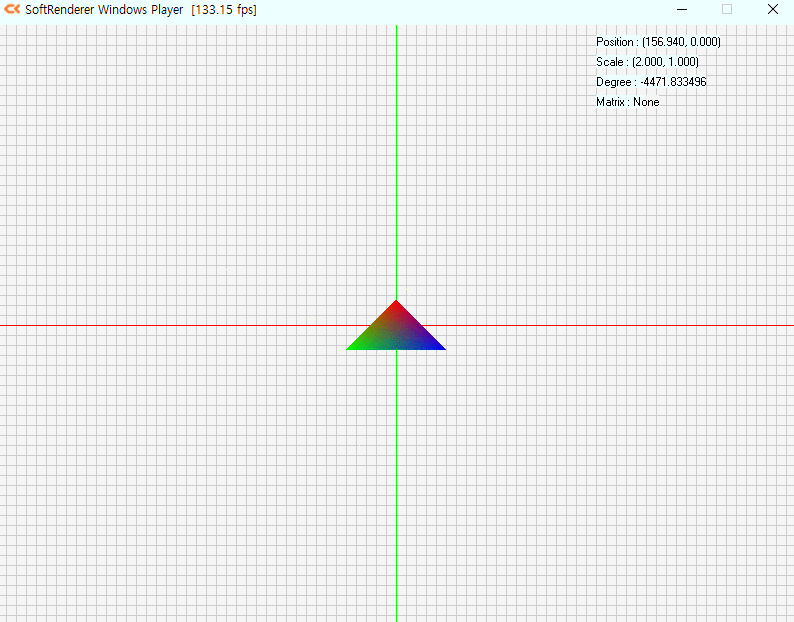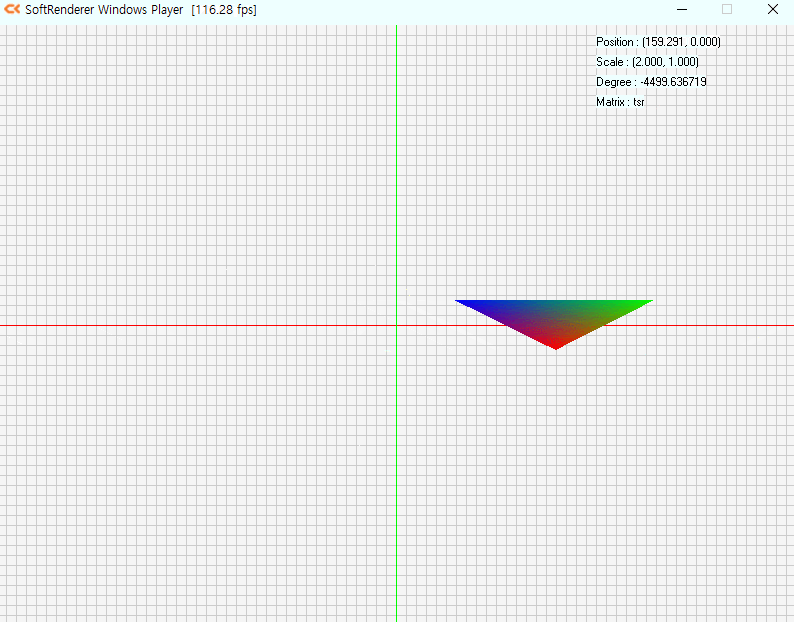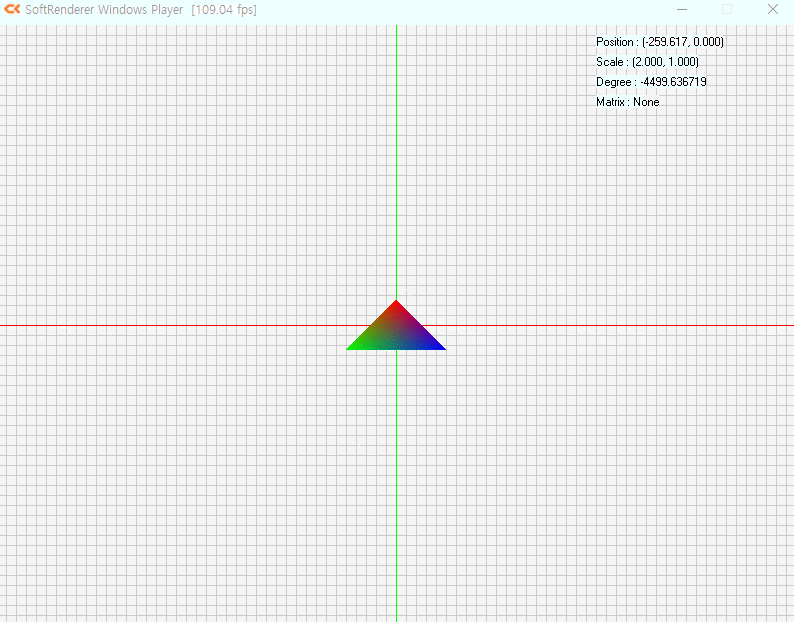
12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/assignment_GIF_12_1.gif

행렬곱에따라 모든것이 바뀌는걸 볼 수 있습니다.

결론적으로 직관적으로 생각할 때

크기는 회전에 영향을 받으며,

회전은 이동에 영향을 받기 때문에

영향을 받지 않는 순서인

(영향을 끼치지 않는 순서인)

크기 - 회전 - 이동 순서로 진행을 하게 됩니다.

최종생성되는 모델링행렬을 직접 유도

드디어 끝을 향해 가는 기분이네요.

이때까지 정리한걸 대 방출할 기회입니다.

크기행렬

따라서 기본 행렬은 다음과 같습니다. x축의 크기인 xscalex_{scale} 과 y축의 크기인 yscaley_{scale} 로 표기하였습니다. [xscale00yscale]\begin{bmatrix} x_{scale} & 0\\ 0 & y_{scale} \end{bmatrix}

회전행렬

따라서 임의의 각 쎄타에 대한 회전행렬은 [cos(θ)−sin(θ)sin(θ)cos(θ)]\begin{bmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{bmatrix}

이동행렬

다시 이걸 행렬로 바꾸게 된다면,

$$ \bold A\vec v =\begin{bmatrix} 1 & 0 & e
0 & 1 & f
0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x
y
1 \end{bmatrix} =

\begin{bmatrix} 1 \cdot x + 0 \cdot y + e \cdot 1
0 \cdot x + 1 \cdot y + f \cdot 1
0 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 \end{bmatrix} =

\begin{bmatrix} x+e
y+f
1 \end{bmatrix} =

\bold u $$

따라서 다시 정리한다면

S(scale)=[sx000sy0001]R(rotation)=[cosθ−sinθ0sinθcosθ0001]T(translation)=[10tx01ty001]S_{(scale)}= \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ R_{(rotation)}= \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\\ T_{(translation)}= \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}\\

양식미를 위한 행렬곱을 첨가하고,

행렬의 곱셈

행렬의 곱셈

과제에서는 적지 않았지만 『행렬의 곱은 내적』이다 를 상기하며

벡터의 내적

벡터의 내적

마무리를 지어줍시다.

M=TRS=[cosθ⋅sx−sinθ⋅sytxsinθ⋅sxcosθ⋅syty001]M=TRS= \begin{bmatrix} cos\theta\cdot s_x & -sin\theta\cdot s_y & t_x \\ sin\theta\cdot s_x & cos\theta\cdot s_y & t_y \\ 0 & 0 & 1 \end{bmatrix}\\

마치 하나하나 쌓아온 무언가들이 폭발하는 것 같습니다.

기분 좋네요

게임로직과 렌더링로직이 하는 역할 정리

게임로직에서는 굳이 행렬을 사용하여 변환할일이 많지 않습니다.

이동은 단순하게 스칼라곱 및 벡터의 덧셈으로 처리 되며,

회전은 오일러변환을 통한 벡터의 합,

특정 벡터의 회전은 오일러 - 쿼터니언을 통한 쿼터니언과 벡터의 곱셈으로,

스케일역시 단순하게 스칼라곱과 벡터의 덧셈으로 처리가 됩니다.

게임로직 : 변환 연산을 처리하며, 처리된 각각의 트랜스폼 정보를 해당 타이밍에 확정합니다.

렌더링 로직 : 로컬공간의 메시에 있는 각 버텍스들을 로컬 To 화면 행렬로 변환하여 최종적으로 화면위치에 삼각형을 뿌리게 됩니다.

Bilinear Interpolation 구현

음… 위에서 한번 봤었죠?

일단 특정 값에 대해 인접한 4 픽셀을 긁으면 된다는 것 까지는 인지하였습니다.

초기 프로젝트는 분명 Nearest-neighbor interpolation 으로 구현되었다고 믿고 진행합니다.

하지만 코드는 Floor To Int를 진행하고 있었습니다.

생각상으론 Round가 더 적절하다고 느꼈는데, Floor를 처리하고 있으니…

아마 -0.5 처리를 겸하기 위해 Round가 아닌 Floor을 사용하는가? 싶습니다.

그러면서 softRenderer의 Rasterization Rules과 연관이 있는게 아닌가? 하는 생각이 들자

좌표계가 혼란스러워지기 시작했습니다.

일단 구현을 보면서… 중앙기준 0.5 범위의 영역을 얻고 싶은데, FloorToInt로 구현되어 있기 때문에 전체적으로 0.5를 빼줍니다. 그리고 해당값의 다음값을 가져온다면, 두 점을 제대로 가져올 수 있겠죠.

그리고 무게중심 좌표계는 간단히 원래값 - 처리된 값 을 통해 0~1 사이의 ‘버려진 값’을 가져올 수 있습니다. 여기서는 Fmod를 사용하여 구현하였습니다.

저희가 가져올 대상은 분명합니다. Floor를 F, Floor + 1 을 C라고 하겠습니다

기존에는 FF를 가져왔다면, FF, CC, FC, CF를 가져와 그리면 될 것 입니다.

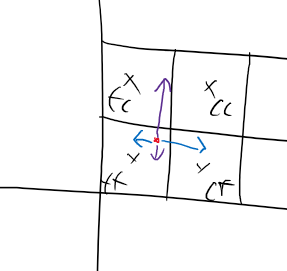
- 실제 보면서 작업한 그림 - 좌표계만 통일된다면 개념은 동일하므로, 생각을 위한 좌표계는 데카르트 좌표계를 사용하였습니다.

  • 실제 보면서 작업한 그림 - 좌표계만 통일된다면 개념은 동일하므로, 생각을 위한 좌표계는 데카르트 좌표계를 사용하였습니다.

이제 생각난 문제는 edgeCase… 만약 네 점중 존재하지 않는 점이 있는 경우입니다.

이를 위해 한번 검사를 진행합니다. 그리고 이를 마스크로 기억한 다음,

컴파일러 룩업테이블 최적화를 위해 switch-case문으로 분기를 작성합니다.

원래 하드코딩이 성능은 더 잘나온다고 들었습니다(?)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

switch (mask)
{
	case 0b0000'0000:break; // 평범한 케이스

	//이하 다 비정상 : 다른처리해야함
	case 0b0000'0001:break;
	case 0b0000'0010:break;
	case 0b0000'0100:break;
	case 0b0000'1000:break;

	case 0b0000'0011:break;
	case 0b0000'0101:break;
	case 0b0000'1001:break;
	case 0b0000'1010:break;
	case 0b0000'1100:break;
	case 0b0000'0110:break;

	case 0b0000'0111:break;
	case 0b0000'1011:break;
	case 0b0000'1101:break;
	case 0b0000'1110:break;

	case 0b0000'1111:return LinearColor::Error;

}

기본적인 4점 모두 존재하는 경우(0000)에 대해서는 Bilinear-interpolation은 다음과 같습니다.

1

Lerp(Lerp(좌하단, 우하단, x무게중심), Lerp(좌상단, 우상단, x무게중심),y무게중심)

코드로 변환하면 다음과 같이 작성할 수 있습니다.

1

case 0b0000'0000: return Math::Lerp(Math::Lerp(_Buffer[ff], _Buffer[cf], xBary), Math::Lerp(_Buffer[fc], _Buffer[cc], xBary), yBary);

앗! lerp함수가 제대로 동작하지 않는 것 같으니 바꿔줍니다.

어짜피 똑같은 식이지만, 연산자 오버라이드에 대해 조금 더 안전해질 수 있도록

T * float 의 형태를 취하게 바꿔줍니다.

1
2
3
4
5
6
7
8

template< class T>
FORCEINLINE static constexpr T Lerp(const T& InSrc, const T& InDest, float InAlpha)
{
	//return (T)(InSrc + InAlpha * (InDest - InSrc));
  // == (T)(InSrc +  (InAlpha * InDest - InAlpha * InSrc)); 
  // == (T)(InSrc - InAlpha * InSrc + InAlpha * InDest ); 
	return (T)(InSrc * (1 - InAlpha) + InDest * InAlpha);
}

이제 텍스처를 준비해서 돌려봅시다.

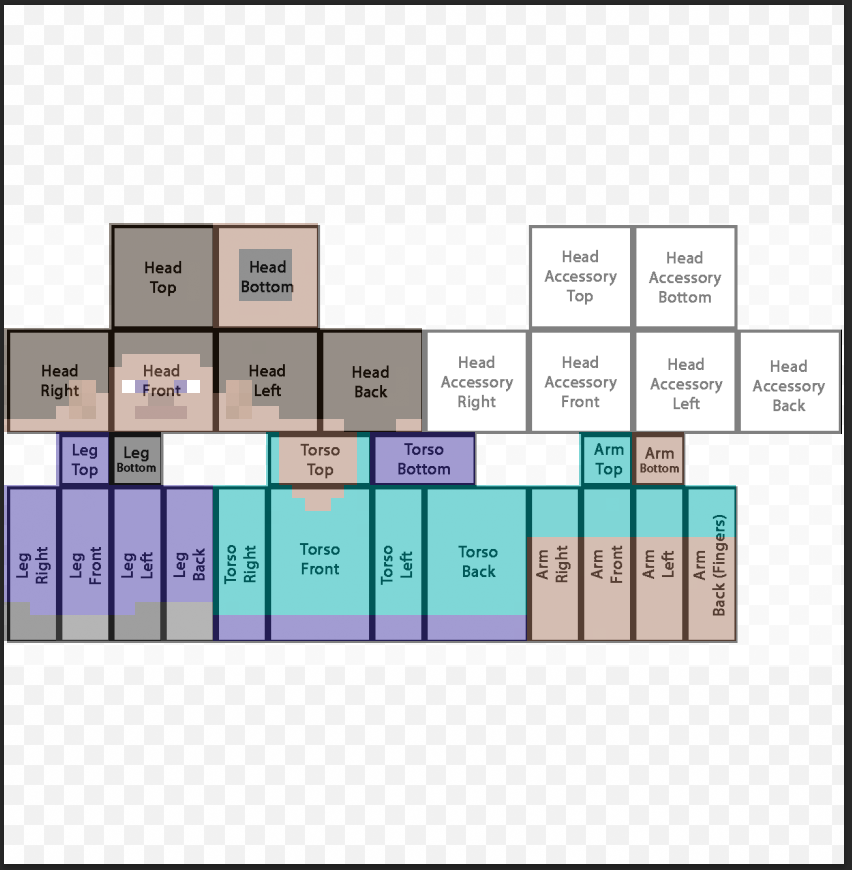
12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%207.png

텍스쳐입니다.

원본 소스

12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%208.png

최종본

12%20Local%20Space,%20Texture%20Mapping,%20Bilinear%20Interpol%20c97b516b9cde4e0385aa15bd8647f054/Untitled%209.png

오 제대로 흐릿하게 보이기 시작합니다.

그리고 특유의 작은 텍스처를 사용할 때 가장 외각쪽 선에

다른 색상이 묻는 그 현상도 볼 수 있습니다!

(그래서 텍스처를 그릴때 조금 넉넉하게 그려야 하죠)

(라이트맵에서 패딩도 넉넉하게 줘야 하고요)

그리고 이걸 구현하며 깨달은게… 처음 캐릭터의 UV좌표를 좀 잘못 설정한 것 같습니다.

몸통에 파란거 묻는걸 보니 TorsoRight 및 TorsoLeft까지 영역으로 잡힌 것 같습니다.

아마 팔도..조금 잘못된 것 같습니다. 아무렴 어떤가요 하하!

마지막으로 전체코드 한번 보고 마무리하겠습니다.

Implement Bilinear Interpolation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

LinearColor Texture::GetSample(Vector2 InUV) const
{
	if (!IsIntialized())
	{
		return LinearColor::Error;
	}

	//Implement Bilinear Interpolation

	int x = Math::FloorToInt(InUV.X * _Width - 0.5f) % _Width;
	int y = Math::FloorToInt(InUV.Y * _Height - 0.5f) % _Height;

	float xBary = Math::Clamp(fmod((InUV.X * _Width - 0.5f), _Width) - x, 0.0, 1.0);
	float yBary = Math::Clamp(fmod((InUV.Y * _Height - 0.5f), _Height) - y, 0.0, 1.0);

	//current index
	//int index = _Width * (_Height - (1 + y)) + x;

	int indexs[4];
	const int& ff = indexs[0] = _Width * (_Height - (1 + y)) + x;
	const int& cf = indexs[1] = _Width * (_Height - (1 + y)) + x + 1;
	const int& fc = indexs[2] = _Width * (_Height - (1 + y + 1)) + x;
	const int& cc = indexs[3] = _Width * (_Height - (1 + y + 1)) + x + 1;
	
	__int8 mask = 0; // 0b0000' | cc | fc | cf | ff |
	
	for (int i = 0; i < 4; ++i)
	{
		if(indexs[i] >= _Buffer.size())
		{
			mask |= 1 << i;
		}
	}

	switch (mask)
	{
		//내부 점
	case 0b0000'0000: return Math::Lerp(Math::Lerp(_Buffer[ff], _Buffer[cf], xBary), Math::Lerp(_Buffer[fc], _Buffer[cc], xBary), yBary);

		//짜고 보니... 논리적 존재 불가
	//case 0b0000'0001: return Math::Lerp(_Buffer[cf],								 Math::Lerp(_Buffer[fc], _Buffer[cc], xBary), yBary);
	//case 0b0000'0010: return Math::Lerp(_Buffer[ff],								 Math::Lerp(_Buffer[fc], _Buffer[cc], xBary), yBary);
	//case 0b0000'0100: return Math::Lerp(Math::Lerp(_Buffer[ff], _Buffer[cf], xBary), _Buffer[cc],							yBary);
	//case 0b0000'1000: return Math::Lerp(Math::Lerp(_Buffer[ff], _Buffer[cf], xBary), _Buffer[fc],							yBary);

		//각 최외각 선
	case 0b0000'0011: return Math::Lerp(_Buffer[fc], _Buffer[cc], xBary);
	case 0b0000'0101: return Math::Lerp(_Buffer[cf], _Buffer[cc], yBary);
	case 0b0000'1010: return Math::Lerp(_Buffer[ff], _Buffer[fc], yBary);
	case 0b0000'1100: return Math::Lerp(_Buffer[ff], _Buffer[cf], xBary);

		//각 구석.
	case 0b0000'0111: return _Buffer[cc];
	case 0b0000'1011: return _Buffer[fc];
	case 0b0000'1101: return _Buffer[cf];
	case 0b0000'1110: return _Buffer[ff];

		// 논리적 존재불가
	case 0b0000'0001:
	case 0b0000'0010:
	case 0b0000'0100:
	case 0b0000'1000:
	case 0b0000'1001:
	case 0b0000'0110:
	case 0b0000'1111:
		return LinearColor::Error;

	}

	return LinearColor::Error;

	//end Implement Bilinear Interpolation

	//original source
	//int x = Math::FloorToInt(InUV.X * _Width) % _Width;
	//int y = Math::FloorToInt(InUV.Y * _Height) % _Height;
	//int index = _Width * (_Height - (1 + y)) + x;
	//if (index >= _Buffer.size())
	//{
	//	return LinearColor::Error;
	//}

	//return _Buffer[index];
}

생각해보니 어짜피 _Buffer.size() 검사를 굳이 저렇게 각 위치에 대해 했어야했나 싶습니다.

뭐 호출 안되는 코드라면 컴파일러가 잘 최적화 해주겠죠. 하하.

느낀점

삼선형 필터링(Trilinear interpolation)은 아마 이렇게 동작하지 않을까? 라고 생각한 부분이

유사하게 동작해서 재미있었습니다.

구현하는데 재미있어서 시간이 빨리갔습니다.

그런데 점을 하나하나 찍다보니 디버깅하는데는 엄청 힘듭니다.

아무튼 어쨋든

끝!

잡다한 이야기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

	int indexs[4];
	const int& ff = indexs[0] = _Width * (_Height - (1 + y)) + x;
	const int& cf = indexs[1] = _Width * (_Height - (1 + y)) + x + 1;
	const int& fc = indexs[2] = _Width * (_Height - (1 + y + 1)) + x;
	const int& cc = indexs[3] = _Width * (_Height - (1 + y + 1)) + x + 1;
	
	__int8 mask = 0; // 0b0000' | cc | fc | cf | ff |
	
	for (int i = 0; i < 4; ++i)
	{
		if(indexs[i] >= _Buffer.size())
		{
			mask |= 1 << i;
		}
	}

이 코드가 살짝 걸리는데,

단지 마스크 체크를 위한 배열을 사용하고,

밑에서는 사용하지 않습니다.

흑마법(?)을 생각한다면, ff cf fc cc를 모두 한번에 선언하여

메모리를 점프(interval = &ff - &fc, p += interval)해서

for-loop에서 접근할 수 있을 것 같습니다.

아니면 그냥 하드코딩하는게 나을 것 같네요.

CK, 그래픽 프로그래밍 2D, assignment
This post is licensed under CC BY 4.0 by the author.
Contents