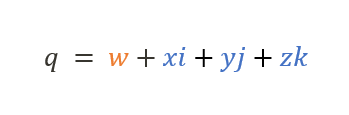11. Euler & Quaternion

Euler & Quaternion

머릿말

---

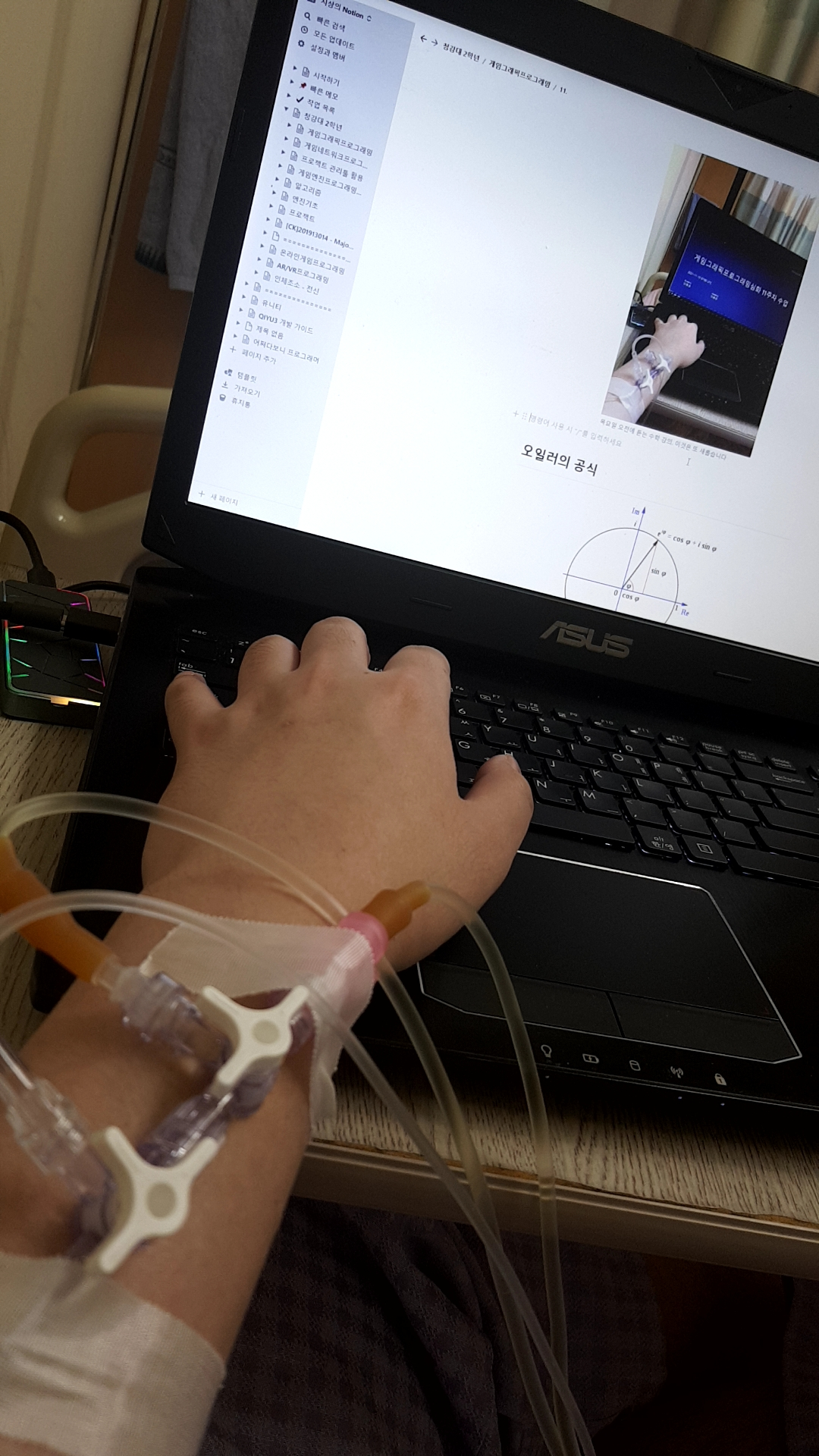
수업을 들으려 했지만 마약성 진통제에 취해서 눈떠보니 이미 수업이 끝난 뒤였습니다…

그렇게 저는 프로젝트 크리틱도, 수학도 듣지 못했습니다

목요일 오전에 듣는 수학 강의. 이것은 또 새롭습니다

그리고 추가되는 선들(유선 불편)

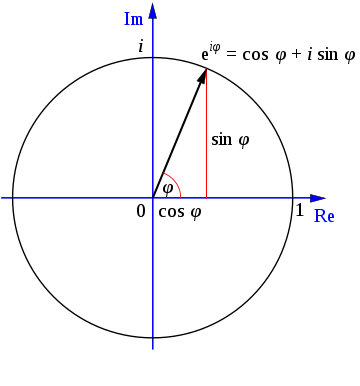
오일러의 공식

---

오일러의 공식

비판정을 사용한 자연지수함수, sin함수, cos함수의 멱급수

---

자연지수함수

저번주에 자연지수함수는 멱급수 표현이 가능하다고 나타냈었죠?

$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+ \cdot\cdot\cdot =\sum_{n=0}^{\infin}\frac{x^n}{n!}$$

비판정을 통해 확인해 봅시다.

$$L=\lim_{n\to\infty}\frac{\frac{x^{n+1}}{(n+1)!}}{\frac{x^n}{n!}} =\lim_{n\to\infty}\frac{x}{n+1} =x \cdot \lim_{n\to\infty}\frac{1}{n+1} = 0$$

sin 함수 & cos 함수

둘 다 비슷한 함수니까 한방에 묶었습니다. 같이보면 재미있어요.

두 함수 모두 멱급수로 표현하면 다음과 같은데,

$$f(x)=f(0)+ \frac{f'(0)}{1!}x+ \frac{f''(0)}{2!}x^2+ \frac{f'''(0)}{3!}x^3+ \cdots$$

저번주에 진행했던 사인함수와 코사인함수의 미분을 고려해봅시다

$$f(x) = sin(x), f'(x) = cos(x)\\ g(x) = cos(x), g'(x) = -sin(x)$$

즉 cos함수에서 sin함수로 변환할 때에만 부호변환이 발생하며,

.. → cos → sin → cos → sin → …의 꼴로 감을 알 수 있습니다.

또한 sin의 경우 sin(0) = 0을 고려하여 두 식을 위의 멱급수로 표현한다면

$$sinx=0 +\frac{1}{1!}x+-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+ \frac{1}{9!}x^9+\cdots \\ cosx=1\space-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+\frac{1}{8!}x^8+\cdots$$

이렇게 볼 수 있습니다.

비판정의 시간입니다. 이건 조금 더 플머스럽게 묶어보았습니다. 하하.

결국 더 작은 팩토리얼은 더 큰 팩토리얼에 의해 사라지고, 그 위에부분만 남으니까

$$\prod_{k=low+1}^{high}\left(\frac{1}{2n+k}\right)$$

이렇게 표현을 한다면,

$$let, l = (sin :1, cos : 0), h = (sin : 3, cos : 2)\\\space \\ L=\lim_{n\to\infty}\left\vert \frac{\frac{(-1)^{n+1}x^{2n+h}}{(2n+h)!}}{\frac{(-1)^nx^{2n+l}}{(2n+l)!}}\right\vert =\lim_{n\to\infty}\left\vert {\frac{(-1)^{n+1}x^{2n+h}}{(2n+h)!}}\cdot{\frac{(2n+l)!}{(-1)^nx^{2n+l}}}\right\vert \\ =\vert x^2\vert \cdot\lim_{n\to\infty} \vert \frac{(2n+l)!}{(2n+h)!}\vert =\vert x^2\vert \cdot\lim_{n\to\infty}\frac{(2n+l)(2n+l - 1)\cdots(2n-1)(2n-2)\cdots}{(2n+h)(2n+h-1)\cdots(2n+1)(2n)\cdots} \\=\vert x^2\vert \cdot\lim_{n\to\infty} \prod_{k=l+1}^{h}\left(\frac{1}{2n+k}\right)\\= 0$$

허수단위 i를 사용해 세 함수의 멱급수를 서로 일치시키는 방법

---

$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\frac{x^6}{6!}+\frac{x^7}{7!}+\frac{x^8}{8!}+\cdot\cdot\cdot \\sinx=0 +\frac{x}{1!}+-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+\cdots\\cosx=1\space-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}+\cdots$$

자 아까 위에서 살짝 봤던 세개를 같은 형태로 놔두게 된다면 재미있는 규칙이 보입니다.

사인과 코사인 두개를 조합하면 e를 만들 수 있을 것 같아요.

그러나 sin의 3,7, …와 cos의 2,6..을 본다면 뭔가 부호가 있죠.

$$sin(x)+cos(x)=1+\frac{x}{1!}-\frac{x^2}{2!}-\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}-\frac{x^6}{6!}-\frac{x^7}{7!}+\frac{x^8}{8!}+\cdot\cdot\cdot$$

아직 써먹기 힘듭니다.

그런데 자연지수함수의 승수에 i를 붙이면 매우 놀라운 결과가 나옵니다.

$$e^{ix}=1+\frac{ix}{1!}-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+\frac{ix^5}{5!}-\frac{x^6}{6!}-\frac{ix^7}{7!}+\frac{x^8}{8!}+\cdot\cdot\cdot$$

어 그러면이제 i만 매 홀수항에 붙여주면 되겠네요?

홀수항이 sin이니 sin에 붙인다면?

$$isin(x)+cos(x)=1+\frac{ix}{1!}-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+\frac{ix^5}{5!}-\frac{x^6}{6!}-\frac{ix^7}{7!}+\frac{x^8}{8!}+\cdot\cdot\cdot$$

와 두 식이 일치합니다.

$$e^{ix} = cos (x)+isin(x)$$

오일러의 항등식에 대해 정리하시오.

---

그런데 여기서 x대신 $\pi$ 를 적용하면 어떻게 될까요?

$$e^{i\pi} = cos (\pi)+isin(\pi)\\ e^{i\pi} = -1 + 0 \\ e^{i\pi} + 1 = 0 \\$$

이걸 이제 중요한 상수 5개가 모두 들어있다하며 막 세상에서 가장 아름다운 수학 공식이라한다고 합니다.

그리고 이걸 오일러의 항등식이라 합니다.

…아름다운가요?

각 쎄타의 회전 변환을 수행하는 방법

---

이제 그렇다면 회전을 하나 더 추가할 수 있네요.

기저벡터를 통한 행렬을 통한 표현

$$\left[ \begin{matrix}cos\theta&-sin\theta\\ sin\theta&cos\theta \end{matrix} \right] \cdot \vec{(v_x,v_y)}$$

복소수를 통한 표현

$$\bold z = cos\theta + i sin\theta$$

(new)자연지수함수를 통한 표현

$$e^{ix}=cos\theta + i sin\theta$$

사원수 대수(Quaternion)

---

수강하며…

$$i^2=-1\quad j^2=-1\quad k^2=-1 \\i j k = -1$$

와 이 얼마나 놀라운 식입니까.

듣자마자 바로 놀랐습니다.

$$i j k = -1$$

와…. 어떻게 이렇게 와…. 와………..

듣자마자 아! 아!!!! 아!!!!!!!! …돌에다가 막 쓸만했다고 생각했습니다.

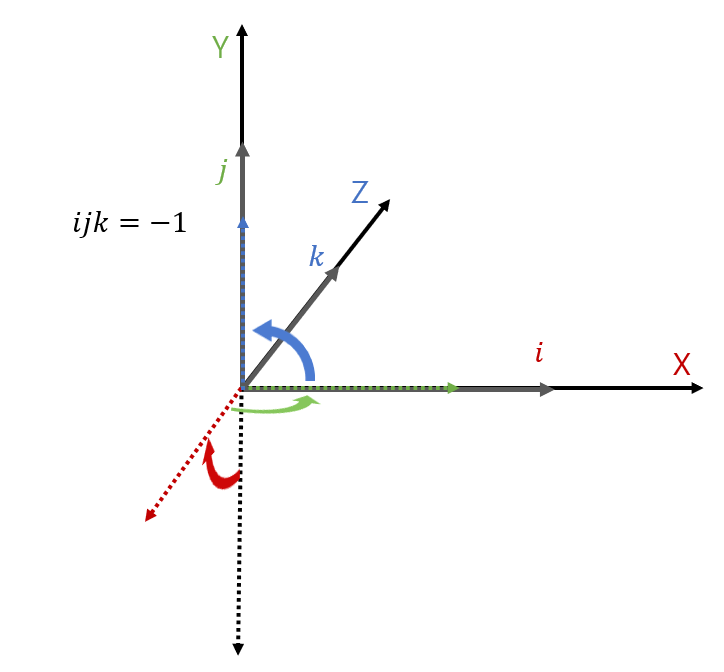
x y z 회전에 대해, 수 직선(x축)에서 -1로 되는건 z축으로 180도 회전,

즉 2차원 평면에서 회전한 것과 같습니다.

그리고 이건 y축으로 회전, x축으로 회전, 그 후 z축으로 회전한 것과 같은데,

즉 공통된 z축 회전을 제외하면 y축으로 회전 * x축으로 회전 = z축으로 회전 이라는 것입니다.

그러면 이게 무엇인가!

바로. 외적입니다. y축과 x축을 외적하면 z축이 나오므로, 해당축으로 회전을 돌린 것이라는 소리죠.

그렇습니다. i j k = -1.

놀랍고도 놀라운 식이였습니다.

그렇다면 이 곱은 외적인가요?

그렇다면 이 곱은 순서가 바뀐다면 반대 방향으로 (반수성질) 나타나게 되나요?

이 강의를 라이브로 수강하지 못한게 너무나도 안타깝습니다.

어쩌겠습니까… (합법적인 마약성분)진통제가 절 수업 끝날때 깨운것을…

사원수 곱셈 연산을 정리하시오.

---

$$ijk=-1\\ i^2=-1\quad j^2=-1\quad k^2=-1$$ $$iijk=i\cdot(-1)\quad-jk=-i\\\quad \therefore jk=i\\ \quad \\ ijkk=-1k\quad -ij=-k\quad \\\therefore ij=k\\ \quad \\ jk=i\quad jki=ii\quad jki=-1\quad jjki=j\cdot(-1)\quad \\\therefore-ki=jii\quad ki=j$$

하 이걸 참 수식으로 쓰니까 그 맛이 안나네요

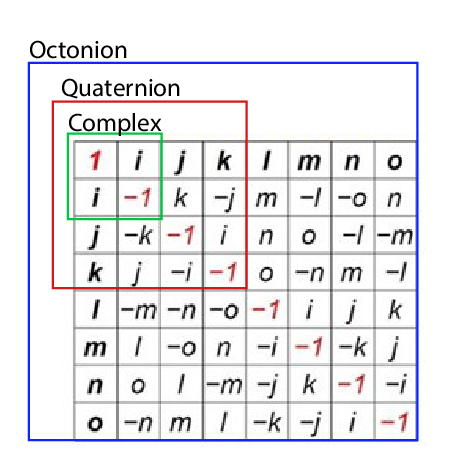
표로 정리해봅시다.

다시한번 꺼내봅시다

jk = i, kj = -i (외적과 유사하니까요) 앗 머리속에 짐벌락이 걸리셨나요? jk는 Z-, kj는 Y-에서 시작해주세요

그런데 표가 좀 별로네요. 더 세부적으로 정리해 봅시다.

(흡족) 순번은 아래로, 오른쪽으로, 입체적으로 입니다.

여기도 뭔가 성취수준이 높지 않아서 잡힐랑 말랑하는 무언가가 있네요.

아 그 참 거 하 ..

사원수를 실수부와 허수부로 구분하고 사원수 곱셈을 내적과 외적을 사용해 표현하시오.

---

사원수의 형태부터 봅시다.

드디어 파워포인트를 쓸 수 있어요! (대충 퇴원했다는 뜻)

사원수의 실수부(Scalar Part) : w

사원수의 허수부(Vector Part) : xi+yj+zk

이를 벡터로 표현한다면

$$q=w+xi+yj+zk\\ =(w,\vec{v})=(w,(x,y,z))$$

아하! 그래서 벡터 파트라고 하는거군요!

사원수의 곱을 내적과 외적으로 표현

$$let, q_1 = (w_1,(x_1,y_1,z_1)), q_2 = (w_2,(x_2,y_2,z_2))\\ q_1\cdot q_2\\ =(w_1w_2-x_1x_2-y_1y_2-z_1z_2)+(w_1x_2+x_1w_2+y_1z_2-z_1y_2)i+(w_1y_2-x_1z_2+y_1w_2+z_1x_2)j+(w_1z_2+x_1y_2-y_1x_2+z_1w_2)k\\$$

위 식에서 본다면, 앞의 실수부는 실수부의 곱에 벡터의 내적를 뺀 것이라 볼 수 있습니다.

그리고 이제 실수부의 항으로 다시 묶어서 정리를 한다면,

$$=(w_1w_2-(v_1\cdot v_2),(w_1(x_2i,y_2j,z_2k)+w_2(x_1i,y_1j,z_1k)+\\ ((y_1z_2-z_1y_2)i,(z_1x_2-x_1z_2)j,(x_1y_2-y_1x_2)k))\\$$

와 같이 볼 수 있네요.

그리고 마지막 맨 뒤의 부분은 외적과 같은 식이죠?

$$=(w_1w_2-(v_1\cdot v_2),(w_1\cdot v_2+w_2\cdot v_1+ v_1\times v_2))$$

묶어줍니다.

아 여기가 뭔가 잡힐듯 말듯 애매하네요.

사원수의 곱셈은 왜 교환법칙이 성립하지 않는지 정리

---

$$q_1\cdot q_2=(w_1w_2-(v_1\cdot v_2),(w_1\cdot v_2+w_2\cdot v_1+ v_1\times v_2))\\ q_2\cdot q_1=(w_2w_1-(v_2\cdot v_1),(w_2\cdot v_1+w_1\cdot v_2+v_2\times v_1))\\$$

다 정리하면 마지막 외적이 남죠?

네. 외적이 남는다는뜻은 교환법칙이 성립하지 않는다는 뜻입니다.

따라서 사원수의 곱셈은 교환법칙이 성립하지 않습니다.

내적은 모르겠고 자꾸 외적을 만나는게 마치 운명같네요. ijk = -1 … ijk = -1…..

순허수 사원수의 곱셈을 내적과 외적을 사용해 표현하시오.

---

순허수(Pure Imaginary Quarternion)

순허수가 뭔가 했네요. 실수부가 0인 사원수를 일컫습니다.

순허수 사원수의 곱셈

아까 식을 가져와 w들에 0을 넣어봅시다.

$$q_1\cdot q_2=(0\cdot 0-(v_1\cdot v_2),(0\cdot v_2+0\cdot v_1+ v_1\times v_2))\\ =(-(v_1\cdot v_2),( v_1\times v_2))$$

실수부는 두 사원수의 허수부의 내적의 반수(反數)입니다.

허수부는 두 사원수의 허수부의 외적입니다.

그러면 순허수의 사원수의 곱셈은 내적은 여전히 교환법칙을 성립하고, 외적은 반수성질이 존재하므로, 순허수의 사원수의 교환은 외적의 교환과 같이 방향이 반대로 됩니다!

ijk….

켤레사원수를 사용해 사원수의 크기를 구하는 방법을 정리하시오.

---

사원수의 크기(노름)

사원수의 크기는 복소수,벡터 등의 크기를 구하는 방법과 비슷하게 정의됩니다.

$$\vert q\vert = \sqrt{x^2+y^2+z^2+w^2}$$

켤레사원수 (Conjugate)

켤레 사원수는 켤레복소수와 마찬가지로 허수부의 값이 반수(反數)인 사원수를 의미합니다

표현법으로는

$$q^*,\bar{q},q^t,\tilde{q}$$

가 있습니다.

일반적으론 $q^*$ 을 쓴다고 하네요. 복소수때 $\bar{z}$ 썼었는데 괜히 그렇게 했습니다.

아무튼 그렇고, 따라서 켤레사원수는 다음과 같이 볼 수 있습니다.

$$let, \vec{v}=(x,y,z) \\q=(w,\vec{v})\quad\space\ q^*=(w,-\vec{v})$$

켤레사원수의 성질

$$(q^*)^*=q\\ (pq)^*=q^*p^*\\ q^*q=qq^*=ww+(\vec v\cdot \vec v)=\vert q\vert ^2$$

마지막 식은 좀 헷갈릴 수 있습니다.

그래서 풀어보았습니다.

$$(ww-(v\cdot -v),(w\cdot v+w\cdot -v+v\times v))\\ =ww+v\cdot v=ww+xx+yy+zz=\vert q\vert ^2$$

켤레사원수를 통한 사원수의 크기

위 식에서 ww xx ..를 보면 알듯, 그냥 복소수처럼 하면 됩니다.

$$\sqrt{qq^*}=\sqrt{\vert q\vert ^2}=\vert q\vert$$

사원수의 회전

---

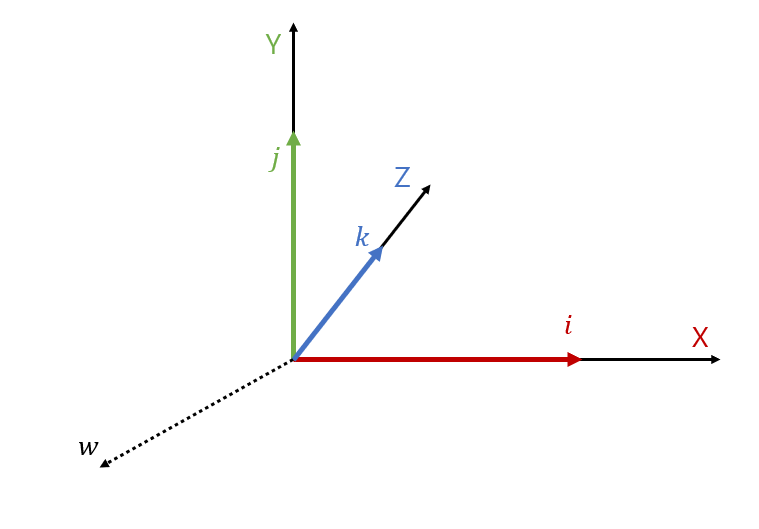
3차원 공간을 사원수로 표현하는 방법을 정리하시오.

---

일단 직교하는 4개의 축을 그린다는 것은 있을 수 없습니다.

아, 가능할진 몰라도 일단 제 뇌에서는 안됩니다.

그래서 일단 실수부를 제외한 3개의 축을 가진 허수부를 유클리드 공간에 표현합니다.

실수부는 따로 두고요.

이때 i,j,k는 각 x,y,z축에 대응하고, 실수부가 0인 순허수 사원수는

3차원 공간의 벡터에 대응한다고 볼 수 있는겁니다.

헉 그런데 이걸 보니까 확실히 편하네요. 첫번째 곱은 축회전이 아닌 바로 적용이라고 생각한다면 …

오일러 공식에 사용할 수 있는 사원수의 조건을 정리하시오.

---

$$e^{ix} = cos(x)+i\cdot sin(x)$$

위의 오일러 공식을 만족시키기 위해서는 i에 대한 전제조건이 필요합니다. 바로,

$$i^2 = -1, \vert \vert i\vert \vert ^2 = 1$$

이라는 부분이죠.

어, 제곱하면 -1이고 노름의 제곱이 1인 값?

그것은 바로 아까 회전 계속 굴리던 그친구들이 아닐까요?

사원수의 조건

위의 내용을 다시 잘 읽어보면 됩니다.

• 순 허수여야하고
• 노름의 제곱이 1이여야 하며
• 제곱하여 -1이 되면 됩니다.

그렇다면 ‘단위 순허수 사원수’가 되겠네요

단위 순허수 사원수(Unit Pure Imaginary Quaternions ? )

$$\hat{u} = (0,\hat v), \vert \vert \hat{u}\vert \vert =1 \\ \hat{u} \cdot \hat{u} = x^2i^2 + y^2j^2 + z^2k^2 =-1$$

오일러 공식으로부터 회전을 수행하는 회전 사원수의 형태를 정리하시오.

---

$$e^{\hat{u}x}=cos\theta+\hat{u}\cdot sin\theta=(cos\theta,\hat{u}\cdot sin\theta)$$

회전 사원수를 사용해 3차원 공간의 벡터를 회전시켰을 때 발생하는 문제점을 정리하시오.

---

3차원공간의 벡터를 순허수 사원수로 표현하여 회전, 즉 곱셈 연산을 시켰다면,

다음과 같은 꼴로 볼 수 있습니다.

$$(cos\theta,u\cdot sin\theta) \cdot (0,\vec{v})$$

이걸 계산하게 되면 실수부에 값이 생기게 되는데,

실수부에 값이 생겼다는 것은 3차원 공간에 표현할 수 없다 가 되므로 …. 무언가 다른 방법이 필요하겠죠.

마치며

---

아 뭔가 전부 다 뭔가 잡힐랑말랑하는 그 Unit이 아닌 값들의 관계에 대한 그 상관관계가 뭔가 아 그 참 .. 진짜 유레카!!! 하는게 ijk=-1밖에 없어서 너무 아쉽습니다.