Convex, Line Clipping,Mesh

절단 - 코핸서덜랜드 라인클리핑 알고리즘

(Cohen-Sutherland line clipping algorithm)

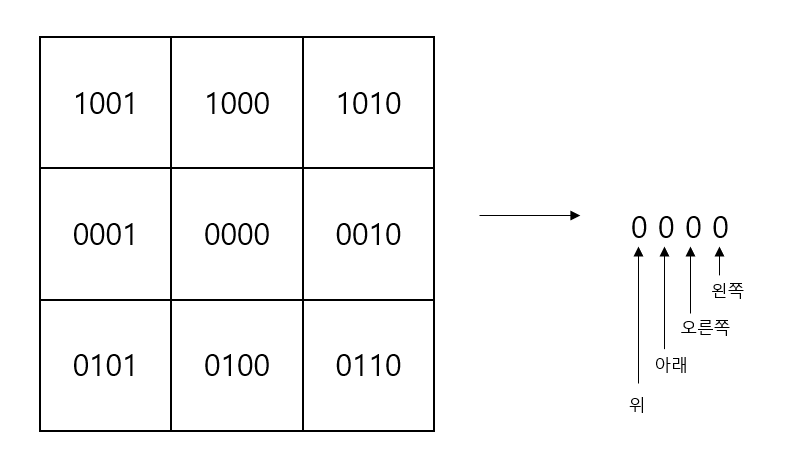
11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled.png

코핸 서덜랜드 라인 클리핑 알고리즘은 원래 화면영역을 가운데에 두고 각 화면을 벗어난 영역을 나누는 것에서 시작합니다.

각 영역을 위, 아래 ,오른쪽, 왼쪽에 해당하는 4비트 데이터로 나누어 어느 영역에서 어느영역에 걸치는 지에 대한 판별을 진행합니다.

이때 & (AND operation, 논리곱)을 사용하여 판별하게 되는데,

만약 각 성분 (위,아래,오른쪽,왼쪽)에 대하여 같은 위치에 있다면 1을, 아니라면 0의 값을 얻는 것을 통해 진행합니다.

이를 다시 정리하면 다음과 같은 케이스로 나눌 수 있습니다.

Point A = Point B = 0000 (Point A | Point B = 0000) 이 경우, 완전히 두 점이 화면 내부에 있다고 판별합니다.
Point A & Point B = 0000 양 점이 화면 외부에 있지만, 서로 같은 위치가 아닌 경우입니다. 추가적인 연산이 필요합니다.
Point A & Point B ≠ 0000 이 경우는 두 점이 화면 외부에 있으므로 제거합니다.
Point A ≠ 0000, Point B = 0000 한 점이 화면 내부에, 나머지 한 점이 화면 외부에 있을 경우입니다. 추가적인 연산이 필요합니다.

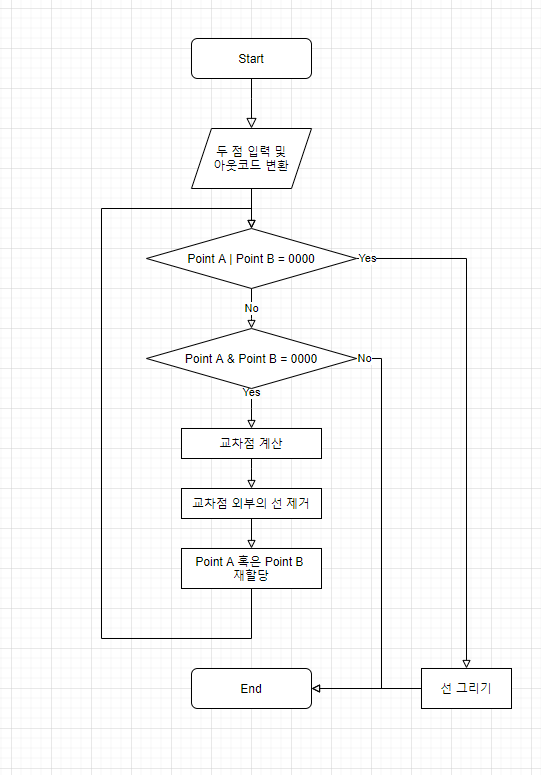
만약 이 때, Case 2, Case 4에 대해서는 교차점 계산을 진행하여 두 점을 얻은 후,

두 점을 한번 더 어느 영역에 위치하는지 검사하고 화면안에 있는 선분만 얻을 수 있게 됩니다.

교차점은 단순히 기울기를 얻은 후, 얻고자하는 축이 아닌 나머지 하나의 축 좌표를 통해 쉽게 구할 수 있습니다. 삼각형의 닮음을 통한 비례식을 사용하는 것과 같습니다.

플로우차트로 정리하면 다음과 같습니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%201.png

일직선상에 위치하지 않은 세 점의 아핀조합 결과

아핀조합

(중략) 그래서 계산 결과값의 z성분이 1이 되도록 해야하죠.

이걸 잘 기억하면서 선형조합을 생각해본다면,

세 점의 아핀 조합 결과는 다음과 같이 정의 할 수 있습니다.

$P'=s\cdot P_1+t\cdot P_2 +(1-s-t)\cdot P_3$

그리고 특정 점을 뺀, 변위벡터를 통해 이를 나타낸다면

$P'-P_3=s(P_1-P_3)+t(P_2-P_3)$

로 나타낼 수 있습니다.

결론적으로 변위 벡터 = 벡터 + 벡터 이므로 이때 두 벡터가 선형독립이라면

두개의 기저벡터를 통해 만들 수 있는 차원이므로

이때 생성된 점은 $P_3$ 을 기준으로 2차원 변위 벡터를 더했으므로,

즉 세 점의 아핀 조합으로 생성된 모든 점은 동일한 평면에 위치합니다.

컨벡스 및 컨벡스 조합 (Convex & Convex Combination)

컨벡스(Convex)는 라틴어 convexus를 어근으로하는 vaulted or arched, 즉 볼록한 이라는 형용사입니다.

어떤 집합안에서 두개의 지점을 선으로 연결했을 때, 선을 이루는 요소들이 그 집합속에 속해있다면 그 집합을 Convex Set이라고 합니다.

7주차에 Linear Interpolate에 대해 적었던게 있습니다.

$P = Lerp(P_1,P_2,a)\\ P = (1-a)*P_1 + a*P_2;$

여기서 $a$ 의 범위를 $0≤a≤1$ 로 제한하는 아핀 조합을

컨벡스 집합(convex set)이라 볼 수 있겠네요.

왜 그럴까요? $0≤a≤1$ 의 경우, 두 점의 사이에서만 새로 생성될 수 있으며,

이 조합에서 두 점은 최대의 변위를 갖기 때문입니다.

시각적으로 확인한다면 다음과 같습니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%202.png

그러면 아까 위에서 설명한 세 점의 아핀조합에서 해당 컨벡스 조합을 시각화 한다면 어떻게 될까요?

$P = (1-a)*P_1 + a*P_2;\\ P = (1-s-t) \cdot P_1 + s\cdot P_2 + t \cdot P_3$

다음과 같이 두가지 인자 s,t에 대해

0≤s≤1,\quad 0≤t≤1,\quad 0≤(1-s-t)≤1

의 제한을 걸어준다면

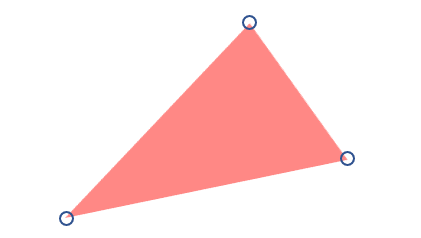
11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%203.png

아마 다음과 같은 삼각형의 공간 속에서만 생성될 것이라 생각합니다.

이렇게 주어진 점을 연결한 도형 내부에 속하는 지점을

컨벡스 조합(convex combination)이라 합니다.

3차원 물체의 기본단위는 왜 삼각형?

3차원의 물체를 표현하는 방법은 크게 두가지가 있다고 생각합니다.

물체 표면만 나타내는 경우와
물체 내부까지 표현하는 경우

그 중 많이, 그리고 주로 사용되는 경우는 물체의 표면만 나타내는 경우인데,

아무래도 실제 보이는 것은 표면인 경우가 더 많기 때문이라고 생각합니다.

즉, 물체를 표현할 때 입체가 아닌 면으로 표시하게 되는데, 면을 구성하는 가장 작은 단위가 삼각형이기 때문에 3차원 물체의 기본 단위는 삼각형이라고 볼 수 있습니다.

삼각형이 아닌 사각형을 사용하는 경우가 간혹 있지만, 실질적으로 작업 이후 컴퓨터가 처리할 때는 삼각형으로 변경해서 처리합니다.

이 때, 크게 삼각형을 통해 그리는 방법들은 다음과 같은 방법들이 있습니다

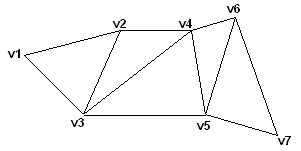
Triangle Strip

한붓그리기와 같은 방식입니다. 메모리와 처리시간을 효율적으로 사용할 수 있습니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%204.png

Triangle Fan

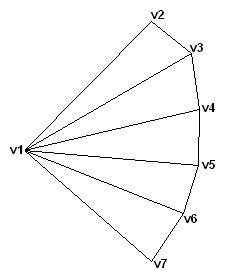
11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%205.png

Triangle List

비 연속적인 삼각형 조각으로 구성된 개체를 만듭니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%206.png

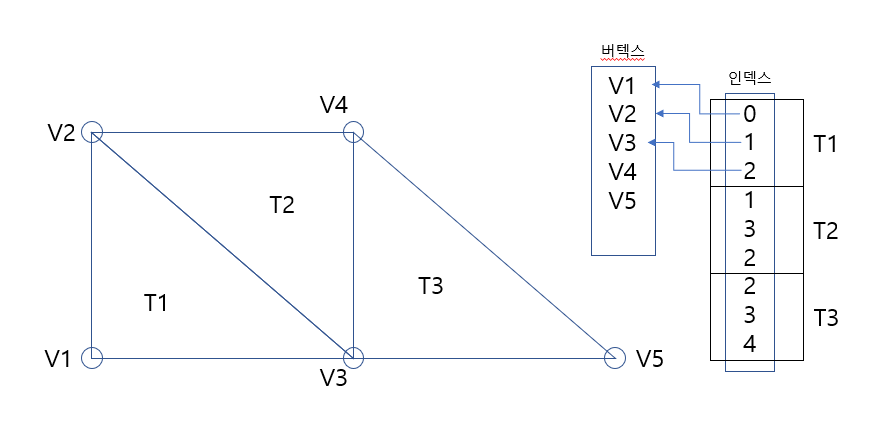
트라이앵글 리스트 방법으로 메시를 표현하는 방법 정리

간단하게 설명하자면 버텍스 리스트, 즉 점 리스트를 그냥 던져주면 됩니다.

이후 점을 버텍스(정점)이라고 기술하겠습니다.

삼각형 하나를 그리기 위해 3개의 버텍스가 필요하며,

총 삼각형 개수 * 3 개의 버텍스가 필요합니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%204.png

다만 이렇게 될 경우 Triangle Strip 기준 7개의 정점으로 구성된 삼각형 리스트를 그릴때, v2 ~ v6의 경우 버텍스가 중복되어 총 15개의 버텍스가 필요하게 됩니다.

이를 해결하기 위해 버텍스 리스트를 따로두고, 삼각형을 그리기 위해 필요한 버텍스를

인덱스를 통해 접근하여 버텍스를 중복으로 저장하는 경우를 해결합니다.

11%20Convex,%20Line%20Clipping,Mesh%20ebcc20c2d47f493aa66a637b654d8cdf/Untitled%207.png

무게중심 좌표가 가지는 의미와 특징

자 과거로 돌아가서, 컨벡스 및 컨벡스조합에서 계속 나아가 봅시다.

아까 보았던 새로운 점을 생성하는 식을 볼까요?

P = (1-a)*P_1 + a*P_2;\\ P = (1-s-t) \cdot A + s\cdot B + t \cdot C

이때 a를 (선에서 의) 무게 중심 좌표(Barycentric coordinate)라고 합니다.

또한 s와 t를 삼각형의 무게 중심 좌표(Barycentric coordinate) 라고 합니다.

그러면 무게중심 좌표가 가지는 의미랑 특징은 무엇일까요?

어느 점의 비중이 더 큰가, 혹은 어느점에 더 가까운가 라고 생각하면 편할 것 같습니다.

마치 엔진에서 사용하는 프로브 블렌딩을 할때의 가중치, 혹은 리깅을 할때 버텍스가 어떤 본에 더 영향을 받는지에 대한 가중치와 같은 개념입니다.

위에서 설명했던 것을 수학적으로 다시 정리하자면

P = a_1P_1 + a_2P_2 + ... +a_nP_x\\ \Sigma{a_n} = 1,\quad 0 \leq a_n \leq 1

다음과 같이 나타낼 수 있으므로, 각 성분 a에 대해 0≤a≤1의 범위에 있다면 내부에 있음을 알 수 있습니다.

내적을 사용해 삼각형과 같은 평면에 위치한 점의 무게중심 좌표계를 구하는 수식 정리

계속해서 자꾸 예전에 적어둔 식을 가져오게 되네요.

하하 다 같은개념에서 시작해서 그렇습니다.

내적을 다시 기억해봅시다.

따라서,
곱셈의 교환법칙이 성립하므로, 내적의 교환법칙 역시 성립한다.
두 식이 같지 않으므로, 내적의 결합법칙은 성립하지 않는다.
덧셈의 교환법칙이 성립하므로, 내적의 분배법칙은 성립한다.

$[P'-P_3=s(P_1-P_3)+t(P_2-P_3)\\ \vec{w} = s \cdot \vec{u} + t \cdot \vec{v}](/posts/11-Convex,-Line-Clipping,Mesh-ebcc20c2d47f493aa66a637b654d8cdf/)$

여기서부터 다시 시작해봅시다.

한 점에서 부터 시작되는 양 변으로 향하는 두 벡터에 대해 유사도(편의상 다음과 같이 말하겠습니다)를 검사하기 위해 양변에 $u,v$ 를 내적합니다

w \cdot u = s(u \cdot u) + t(v\cdot u)\\ w \cdot v = s(u \cdot v) + t(v\cdot v)

그런데 저희는 $s,t$ 를 구해야하므로, 하나의 식을 소거하기위한 식을 만듭니다.

일단 $s$ 부터 구해봅시다

두 식을 빼서 $s$ 를 구하기 위해선, 양 식에 $v \cdot v , u \cdot v$ 를 곱해줍니다.

(w \cdot u)\cdot(v\cdot v) = s(u \cdot u)\cdot (v\cdot v) + t(v\cdot u)\cdot (v\cdot v) \\ (w \cdot v)\cdot (u\cdot v) = s(u \cdot v)\cdot (u\cdot v) + t(v\cdot v)\cdot (u\cdot v)

두 다항식을 뺀 후, $s$ 에 대해 정리하면

s = \frac{(w\cdot u)\cdot (v\cdot v) - (w\cdot v)\cdot (u\cdot v)} {(u\cdot u)\cdot (v\cdot v)-(u\cdot v)\cdot (u\cdot v)}

같은 방법으로 $t$ 에 대해서도 정리해줍니다.

t = \frac{(w\cdot v)\cdot (u\cdot u) - (w\cdot u)\cdot (v\cdot u)} {(u\cdot u)\cdot (v\cdot v)-(u\cdot v)\cdot (u\cdot v)}

이제 이 식을 통해 평면에 위치한 점의 무게중심 좌표계를 만들 수 있으며,

이 무게중심 좌표의 각 성분에 대해 0보다 크고 1보다 작은지에 대해 검사한다면,

삼각형에 포함되는 점. 컨벡스 조합인지 판별 할 수 있습니다.

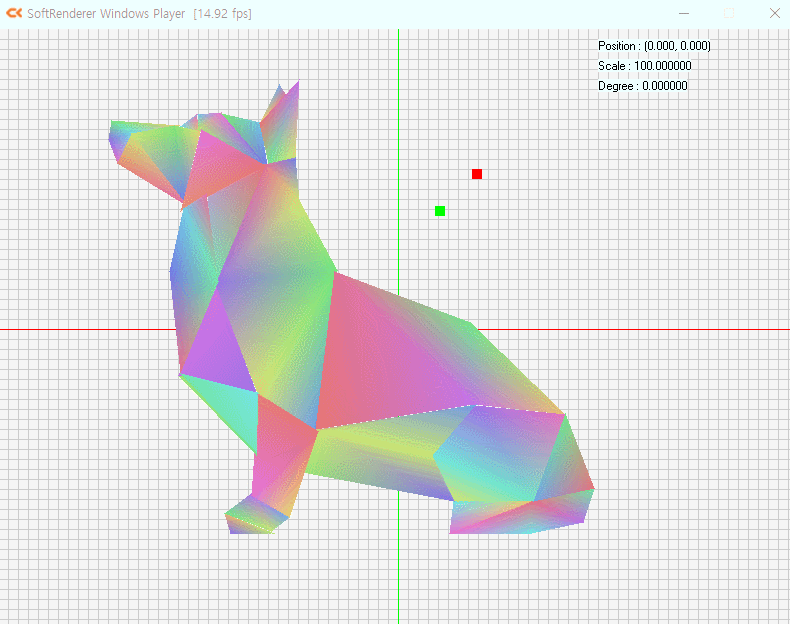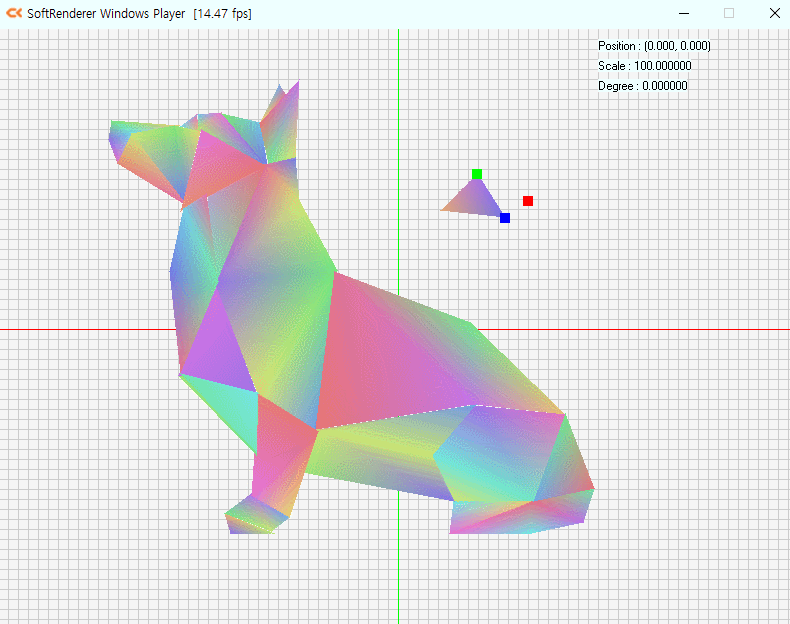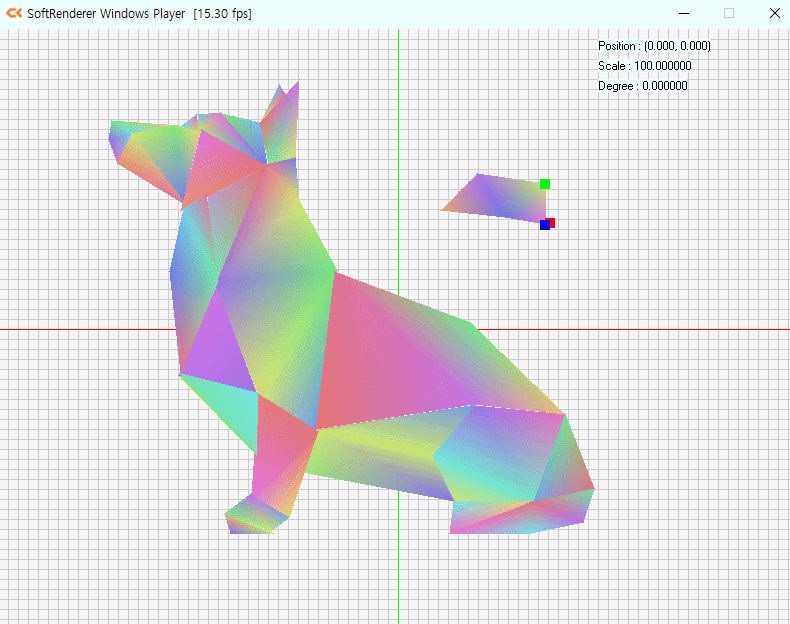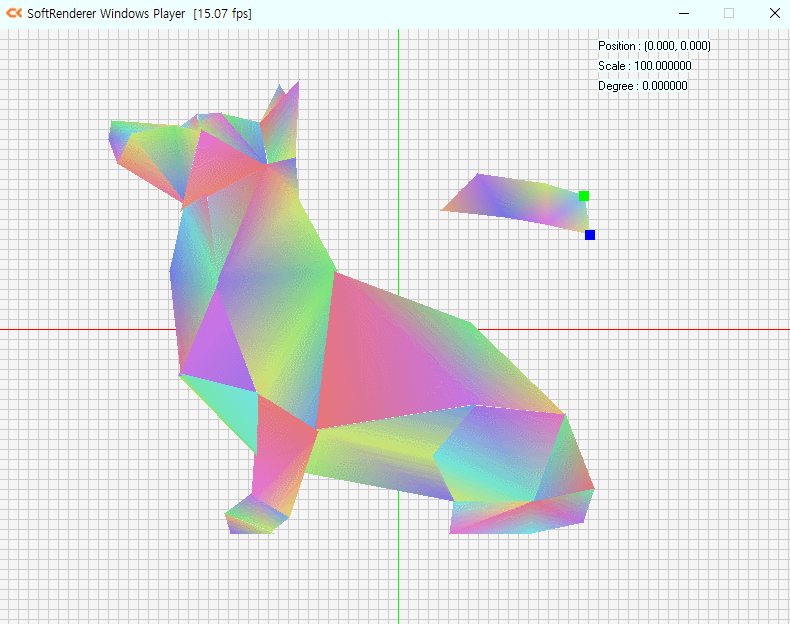
예제를 기반으로 메시를 설계하고 구현.

무게중심 좌표를 이용해 내부 채색

저번주차 과제에 이어서 작업을 해보도록 하였습니다.

입력을 진행할 때 마다 버텍스가 하나씩 추가되므로,

Triangle List 보다는 Triangle Strip이 더 적합하다고 생각하였습니다.

따라서 인덱스 버퍼를 구현하지 않는,

렌더링은 Triangle Strip 기반으로 작업을 진행합니다.

방향키로 이동하여 삼각형을 찍습니다.

색상은 무게중심 좌표계를 통해 각 버텍스의 색상을 받아옵니다

예시는 Triangle Strip로 그리다보니 한계가 있어서 겹쳐서 그린 것이 좀 있습니다.

  
// 게임 로직과 렌더링 로직이 공유하는 변수
std::vector<Vector3> list;
Vector3 point(0.f, 0.f, 0.f);
Vector3 lastPoint(0.f, 0.f, 0.f);
Vector3 lastLastPoint(0.f, 0.f, 0.f);
Vector2 lastInput;

bool lastCommit = false;
bool lastRCommit = false;

// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
	// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& g = Get2DGameEngine();
	const InputManager& input = g.GetInputManager();

	const float HueShiftRate = 60.f;

	auto xAxisRaw = input.GetAxis(InputAxis::XAxis) * InDeltaSeconds;
	auto yAxisRaw = input.GetAxis(InputAxis::YAxis) * InDeltaSeconds;
	auto hue = InDeltaSeconds * HueShiftRate;

	
	bool commit = input.GetAxis(InputAxis::ZAxis) != 0;
	bool removeCommit = input.GetAxis(InputAxis::WAxis) != 0;

	auto currentInput = Vector3(xAxisRaw > 0 ? 1 : xAxisRaw < 0 ? -1 : 0, yAxisRaw > 0 ? 1 : yAxisRaw < 0 ? -1 : 0, hue);
	if (currentInput.Z < 0)
	{
		currentInput += Vector3(0, 0, 360);
	}

	point += currentInput;

	if (commit && (commit != lastCommit))
	{
		lastLastPoint = Vector3((int)lastPoint.X, (int)lastPoint.Y, lastPoint.Z);
		lastPoint = Vector3((int)point.X, (int)point.Y, ((int)(point.Z+ 360) % 360) / 360.f);
		list.push_back(lastPoint);
	}

	//ctrl z
	if (removeCommit && (removeCommit != lastRCommit))
	{
		list.erase(list.end() - 1);
	}

	lastRCommit = removeCommit;
	lastCommit = commit;
}

// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
	// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& r = GetRenderer();
	const auto& g = Get2DGameEngine();

	// 배경에 격자 그리기
	DrawGizmo2D();
	
	// 메시 데이터의 선언
	static constexpr float squareHalfSize = 0.5f;
	auto vertexCount = list.size();

	if (vertexCount >= 3)
	{
		// 변환된 정점을 잇는 선 그리기
		for (size_t ti = 0; ti < vertexCount - 2; ++ti)
		{
			size_t t0 = ti;
			size_t t1 = ti + 1;
			size_t t2 = ti + 2;

			Vector2 tv0 = list[t0].ToVector2();
			Vector2 tv1 = list[t1].ToVector2();
			Vector2 tv2 = list[t2].ToVector2();

			Vector2 u = tv0 - tv2;
			Vector2 v = tv1 - tv2;

			float uDotv = u.Dot(v);
			float uDotu = u.Dot(u);
			float vDotv = v.Dot(v);

			float denominator = uDotv * uDotv - uDotu * vDotv;
			float invDenominator = 1.f / denominator;

			float maxX = Math::Max3(tv0.X, tv1.X, tv2.X);
			float maxY = Math::Max3(tv0.Y, tv1.Y, tv2.Y);
			float minX = Math::Min3(tv0.X, tv1.X, tv2.X);
			float minY = Math::Min3(tv0.Y, tv1.Y, tv2.Y);

			ScreenPoint minScreen(Vector2(minX, minY));
			ScreenPoint maxScreen(Vector2(maxX, maxY));

			for (int y = minScreen.Y; y <= maxScreen.Y; ++y)
			{
				for (int x = minScreen.X; x <= maxScreen.X; ++x)
				{
					Vector2 target(x, y);
					Vector2 w = target - tv2;

					float wDotu = w.Dot(u);
					float wDotv = w.Dot(v);

					float s = (wDotv * uDotv - wDotu * vDotv) * invDenominator;
					float t = (wDotu * uDotv - wDotv * uDotu) * invDenominator;

					float oneMinusST = 1.f - s - t;
					if ((s >= 0.f && s <= 1.f) && (t >= 0.f && t <= 1.f) && (oneMinusST >= 0.f && oneMinusST <= 1.f))
					{
						auto color = HSVColor(list[t0].Z, 0.5f, 0.9f).ToLinearColor() * s + HSVColor(list[t1].Z, 0.5f, 0.9f).ToLinearColor() * t + HSVColor(list[t2].Z, 0.5f, 0.9f).ToLinearColor() * oneMinusST;
						r.DrawPoint(ScreenPoint::ToScreenCoordinate(_ScreenSize, target), color);
					}
				}
			}
		}
	}

	for (int x = -5; x < 5; ++x)
	{
		for (int y = -5; y < 5; y++)
		{
			r.DrawPoint(ScreenPoint::ToScreenCoordinate(_ScreenSize, point.ToVector2() + Vector2(x, y)), LinearColor::Red);
			r.DrawPoint(ScreenPoint::ToScreenCoordinate(_ScreenSize, lastPoint.ToVector2() + Vector2(x, y)), LinearColor::Blue);
			r.DrawPoint(ScreenPoint::ToScreenCoordinate(_ScreenSize, lastLastPoint.ToVector2() + Vector2(x, y)), LinearColor::Green);
		}
	}

	// 현재 위치, 크기, 각도를 화면에 출력
	r.PushStatisticText(std::string("Position : ") + currentPosition.ToString());
	r.PushStatisticText(std::string("Scale : ") + std::to_string(currentScale));
	r.PushStatisticText(std::string("Degree : ") + std::to_string(currentDegree));
}

10. Convex, Line Clipping,Mesh

절단 - 코핸서덜랜드 라인클리핑 알고리즘

일직선상에 위치하지 않은 세 점의 아핀조합 결과

컨벡스 및 컨벡스 조합 (Convex & Convex Combination)

3차원 물체의 기본단위는 왜 삼각형?

트라이앵글 리스트 방법으로 메시를 표현하는 방법 정리

무게중심 좌표가 가지는 의미와 특징

내적을 사용해 삼각형과 같은 평면에 위치한 점의 무게중심 좌표계를 구하는 수식 정리

예제를 기반으로 메시를 설계하고 구현.

Further Reading

1. Number Structure

2. Function & Vector

3. Vector