1. 스크린 좌표계와 데카르트 좌표계가 가지는 차이점을 비교해 정리
수 집합(Field)
좌표계
성질
스크린 좌표계
양의 정수( )
왼손좌표계
이산성
데카르트 좌표계
실수( )
오른손좌표계
연속성
2. 픽셀화를 정의하고, 픽셀화를 위해 필요한 규칙을 정의하시오 ( 점 기준 )
픽셀화를 보통 Rasterization. 래스터화라고 합니다. 래스터가 무엇일까요?
래스터화에서 나오는 래스터 그래픽스는 비트맵 그래픽스라고 볼 수 있습니다.
개별적으로 제어되는 점에 의해 영상이나 이미지를 표시하는 방식이며, 수학에서 선과 모양을 표현하기 위한 방법입니다.
저희는 모니터의 화면을 구성하는 화소, 즉 픽셀을 기준으로 다루겠습니다.
래스터화에서, 물리적인 픽셀과 픽셀사이의 중간에 위치한 수학적 점을 생각해봅시다.
스크린크기가 홀수라면 0,0에 점을 찍을때는 width / 2, height / 2 로 하면 되지만, 스크린 크기가 짝수라면, 중심 비트맵 점을 정확히 표현할 수 없다는 단점이 있습니다.
둘 다 그리거나, 둘 다 안그리거나. 정할 수 없는 것이죠
이를 위해, 표현하는 방법을 정의합니다. 이를 Rasterization Rules 라고 합니다.
여러 예시를 들어봅시다. 아참, 이것은 화면 좌표계가 아닌 래스터화 규칙입니다.
- 좌상단 (Top-Left rule)
- Direct X
- OpenGL
- (windows) GDI
- 우하단(Bottom-Right rule)
- SoftRenderer (ㅎㅎ)
왼쪽 상단 채우기 규칙(Top-left Rule)
간단하게 설명한다면, 어느방향으로 검사를 진행하냐고 볼 수 있습니다.
좌상단 채우기 규칙은 간단히 말해 수학적 점의 위치에서 좌측과 상단의 변에 대응되는지로만 검사를 진행합니다. 우하단 규칙은 반대로 하단과 우측의 변에 대응되는지에 대한 검사만 진행합니다.
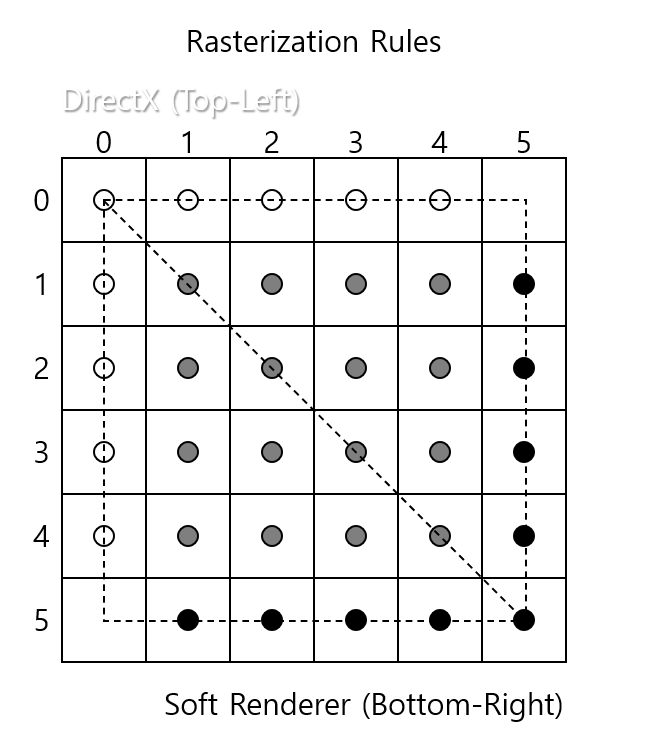
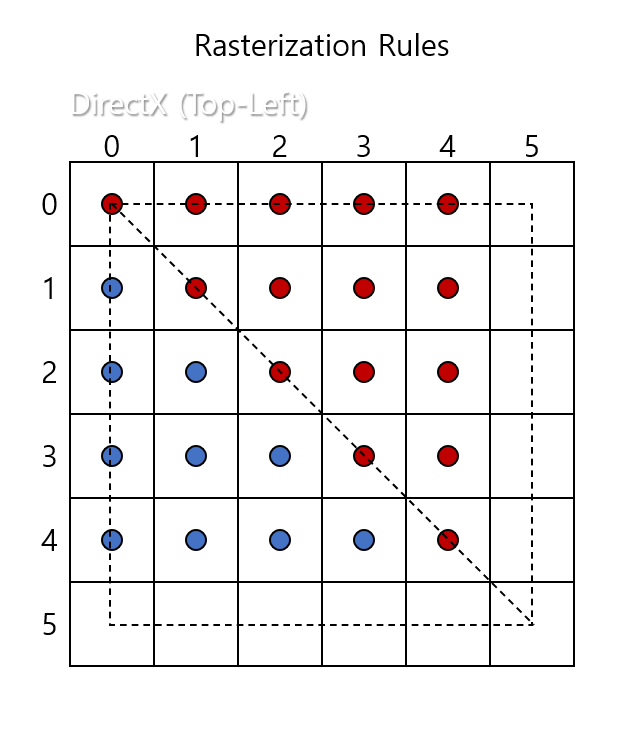
이는 연결된 두 삼각형의 경우, 자석의 N극과 S극처럼
한 삼각형의 이웃한 변이 왼쪽이라면 다른 삼각형에게서 그 변은 오른쪽이기 때문입니다.
따라서 중복되거나, 빈공간이 생기지 않고 꼼꼼하게 채울 수 있게 됩니다.
이를 수학적 점과 픽셀의 관계에 대해 사용할때는 다음과 같습니다.
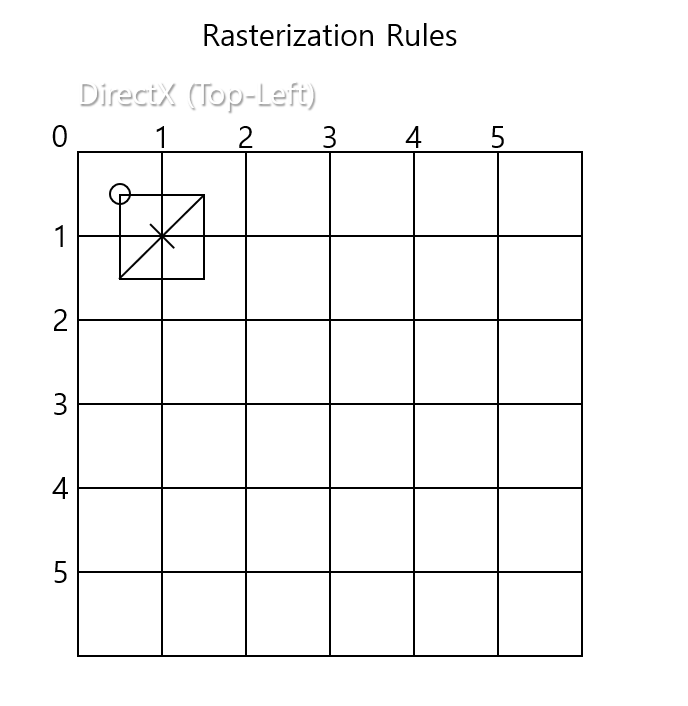
수학적 점에서 1*1 사이즈의 Z 패턴 사각형 을 그린 후 Top-Left filling convention을 적용하는 것입니다. 사이즈만 작을 뿐 동일하니까요.
- 아마 이것은 Top-Left filling convention 때문에 Z패턴을 사용하는 것 같습니다. 만약 Top-Right filling Convention이 절대적이였다면 저 위의 큰 네모와 같은 삼각형으로 구성된 사각형이겠죠?
3. 우하단을 사용하는 예제 프로그램의 픽셀화 규칙을 DirectX로 바꾸기 위해서는 아래 코드를 어떻게 바꿔야 하는가?
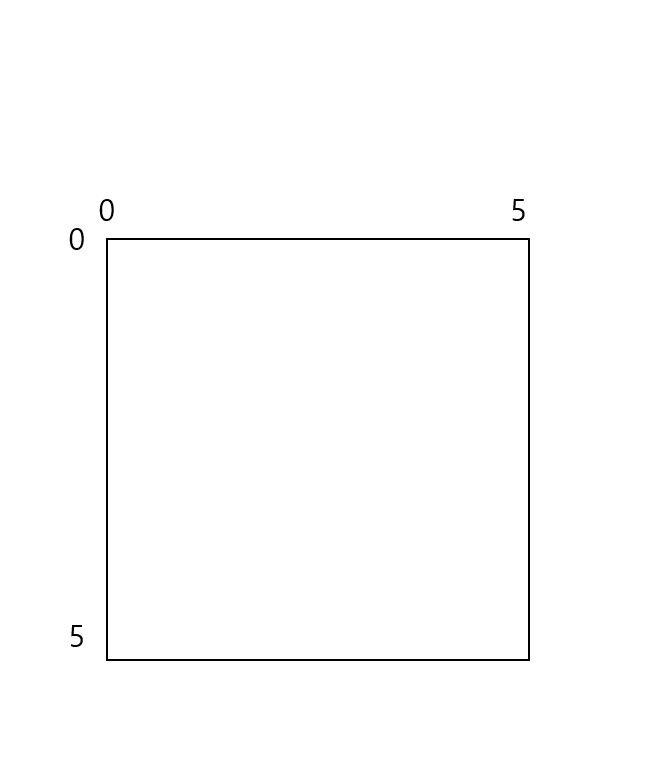
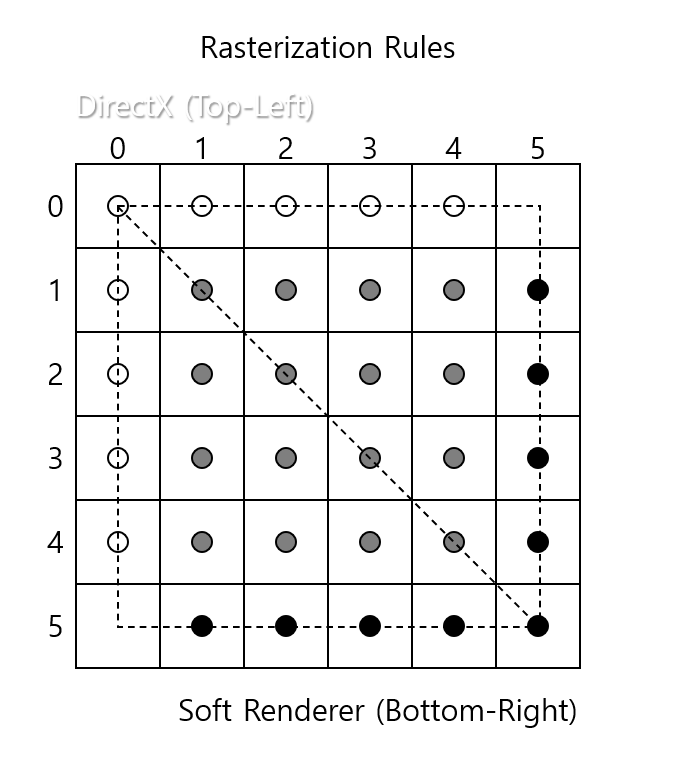
픽셀화 규칙(Rasterization Rules) 부터 확인하도록 합시다.
길이 5 높이 5의 사각형을 스크린 좌표 (0,0), (5,0) (0,5) (5,5)에 대응하였다고 가정을 합시다.
그러면 Top-Left룰에서는 0,0부터 4,4까지(흰색 및 회색)을,
Bottom-Right 룰에서는 1,1부터 5,5 까지를(회색 및 검정색)을 그리게 됩니다.
즉 두 규칙의 차이는 1이라는 크기의 차이가 납니다.
예제 프로그램의 코드를 확인해 봅시다.
1
2
3
4
5
6
7
8
9
10
//예제 프로그램
FORCEINLINE static constexpr ScreenPoint ToScreenCoordinate(const ScreenPoint& InScreenSize, const Vector2& InPos)
{
return ScreenPoint(InPos.X + InScreenSize.X * 0.5f, -InPos.Y + InScreenSize.Y * 0.5f);
}
FORCEINLINE constexpr Vector2 ToCartesianCoordinate(const ScreenPoint& InScreenSize)
{
return Vector2(X - InScreenSize.X * 0.5f + 0.5f, -(Y + 0.5f) + InScreenSize.Y * 0.5f);
}
여기서잠깐. ToScreenCoordinate을 잘 살펴봅시다.
화면길이가 4인 경우를 생각해봅시다. 그러면 절반값은 2가 되는데,
이걸 0~3에 대응해보면 0 1 [2] 3 입니다.
이유는 Floor연산을 하기 때문에,
좌표가 0보다 작아질 경우 -1로 넘어가고, 그러면 좌표값은 1이 됩니다.
하지만 이는 기본이 Bottom-Right일 경우입니다.
저희가 원하는것은 0~3에 대응하였을 때 기본값 0에 대하여 0 [1] 2 3 ,
좌표가 0보다 커질 경우(ex 0.1) 1이 늘어난 좌표값 2가 되어야합니다.
따라서 InScreenSize의 특정 성분 N에 대하여, N * 0.5가 아닌 (N * 0.5 - 1)의 값을 더해주며,
기존 좌표에 대해 Ceil처리를 해줍니다.
그리고 반대의 경우도 계산해줍니다.
이때, 기존에는 0으로 floor되었기 때문에 InScreenSize.X * 0.5f + 0.5f 를 진행하였다면
지금은 Ceil처리하기때문에 0.5를 빼주어야합니다.
결론적으로 다이렉트 X 라면 다음과 같이 코드를 작성할 것 같습니다.
원본코드는 비교하기 쉽도록 주석을 걸어두었습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//예제 프로그램
FORCEINLINE static constexpr ScreenPoint ToScreenCoordinate(const ScreenPoint& InScreenSize, const Vector2& InPos)
{
//return ScreenPoint(
// InPos.X + InScreenSize.X * 0.5f,
// -InPos.Y + InScreenSize.Y * 0.5f);
return ScreenPoint(
Math::CeilToInt(InPos.X + InScreenSize.X * 0.5f - 1),
Math::CeilToInt(-InPos.Y + InScreenSize.Y * 0.5f - 1));
}
FORCEINLINE constexpr Vector2 ToCartesianCoordinate(const ScreenPoint& InScreenSize)
{
//return Vector2(X - InScreenSize.X * 0.5f + 0.5f, -(Y + 0.5f) + InScreenSize.Y * 0.5f);
return Vector2(X - InScreenSize.X * 0.5f - 0.5f, -(Y - 0.5f) + InScreenSize.Y * 0.5f);
}
마법의 숫자 -0.5?
계속 0.5 0.5 하고있으니 재미있는게 기억났습니다.
DirectX에서 텍스처링시 마법의 숫자 -0.5에 관한 이야기인데요,
이 또한 스크린좌표계와 데카르트 좌표계의 차이때문에 발생하는 문제입니다.
와 과제마감 수업일 기준으로 딱 10주년이 되는 글이네요!
(그러나 그 날은 부처님이 오셨다고 합니다.)
*추가 코멘트 (2021.5.24) - 예전에 봤던 글입니다! 참고하기 좋은글이라 추가적으로 인용합니다
https://blog.daum.net/gamza-net/16
[브레젠험 알고리즘 (bresenham’s line algorithm]
코드는 최대한 일반화하여 간결하게 짜보시오.
선을 그리기 위한 성분은 전체 크기, 진행 방향, 기울기로 분리할 수 있습니다.
기존 수식대로 진행한다면 나누고 곱함에 있어 부호를 손실할 수 있어, 이걸 모두 나뉘어 기억합니다.
그렇게된다면, 단순하게 덧셈인지 뺄셈인지 신경쓰지 않고, 진행방향의 값만큼 더하거나 하는 형태로 가능합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename T>
int sign(const T& val) // 부호값 (-1,0,1)을 구하기 위한 함수
{
return (T(0) < val) - (val < T(0));
}
template<typename T>
void customSwap(T& a, T& b) // 스왑 함수
{
T Temp = a;
a = b;
b = Temp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
void WindowsRSI::DrawLine(const Vector2& InStartPos, const Vector2& InEndPos, const LinearColor& InColor)
{
Vector2 clippedStart = InStartPos;
Vector2 clippedEnd = InEndPos;
Vector2 screenExtend = Vector2(_ScreenSize.X, _ScreenSize.Y) * 0.5f;
Vector2 minScreen = -screenExtend;
Vector2 maxScreen = screenExtend;
if (!CohenSutherlandLineClip(clippedStart, clippedEnd, minScreen, maxScreen))
{
return;
}
ScreenPoint startPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedStart);
ScreenPoint endPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedEnd);
int width = endPosition.X - startPosition.X;
int height = endPosition.Y - startPosition.Y;
// 여기에 관련 코드를 구현하기.
if(width == 0 && height == 0)
return;
ScreenPoint currentPos = startPosition;
//크기(w,h)
ScreenPoint delta((float)abs(endPosition.X - startPosition.X), (float)abs(endPosition.Y - startPosition.Y));
//증감방향
const ScreenPoint dir(sign(endPosition.X - startPosition.X), sign(endPosition.Y - startPosition.Y));
//기울기가 1을 넘는가
const bool isOverOne = delta.Y > delta.X;
if (isOverOne)
{
customSwap(delta.X, delta.Y);
}
//초기점 출력
SetPixel(ScreenPoint(currentPos.X, currentPos.Y), InColor);
int checker = 2 * delta.Y - delta.X; //2h - w
//큰 값 기준으로 선찍기 진행 (건너뛰지않기위해)
for (int i = 0; i <= delta.X; ++i)
{
//아래로 내려가야하는지 체크
while (checker >= 0)
{
if (isOverOne)
currentPos.X += dir.X;
else
currentPos.Y += dir.Y;
checker -= 2 * delta.X; // -2w
}
//평행이동
if (isOverOne)
currentPos.Y += dir.Y;
else
currentPos.X += dir.X;
checker += 2 * delta.Y; // +2h
//출력
SetPixel(ScreenPoint(currentPos.X, currentPos.Y), InColor);
}
}
기울기에 따라 특정성분에 특정값을 넣는게 조금 코드일반화가 힘듭니다.
만약 색상곱 처럼 각 벡터의 곱을 넣을 수 있다면 다음과 같은형태로 바꿀 수 있었을 것 같습니다.
1
2
3
4
5
6
7
8
9
10
if (isOverOne) currentPos.X += dir.X;
else currentPos.Y += dir.Y;
//=>
currentPos += downMask * dir;
//평행이동
if (isOverOne) currentPos.Y += dir.Y;
else currentPos.X += dir.X;
//=>
currentPos += translationMask * dir;
예시프로젝트
어…버텍스 정보를 가져와서 그림을 그릴까 하다가 숫자 노가다하고 있는 절 보며…
이럴꺼면 직접 포인터를 이동해서 찍으면 되는거 아닌가? 하고 바꿨습니다
(GIF입니다. 실시간 드로잉 쇼)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void SoftRenderer::Update2D(float InDeltaSeconds)
{
auto& g = Get2DGameEngine();
const InputManager& input = g.GetInputManager();
const float HueShiftRate = 60.f;
auto xAxisRaw = input.GetAxis(InputAxis::XAxis) * InDeltaSeconds;
auto yAxisRaw = input.GetAxis(InputAxis::YAxis) * InDeltaSeconds;
auto hue = input.GetAxis(InputAxis::WAxis) * InDeltaSeconds * HueShiftRate;
bool commit = input.GetAxis(InputAxis::ZAxis) != 0;
auto currentInput = Vector3(xAxisRaw > 0 ? 1 : xAxisRaw < 0 ? -1 : 0, yAxisRaw > 0 ? 1 : yAxisRaw < 0 ? -1 : 0, hue);
if (currentInput.Z < 0)
{
currentInput += Vector3(0, 0, 360);
}
point += currentInput;
if (commit)
{
list.push_back(point);
}
}
// 렌더링 로직
void SoftRenderer::Render2D()
{
auto& r = GetRenderer();
const auto& g = Get2DGameEngine();
// 격자 그리기
DrawGrid2D();
if (!list.empty())
{
auto size = list.size();
for (int i = 0; i < size - 1; ++i)
{
r.DrawLine(list[i].ToVector2(), list[i + 1].ToVector2(), HSVColor(((list[i].Z * 0.5f + list[i + 1].Z * 0.5f) + 360) / 360.f, 0.5f, 0.9f).ToLinearColor());
}
}
r.DrawPoint(point.ToVector2(), HSVColor((point.Z + 360) / 360.f, 0.5f, 0.9f).ToLinearColor());
}
