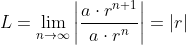Differentiation & Maclaurin’s series
머릿말
수업과 크리틱은 병실에서 듣겠습니다.
그래서 파워포인트가 없어서 그림을 못그립니다.
미분(Differentiation) 아 이거 단어를 좀 잘 봐야합니다
derivative와 differentiation이 있는데, 미분 하는건 diff고 이 값들의 집합은 derivative입니다.
상수 함수의 미분은 0이다. 이의 의미를 설명하시오. 상수함수가 무엇인지 부터 알아야겠죠?
f ( x ) = c y = c f(x)=c\\ y=c f ( x ) = c y = c 즉 다음과 같은 꼴을 말합니다.
저희가 변경사항을 찾아볼 때 보통 ‘diff 딴다’ 라는 말을 많이 하잖아요? (우리만 그런가..)
여기서 diff는 파일 비교 유틸리티인데, Differential(미분)라는 단어를 생각하면 또 맞습니다.
미분 - diff는 결국 변화를 표현한다고 보면 되죠.
그리고 상수함수에서는 이 매개변수(x)의 변화에 대한 변화량이 없습니다.
그러므로 상수함수의 미분은 0이 되는 것이죠.
수식적으로 들어간다면 다음과 같이 볼 수 있죠.
f ( x ) = c lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 c − c h = lim h → 0 0 h = 0 f(x)=c \\ \lim_{h\rightarrow0} \frac{f\left(x+h\right)-f \left(x \right)} {h}= \\ \lim_{h\rightarrow0} \frac{c-c}{h}= \\ \lim_{h\rightarrow0} \frac{0}{h}=0 f ( x ) = c h → 0 lim h f ( x + h ) − f ( x ) = h → 0 lim h c − c = h → 0 lim h 0 = 0 함수의 극한이 가지는 성질에 대해 정리하시오. 극한의 성질 1 : 두 함수 합의 극한값은 각 극한값의 합과 같음 lim x → a [ f ( x ) + g ( x ) ] = lim x → a f ( x ) + lim x → a g ( x ) \lim_{x\rightarrow a}\left[f\left(x\right)+g\left(x\right)\right]=\lim_{x\rightarrow a}f\left(x\right)+\lim_{x\rightarrow a}g\left(x\right) x → a lim [ f ( x ) + g ( x ) ] = x → a lim f ( x ) + x → a lim g ( x ) 극한의 성질 2 : 상수와 함수 곱의 극한값은 함수 극한값에 상수를 곱한 것과 같음 lim x → a c f ( x ) = c lim x → a f ( x ) \lim_{x\rightarrow a}{cf\left(x\right)}=c\lim_{x\rightarrow a}{f\left(x\right)} x → a lim c f ( x ) = c x → a lim f ( x ) 극한의 성질 3 : 두 함수 곱의 극한값은 각 극한값의 곱과 같음 lim x → a [ f ( x ) ⋅ g ( x ) ] = lim x → a f ( x ) ⋅ lim x → a g ( x ) \lim_{x\rightarrow a}\left[f\left(x\right)\cdot g\left(x\right)\right]=\lim_{x\rightarrow a}f\left(x\right)\cdot\lim_{x\rightarrow a}g\left(x\right) x → a lim [ f ( x ) ⋅ g ( x ) ] = x → a lim f ( x ) ⋅ x → a lim g ( x ) 극한의 성질 4 : 두 함수 나눗셈의 극한값은 각 극한값의 나눗셈과 동일 단 분모의 극한값은 0이 아니어야 한다.
lim x → a [ f ( x ) g ( x ) ] = lim x → a f ( x ) lim x → a g ( x ) \lim\limits_{x\rightarrow a}\left[\frac{f\left(x\right)}{g\left(x\right)}\right]=\frac{\lim\limits_{x\to a}{f\left(x\right)}}{\lim\limits_{x\to a}{g\left(x\right)}} x → a lim [ g ( x ) f ( x ) ] = x → a lim g ( x ) x → a lim f ( x ) 극한의 성질 5 : 함수를 거듭제곱한 극한값은 극한값을 거듭제곱한 값과 같음 lim x → a [ f ( x ) ] n = [ lim x → a f ( x ) ] n \lim_{x\rightarrow a}\left[f\left(x\right)\right]^n=\left[\lim_{x\rightarrow a}f\left(x\right)\right]^n x → a lim [ f ( x ) ] n = [ x → a lim f ( x ) ] n 극한의 성질 6 : 조임 정리, 샌드위치 정리(Squeeze Theorem) 세 함수의 대소 관계가 g ( x ) ≤ f ( x ) ≤ h ( x ) g\left(x\right)\le f\left(x\right)\le h\left(x\right) g ( x ) ≤ f ( x ) ≤ h ( x )
‘어떤 점에서’ 양변 g ( x ) g\left(x\right) g ( x ) h ( x ) h\left(x\right) h ( x ) f ( x ) f(x) f ( x )
lim x → a f ( x ) = L s . t . lim x → a g ( x ) = lim x → a h ( x ) = L \lim_{x\rightarrow a}f\left(x\right)=L \\ s.t. \lim_{x\rightarrow a}g\left(x\right)=\lim_{x\rightarrow a}h\left(x\right)=L x → a lim f ( x ) = L s . t . x → a lim g ( x ) = x → a lim h ( x ) = L 이 성질은 잘 생각하기 어려운데, 나중에 삼각함수의 미분을 할때 쓰게 되므로, 조금 더 가봅시다.
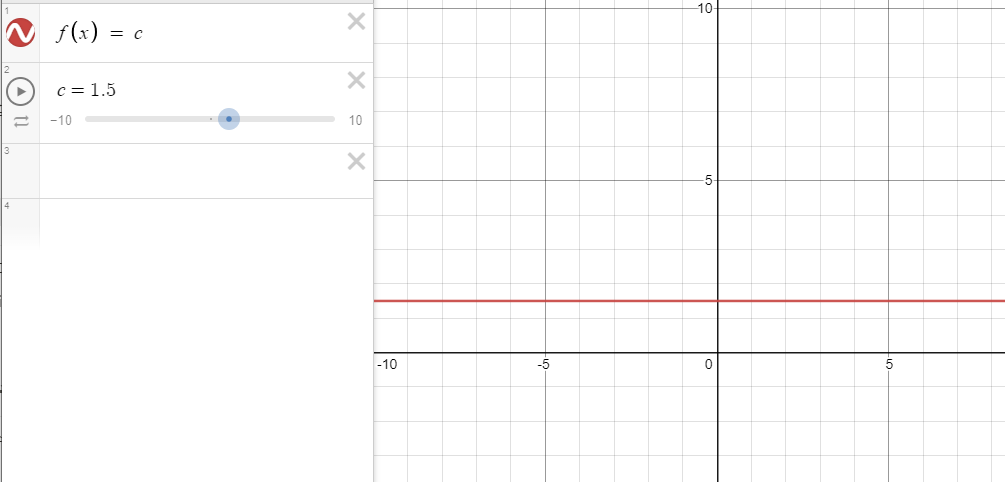
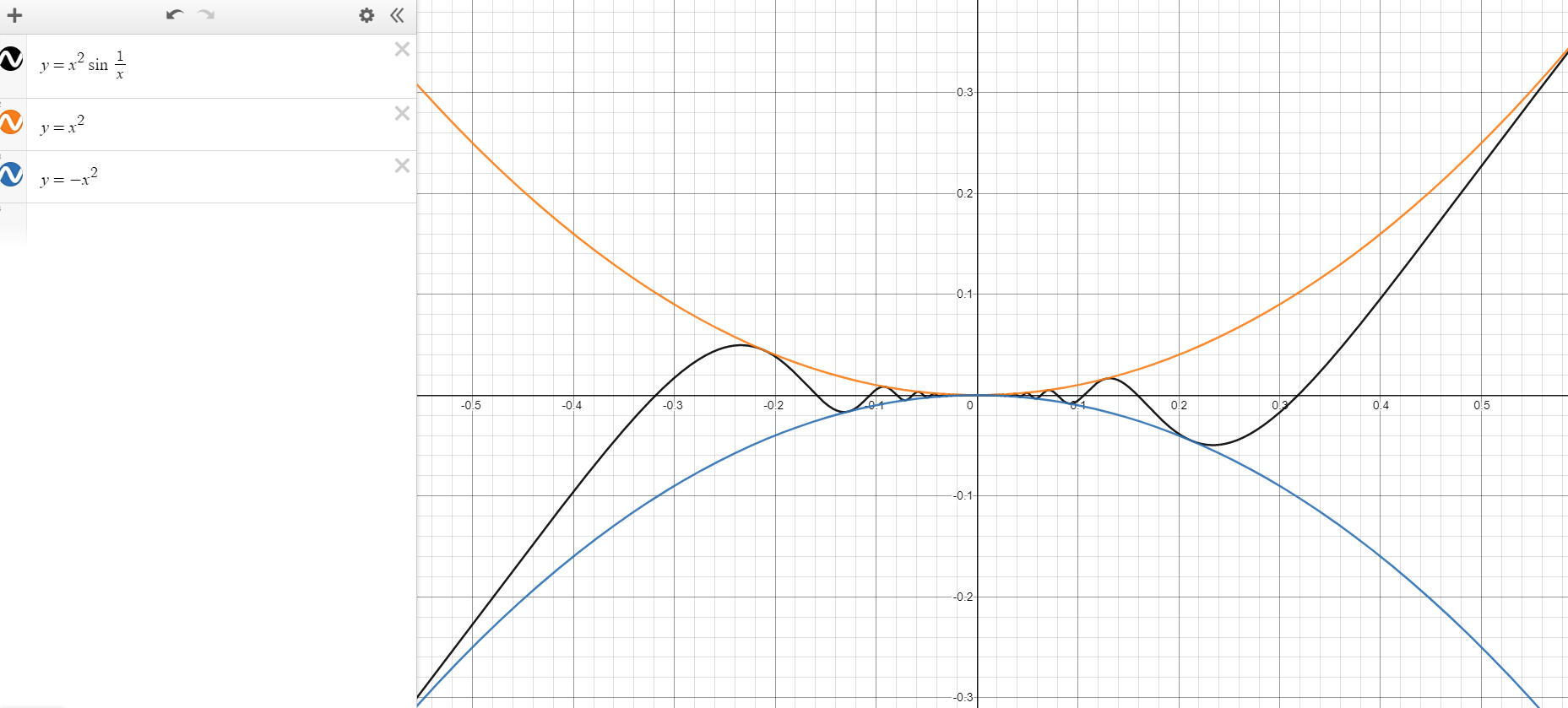
두 함수 사이를 진동하는 그래프의 예시를 하나 들어본다면
g ( x ) = − x 2 f ( x ) = x 2 s i n 1 x h ( x ) = x 2 g(x) = -x^2\\ f(x) = x^2sin\frac{1}{x}\\ h(x) = x^2 g ( x ) = − x 2 f ( x ) = x 2 s in x 1 h ( x ) = x 2
넋두리
처음 이 이론을 접했을 때, ‘어떤 점에서’라는 한정자가 없어서, 어 그러면
g ( x ) = − 1 f ( x ) = s i n ( x ) h ( x ) = 1 g(x) = -1\\ f(x) = sin(x)\\ h(x) = 1 g ( x ) = − 1 f ( x ) = s in ( x ) h ( x ) = 1 이 케이스에서 위아래의 두 식의 미분값은 언제나 0인데, 그러면 sin(x)의 미분이 항상 0이라고? 라는 뭔 이상한 케이스가 존재 하는가? 하면서 들었습니다. 하지만 정확히 이론을 조사해본 결과, 샌드위치, 조임정리는 두 함수가 한점에서 만날 때를 기준으로 설명합니다.
함수의 극한이 가지는 성질을 활용해 자연지수함수의 도함수를 구하시오. 자연지수함수의 도함수 f ( x ) = e x f ′ ( x ) = e x f(x)=e^x \\ f'(x)=e^x f ( x ) = e x f ′ ( x ) = e x f ′ ( x ) = lim h → 0 e x + h − e x h = lim h → 0 e x ⋅ e h − e x h = e x ⋅ lim h → 0 e h − 1 h 성질1에 의해 분리하면, 분자와 분모가 같으므로 = e x ⋅ 1 = e x f'(x) = \lim_{h\rightarrow 0} \frac{e^{x+h} - e^x}{h} \\ \space\\=\lim_{h\rightarrow 0} \frac{e^x\cdot e^h - e^x}{h} \\ \space\\ = e^x \cdot \lim_{h\rightarrow 0} \frac{e^h -1}{h} \\\space\text{성질1에 의해 분리하면, 분자와 분모가 같으므로}\\ = e^x \cdot 1\\ = e^x f ′ ( x ) = h → 0 lim h e x + h − e x = h → 0 lim h e x ⋅ e h − e x = e x ⋅ h → 0 lim h e h − 1 성질 1 에 의해 분리하면 , 분자와 분모가 같으므로 = e x ⋅ 1 = e x sin함수의 도함수를 구하시오. 구해야할 핵심 모듈은 다음식입니다. 빠르게 빠르게(입원 11시간 전) 작성해봅시다.
lim h → 0 s i n h h = 1 \lim_{h\rightarrow0}{\frac{sin{h}}{h}}=1 h → 0 lim h s in h = 1 원의 넓이 S = π ⋅ r 2 S=\pi\cdot r^2 S = π ⋅ r 2 반지름이 1인 부채꼴의 넓이 S c s 1 = 1 2 r ⋅ ( θ 360 2 π r ) ( d e g ) S c s 1 = θ 2 r 2 ( r a d ) S c s 1 = θ 2 ⋅ 1 2 S_{cs1} = \frac{1}{2}r\cdot(\frac{\theta}{360}2\pi r)(deg)\\ S_{cs1} = \frac{\theta}{2}r^2(rad)\\ S_{cs1}=\frac{\theta}{2}\cdot 1^2 S cs 1 = 2 1 r ⋅ ( 360 θ 2 π r ) ( d e g ) S cs 1 = 2 θ r 2 ( r a d ) S cs 1 = 2 θ ⋅ 1 2 반지름이 1인 부채꼴 내부에서 가장 큰 삼각형의 넓이 S t = s i n θ 2 S_{t}=\frac{sin\theta}{2} S t = 2 s in θ 삼각형의 내부에서 가장 큰 부채꼴의 넓이 S c s 2 = θ 2 ⋅ c o s 2 θ S_{cs2}=\frac{\theta}{2}\cdot cos^2\theta S cs 2 = 2 θ ⋅ co s 2 θ 조임정리를 통한 극한 도출 S c s 2 < S t < S c s 1 θ 2 ⋅ c o s 2 θ < s i n θ 2 < θ 2 ⋅ 1 2 c o s 2 θ < s i n θ θ < 1 lim h → 0 c o s 2 h < lim h → 0 s i n h h < lim h → 0 1 lim h → 0 c o s 2 h = lim h → 0 1 = 1 lim h → 0 s i n h h = 1 S_{cs2}<S_t<S_{cs1}\\\frac{\theta}{2}\cdot cos^2\theta<\frac{sin\theta}{2}<\frac{\theta}{2}\cdot 1^2\\cos^2\theta<\frac{sin\theta}{\theta}<1\\\lim_{h\rightarrow0}cos^2h<\lim_{h\rightarrow0}\frac{sinh}{h}<\lim_{h\rightarrow0}1\\\lim_{h\rightarrow0}cos^2h=\lim_{h\rightarrow0}1=1\\\lim_{h\rightarrow0}\frac{sinh}{h}=1 S cs 2 < S t < S cs 1 2 θ ⋅ co s 2 θ < 2 s in θ < 2 θ ⋅ 1 2 co s 2 θ < θ s in θ < 1 h → 0 lim co s 2 h < h → 0 lim h s inh < h → 0 lim 1 h → 0 lim co s 2 h = h → 0 lim 1 = 1 h → 0 lim h s inh = 1 sin함수의 도함수 f ( x ) = s i n x f ′ ( x ) = lim h → 0 s i n ( x + h ) − s i n x h f ′ ( x ) = lim h → 0 s i n x c o s h + c o s x s i n h − s i n x h f ′ ( x ) = s i n x lim h → 0 ( c o s h − 1 ) h + c o s x lim h → 0 s i n h h f ′ ( x ) = s i n x ⋅ 0 + c o s x ⋅ 1 f ′ ( x ) = c o s x f(x)=sinx\\f'(x)=\lim_{h\rightarrow0}\frac{sin(x+h)-sinx}{h}\\f'(x)=\lim_{h\rightarrow0}\frac{sinxcosh+cosxsinh-sinx}{h}\\f'(x)=sinx\lim_{h\rightarrow0}\frac{(cosh-1)}{h}+cosx\lim_{h\rightarrow0}\frac{sinh}{h}\\f'(x)=sinx\cdot0+cosx\cdot1\\f'(x)=cosx f ( x ) = s in x f ′ ( x ) = h → 0 lim h s in ( x + h ) − s in x f ′ ( x ) = h → 0 lim h s in x cos h + cos x s inh − s in x f ′ ( x ) = s in x h → 0 lim h ( cos h − 1 ) + cos x h → 0 lim h s inh f ′ ( x ) = s in x ⋅ 0 + cos x ⋅ 1 f ′ ( x ) = cos x f ( x ) = s i n ( x ) , f ′ ( x ) = c o s ( x ) f(x) = sin(x), f'(x) = cos(x) f ( x ) = s in ( x ) , f ′ ( x ) = cos ( x ) cos함수의 도함수를 구하시오. cos함수의 도함수 f ( x ) = c o s x f ′ ( x ) = lim h → 0 c o s ( x + h ) − c o s x h f ′ ( x ) = lim h → 0 c o s x c o s h − s i n x s i n h − c o s x h f ′ ( x ) = c o s x lim h → 0 c o s h − 1 h − s i n x lim h → 0 s i n h h f ′ ( x ) = c o s x ⋅ 0 − s i n x ⋅ 1 f ′ ( x ) = − s i n x f(x)=cosx\\f'(x)=\lim_{h\rightarrow0}\frac{cos(x+h)-cosx}{h}\\f'(x)=\lim_{h\rightarrow0}\frac{cosxcosh-sinxsinh-cosx}{h}\\f'(x)=cosx\lim_{h\rightarrow0}\frac{cosh-1}{h}-sinx\lim_{h\rightarrow0}\frac{sinh}{h}\\f'(x)=cosx\cdot0-sinx\cdot1\\f'(x)=-sinx f ( x ) = cos x f ′ ( x ) = h → 0 lim h cos ( x + h ) − cos x f ′ ( x ) = h → 0 lim h cos x cos h − s in x s inh − cos x f ′ ( x ) = cos x h → 0 lim h cos h − 1 − s in x h → 0 lim h s inh f ′ ( x ) = cos x ⋅ 0 − s in x ⋅ 1 f ′ ( x ) = − s in x f ( x ) = c o s ( x ) , f ′ ( x ) = − s i n ( x ) f(x) = cos(x), f'(x) = -sin(x) f ( x ) = cos ( x ) , f ′ ( x ) = − s in ( x ) 매클로린 급수(Maclaurin’s series) 여기부분 재미있습니다.
Unity의 버스트 컴파일러는 정확도를 희생하여 최적화를 수행하는(accuracy sacrificing optimization) 가능한데, 이게 유추하기론 테일러급수를 통한 최적화일 가능성이 있다는 것이죠.
유니티 DOTS 문서 발췌 https://blog.unity.com/kr/technology/on-dots-c-c 아, 그거아시나요? mathemetics가 아니라 mathematics 입니다.
그 테일러 급수의 부분집합이 바로 매클로린 급수입니다.
등비수열의 정의와 등비수열을 구성하는 요소를 나열하고 n번째 항을 표현하시오 등비수열(Geometric Sequence) 일정한 비를 가지는 수열을 의미합니다.
초항(First term) : a 공비,등비 (Common Ratio) : r 점화식 : a n = a r n − 1 a_n = a r^{n-1} a n = a r n − 1 일반항 : a n = a r n − 1 a_n = a r^{n-1} a n = a r n − 1 등비급수의 정의와 등비급수가 수렴할 때의 조건과 그 값을 구하시오. 등비급수(Geometric Series) 각 항 간의 비가 일정한 급수를 말합니다. 앞의 항에 일정한 수를 곱하여 다음 항이 됩니다.
등비급수가 수렴할 때의 조건과 그 값 s n = a + a r + a r 2 + a r 3 + ⋯ + a r n − 1 r s n = a r + a r 2 + a r 3 + a r 4 + ⋯ + a r n s n − r s n = a − a r n s n ( 1 − r ) = a ( 1 − r n ) s n = a ( 1 − r n ) 1 − r lim n → ∞ s n = lim n → ∞ a ( 1 − r n ) 1 − r lim n → ∞ s n = lim n → ∞ ( a 1 − r − a r n 1 − r ) lim n → ∞ s n = a 1 − r − a 1 − r ⋅ lim n → ∞ r n s_n=a+ar+ar^2+ar^3+\cdots+ar^{n-1}\\rs_n=ar+ar^2+ar^3+ar^4+\cdots+ar^n\\\space\\s_n-rs_n=a-ar^n\\s_n(1-r)=a(1-r^n)\\s_n=\frac{a(1-r^n)}{1-r}\\\space\\\lim_{n\rightarrow\infty}s_n=\lim_{n\rightarrow\infty}\frac{a(1-r^n)}{1-r}\\\lim_{n\rightarrow\infty}s_n=\lim_{n\rightarrow\infty}(\frac{a}{1-r}-\frac{ar^n}{1-r})\\\lim_{n\rightarrow\infty}s_n=\frac{a}{1-r}-\frac{a}{1-r}\cdot\lim_{n\rightarrow\infty}r^n s n = a + a r + a r 2 + a r 3 + ⋯ + a r n − 1 r s n = a r + a r 2 + a r 3 + a r 4 + ⋯ + a r n s n − r s n = a − a r n s n ( 1 − r ) = a ( 1 − r n ) s n = 1 − r a ( 1 − r n ) n → ∞ lim s n = n → ∞ lim 1 − r a ( 1 − r n ) n → ∞ lim s n = n → ∞ lim ( 1 − r a − 1 − r a r n ) n → ∞ lim s n = 1 − r a − 1 − r a ⋅ n → ∞ lim r n 해당식의 실질적 의미를 가지는 공비, r의 값을 살펴보면
r = 1 r=1 r = 1 ∣ r ∣ > 1 \vert r\vert >1 ∣ r ∣ > 1 ∣ r ∣ < 1 \vert r\vert <1 ∣ r ∣ < 1 r = − 1 r=-1 r = − 1 따라서 수렴할때의 조건은
멱급수의 정의와 멱급수가 수렴함을 판정하기 위한 비판정법에 대해 정리하시오. 멱 급수(Power Series) 각 항들이 x n x^n x n
f ( x ) = ∑ n = 0 ∞ c n x n = c 0 + c 1 x + c 2 x 2 + ⋅ ⋅ ⋅ + c n x n + ⋅ ⋅ ⋅ f(x) = \sum_{n=0}^{\infin}c_nx^n = c_0+c_1x+c_2x^2+\cdot\cdot\cdot+c_nx^n + \cdot\cdot\cdot f ( x ) = n = 0 ∑ ∞ c n x n = c 0 + c 1 x + c 2 x 2 + ⋅ ⋅ ⋅ + c n x n + ⋅ ⋅ ⋅ c n c_n c n x x x 비판정법(비율판정법, ratio test) 이름을 보면 느낄 수 있죠? 변화의 비율을 보며 수렴인지 발산인지 판정하는 방법입니다.
L = lim n → ∞ ∣ a n + 1 a n ∣ L=\lim_{n\rightarrow\infty}\space \vert \frac{a_{n+1}}{a_n}\vert L = n → ∞ lim ∣ a n a n + 1 ∣ 해당 값이 나올 수 있는 케이스에 대해
L < 1 L<1 L < 1 L > 1 L>1 L > 1 L = 1 L=1 L = 1 입니다.
비판정법을 사용해 멱급수의 일종인 등비급수가 수렴하기 위한 조건을 정리하시오. 등비급수에서 비판정법을 나타내볼까요?
L = lim n → ∞ ∣ a ⋅ r n + 1 a ⋅ r n ∣ = ∣ r ∣ L=\lim_{n\rightarrow\infin} \bigg\vert \frac{a\cdot r^{n+1}}{a\cdot r^n}\bigg\vert = \vert r\vert L = n → ∞ lim a ⋅ r n a ⋅ r n + 1 = ∣ r ∣ frac과 \bigg \vert 이 좀 문제네요.
아 그거아시나요? https://latex.codecogs.com/png.latex ? 를 통해 이미지를 구해올 수 있습니다.
수렴조건은 비판정법과 같습니다. 이를 정리하면,
L < 1 = ∣ r ∣ < 1 L<1\quad=\quad\vert r\vert <1 L < 1 = ∣ r ∣ < 1 입니다.
어떤 함수가 멱급수로 표현가능하다고 가정했을 때 멱급수를 구성하는 각 계수의 값이 가지는 규칙을 정리하시오. f ( x ) = ∑ n = 0 ∞ c n x n = c 0 + c 1 x + c 2 x 2 + ⋅ ⋅ ⋅ + c n x n + ⋅ ⋅ ⋅ f(x) = \sum_{n=0}^{\infin}c_nx^n = c_0+c_1x+c_2x^2+\cdot\cdot\cdot+c_nx^n + \cdot\cdot\cdot f ( x ) = n = 0 ∑ ∞ c n x n = c 0 + c 1 x + c 2 x 2 + ⋅ ⋅ ⋅ + c n x n + ⋅ ⋅ ⋅ 위와 같은 멱급수를 매번 미분한다면 다음과 같이 표현할 수 있습니다.
f ( x ) = c 0 + c 1 ⋅ x + c 2 ⋅ x 2 + c 3 ⋅ x 3 + ⋯ f ′ ( x ) = 1 ⋅ c 1 + 2 ⋅ c 2 ⋅ x 1 + 3 ⋅ c 3 ⋅ x 2 + ⋯ f ′ ′ ( x ) = 1 ⋅ 2 ⋅ c 2 + 2 ⋅ 3 ⋅ c 3 ⋅ x 1 + ⋯ f(x) = c_0+c_1\cdot x+c_2\cdot x^2+c_3\cdot x^3 +\cdots \\ f'(x) = 1\cdot c_1 + 2\cdot c_2\cdot x^1 + 3\cdot c_3\cdot x^2 +\cdots\\ f''(x) = 1\cdot 2\cdot c_2+ 2\cdot 3\cdot c_3\cdot x^1 +\cdots f ( x ) = c 0 + c 1 ⋅ x + c 2 ⋅ x 2 + c 3 ⋅ x 3 + ⋯ f ′ ( x ) = 1 ⋅ c 1 + 2 ⋅ c 2 ⋅ x 1 + 3 ⋅ c 3 ⋅ x 2 + ⋯ f ′′ ( x ) = 1 ⋅ 2 ⋅ c 2 + 2 ⋅ 3 ⋅ c 3 ⋅ x 1 + ⋯ 어라? 계수부에 재미있는게 보이죠? 미분할때마다 규칙성이 보여요!
이제 0을 대입해 봅시다.
f ( 0 ) = c 0 = 0 ! ⋅ c 0 f ′ ( 0 ) = 1 ⋅ c 1 = 1 ! ⋅ c 1 f ′ ′ ( 0 ) = 1 ⋅ 2 ⋅ c 2 = 2 ! ⋅ c 2 f(0) = c_0 = 0! \cdot c_0\\ f'(0) = 1\cdot c_1 = 1! \cdot c_1\\ f''(0) = 1\cdot 2\cdot c_2= 2! \cdot c_2\\ f ( 0 ) = c 0 = 0 ! ⋅ c 0 f ′ ( 0 ) = 1 ⋅ c 1 = 1 ! ⋅ c 1 f ′′ ( 0 ) = 1 ⋅ 2 ⋅ c 2 = 2 ! ⋅ c 2 이렇게 여러번 미분한 도함수를 n계 도함수(n th derivative)라고 말하는데,
f ( n ) = f ′ ′ ⋯ ′ f^{(n)} = f^{''\cdots'} f ( n ) = f ′′ ⋯ ′ 로 표기합니다.
그렇다면 계수의 값은
c n = f ( n ) ( 0 ) n ! c_n = \frac{f^{(n)}(0)}{n!} c n = n ! f ( n ) ( 0 ) 라고 볼 수 있죠.
자연지수함수는 멱급수로 표현이 가능한가? 왜 그런지 그 이유를 설명하시오. 자연지수함수의 멱급수 표현은 다음과 같습니다.
e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋅ ⋅ ⋅ = ∑ n = 0 ∞ x n n ! e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+ \cdot\cdot\cdot =\sum_{n=0}^{\infin}\frac{x^n}{n!} e x = 1 + x + 2 ! x 2 + 3 ! x 3 + 4 ! x 4 + ⋅ ⋅ ⋅ = n = 0 ∑ ∞ n ! x n 왜냐하면, 비판정법에 의거해
L = lim n → ∞ x n + 1 ( n + 1 ) ! x n n ! = lim n → ∞ x n + 1 ∴ L < 1 L=\lim_{n\to\infty}\frac{\frac{x^{n+1}}{(n+1)!}}{\frac{x^n}{n!}} =\lim_{n\to\infty}\frac{x}{n+1}\\ \therefore L<1 L = n → ∞ lim n ! x n ( n + 1 )! x n + 1 = n → ∞ lim n + 1 x ∴ L < 1 수렴함이 증명되기 때문입니다.
맺음말 입원까지 7시간13분전, 수학과제 완료.

 아, 그거아시나요? mathemetics가 아니라 mathematics 입니다.](https://ashuatz.github.io/assets/10%20Differentiation%20&%20Maclaurin's%20series%2079b80499e98d428fa23aadb1ec9739fe/Untitled%203.png)