정의(Definition) 명제(Proposition) 공리(Axiom)
정의란 무엇인가
그것은 마이클 샌델의 책 제목입니다.
해당 책을 읽고나면 ‘마이클 샌델은 정의(justice)를 정의(define)하지 않았다.’ 라는 농담을 하곤 합니다.
정의(Definition)는 ‘이해함에 착오가 생기지 않도록 의미를 분명하게 설명한 문장’ 입니다.
예를 들어 를 ‘그 뭐냐 초등학교때 3.14 곱하던거’ 라고 하지 않고 ‘원의 둘레를 지름으로 나눈 값’ 이라고 설명하는 것이 정의입니다. 그리고 그 ‘정의한다’ 라는 것을 저는 정보의 탄생이라고 생각합니다. 아무것도 없는 세상에 정의를 내림으로써 무언가 생성되는 것이죠.
정의를 내림으로써 무언가를 만들었다면, 사용할 일이 있어야겠죠.
질문을 해봅시다. 다만 정의란 무엇인가? 라고 물으면 안됩니다.
‘참’ 혹은 ‘거짓’으로 결과가 나올 수 있어야합니다.
그렇게 해서 참과 거짓인 답을 판별할 수 있는 문장을 명제(Proposition)라고 합니다.
그런데 만약, ‘두 점이 있을때 두 점을 지나는 직선을 그을 수 있다’ 같은 누가봐도 답이 당연한 명제를 볼 경우가 있습니다. 이런 증명할 필요가 없는. 혹은 기초적인 근거가 되는 명제를 공리라고 합니다.
코드로 설명을 해보죠
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int temp = 10;
// 정의입니다 temp는 정수이며, 10의 값을 가지고 있다는 뜻이죠.
var proposition = (t) => t > 5;
// 명제입니다. t에 대해, t의 값이 5보다 크다는 명제를 정의하였습니다.
if(proposition(temp))
{
//temp는 5보다 크기때문에 참입니다.
//따라서 해당 위치에 접근하게 됩니다
}
else
{
//다만 temp가 10이 아닌 다른값으로 정의된다면, 해당 proposition은 거짓이 되겠죠.
//그 때, 이 위치로 접근하게 됩니다.
}
int temp2 = temp;
//temp2는 temp의 값을 갖습니다.
if(temp + 5 == temp2 + 5)
{
//공리입니다.
//temp와 temp2의 값은 같으니, 두 요소에 모두 5를 더한들 동일한것은 마찬가지겠죠.
}
else
{
//해당명제는 항상 참인 공리이기 때문에
//이 위치는 절대 접근할 일이 없습니다.
//이 위치에 접근할 일이 생긴다면, 현 수학의 근본이 뒤틀리게되겠죠
}
정리
공리 : 가장 기초적인 근거가 되는 증명할 필요가 없는 자명한 문제
명제 : 참을 판별할 수 있는 뜻이 분명한 문장
정의 : 용어의 의미를 분명하게 설명한 문장
수 집합의 종류와 기호
수 집합은 보통 칠판볼드체(세로에 가까운 선들을 두겹으로 사용)로 작성합니다.
고등학교때 이것에 관련된 일화가 있었는데, 여백이 부족해서 적지 않겠습니다.
: Natural number - 자연수의 집합
: integer (독어 Zahlen) - 정수의 집합
: rational number (독어 Quotient) - 유리수의 집합
: Real number - 실수의 집합
: Complex number - 복소수의 집합
…
: Hamilton number(quaternion) - 사원수(쿼터니언)
이항연산의 정의
이항연산이란 두 개의 항 사이에 이루어지는 연산입니다.
프로그래밍 함수정의에서 두 개의 인자와 하나의 반환값을 가진 연산이죠.
의 경우, 세 개의 항 사이에 연산이 이루어지는 것 같지만
이후 를 진행하기 때문에 이항연산입니다.
1
2
3
4
5
6
7
int add(in int a, in int b)
{
return a + b;
}
// a + b + c
var v = add(add(a + b),c);
후위표기법으로 계산기를 구현해 보았다면, 어떤 느낌인지 이해하실 수 있다고 생각합니다.
이항연산의 성질
가 비어있지 않은 집합이고, 및 가 에 대한 이진연산이라 가정합니다.
또한 이항연산은 항상 집합상에서만 이루어진다는 전제 조건이 주어집니다.
따라서 집합 내의 원소 를 추출하여 이항연산을 한다면, 그 결과가 에 속합니다.
Closure : 인 경우,
에 대한 연산 에 대해 닫혀있습니다.
- Commutative (교환) :
- Associative (결합) :
- Distributive (분배) :
Identity (항등원) : 요소 는 인 경우 는 모든 원소 에 대한 항등원입니다.
만약 이진연산이 (더하기)일 경우 이며, 이진연산이 (곱,)일 경우 입니다.
- Inverse (역원) : 요소 에 대해 연산 을 취하였을때 항등원 를 만드는 원소 입니다. 만약 이진연산이 (더하기)일 경우 이며, 이진연산이 (곱,)일 경우 입니다.
아마 아래 내용들을 읽다보면 이곳을 자주 볼겁니다.
수 집합이 다른 집합과 구분되는 특징
라고 한다면 수집합이 왜 나타나게 되었는가 부터 생각을 해봐야합니다.
수 집합은 대수학에서 사용되는데, 大(큰 대)가 아닌 代(대신할 대)입니다.
보통 이런걸 하는 이유는 프로그래밍에서도 자주 볼 수 있죠.
하나하나 처리할 수 없으니 유형을 세분화하여 정리하고,
유형별 집합이 확실하게 정의되었다면 추상화를 통해
유형별로 처리가 가능하기 때문입니다.
수 집합은 처리하기 위해 특성의 체계를 이룬것입니다.
거기서 발전하여 원소의 집합 뿐만이 아닌 연산을 함께 묶어낸 것이 대수적 체계(Algebraic System)입니다.
즉 기능과 데이터를 분리하다가, 하나로 묶은 클래스가 등장한 것이죠.
다시 본론으로 돌아와서, 이쯤되면 자꾸 나오는 단어인 ‘연산’을 행할 수 있다는게 수 집합과 다른 집합의 차이입니다.
그리고 이렇게 집합위에 연산이 행해지는 구조를 대수적 구조(Algebraic Structure)라고 합니다.
그게 바로 저희가 이제부터 알아볼 대상입니다.
크게 대수적 구조를 갖는 집합은 군(Group), 환(Ring), 체(Field) 등으로 쉽게 접근할 수 있는데,
여기서 군은 1개의 이항연산을, 환과 체는 2개의 이항연산을 갖게 됩니다.
어라 뭔가 이상하지 않나요? 사칙연산은 4개가 아닌가요?
사칙연산에서 뺄셈과 나눗셈을 사용하지 않아도 되는 이유
환과 체는 2개의 이항연산을 갖는다고 하였습니다.
그리고 그 이항연산은 제목에서 추론가능하듯, 덧셈()과 곱셈( )입니다.
생각해보면 단순합니다.
게임내에서 수수료 계산을 할 때 5%의 수수료를 제하여 받게될 때, 수신자가 정확히 N원을 받아야할 때가 있습니다. 이런 경우 저희는 받을금액의 0.95를 나눈 값을 지불합니다.
(대충 105,263,158원을 교환하면 100,000,000원을 수령합니다)
눈치채셨나요?
뺄셈은 역원(inverse)을 통해 덧셈으로( ),
나눗셈은 역원(inverse)을 통해 곱셈으로( ) 나타낼 수 있습니다.
다만 곱셈의 역원이 존재하는 수 체계 안에서의 이야기겠죠.
곱셈의 역원이 존재하지 않는다면 처리할 수 없으니까요.
곱셈의 역원이 존재하는 수 체계는 무엇일까요?
나눗셈 환(Division Ring)입니다. 뭐냐고요? 거의 체(Field)에 근접한 친구예요
나눗셈 환(Division Ring)에서 교환법칙(Commutativity)만 적용된다면 체(Field)입니다.
근데 저희가 평범하게 생각할때 일상생활에서 교환법칙이 안되는 곱은 없죠? (뭐라고요? 행렬 벡터 사원수라고요? 잘 못들었습니다?)
어쨋든 그러니 체(Field)를 알아봅시다.
체 구조를 구성하는 공리 정리
일단 체 공리(Field Axiom)부터 확인을 해볼까요?
- 덧셈 연산()에 대해
- 닫혀 있음(closure) - 군(Group) , 환(Ring) 집합 내 원소의 연산결과가 다시 그 집합 내에 존재
- 항등원(identity) 이 존재 ( ) - 군(Group), 환(Ring)
- 역원(inverse)이 존재 - 군(Group), 환(Ring)
- 결합법칙(associativity) 성립 - 군(Group), 환(Ring)
- 교환법칙(commutativity) 성립 - 가환군(Communtative Group), 환(Ring)
- 곱셈연산( )에 대해
- 닫혀 있음(closure) - 군(Group), 환(Ring) 집합 내 원소의 연산결과가 다시 그 집합 내에 존재
- 항등원(identity) 이 존재 ( ) - 군(Group)
- 0 이외의 모든 원소에서 역원(inverse)이 존재 - 군(Group)
- 0 이외의 모든 원소에서 결합법칙(associativity) 성립 - 군(Group), 환(Ring)
- 0 이외의 모든 원소에서 교환법칙(commutativity) 성립 - 가환환(Communtative Ring)
- 덧셈() 및 곱셈( )에 대해
- 덧셈에 대한 곱셈 연산의 분배법칙(distributivity) 성립 - 환(Ring)
즉 군(Group)은 모든 이항연산조건의 베이스이며,
환(Ring)은 군(Group)중
- 덧셈에 대해 ‘교환법칙이 성립하는 ‘가환군(Communtative Group)’ 특성’이 일치하고
- 곱셈에 대해 결합법칙이 성립하며,
- 덧셈과 곱셈에 대한 분배법칙이 성립한다.
체(Field)는
- 곱셈의 교환법칙이 성립하는 ‘가환환(Communtative Ring)’ 이며
- 곱셈의 항등원을 필요로하는 ‘단위환(Ring With Unity)’ 이며
- 동시에 곱셈의 역원이 존재해야한다.
여기서 곱셈의 항등원을 필요로하는 ‘단위환’ 에 곱셈의 역원이 존재하게 된다면
이걸 나눗셈환(Division Ring)이라고 합니다.
즉 체(Field)를 다시 설명하자면,
- 가환환(Communtative Ring)인 동시에 나눗셈환(Division Ring)
라고 설명할 수 있죠.
…
한국어는 너무어렵습니다.
특히 수학적인 무언가를 설명하는게 너무 어렵습니다.
위의 내용에서 더욱 정확한 조건을 넣어 정의를 내려야하지만 간단하게 설명드렸습니다.
이제 제가 이해한 방식을 상속으로 설명해보려합니다.
왜냐하면 저희는 어떤 것에서 어떤 조건을 만족하는게 어떤것이다. 라는 정의를 구성하는 것을 항상 해왔기 때문이죠.
코드작성을 멈춘지 좀 되어서 잘 기억이 안나지만, 대충 간략하게 구조를 나타내면
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//군
class Group<T> :
IClosure<T>,
IExistIdentity<T>,
IExistInverse<T>,
IAssociative<T>
where T : BinaryOperator{}
//가환군
class CommuntativeGroup<T> :
Group<T>,
ICommuntative<T>
where T : BinaryOperator{}
//환
class Ring :
CommuntativeGroup<Addition>,
IAssociative<Multiply>,
IDistributive<Addition,Multiply>{}
//가환환
class CommuntativeRing :
Ring,
ICommuntative<Multiply>{}
//단위원을 갖는 환, 단위환
class RingWithUnity :
Ring,
IExistIdentity<Multiply>{}
//나눗셈환
class DivisionRing:
RingWithUnity,
IExistInverse<Multiply>{}
//체
//CommuntativeRing(가환환) + DivisionRing(나눗셈환)
class Field :
Ring,
ICommuntative<Multiply>,
IExistIdentity<Multiply>,
IExistInverse<Multiply>{}
라고 이해하고 있습니다.
아, 방금 코드로 작성하며 느낀게 수학과 한국어로 읽히기 쉽게 작성하기 어려운 조건들이
제네릭과 상속, 인터페이스를 통해 쉽게 읽히도록 작성할 수 있다는 것입니다.
역시 프로그래밍 언어는 하나의 언어인가 봅니다.
아무튼 다시 돌아와서, 여기서 본 체(Field)는 수 체계 중 조건이 까다롭습니다.
다른말로 하자면 체에 속한 집합은 조건을 충족하기때문에 비교적 안정적이라 이리저리 굴리기 좋다는 뜻이 됩니다.
그런데 이 체에서 더 조건이 추가되거나 할 수 있습니다.
기본적으로 수 체계에서 사용하는 몇몇 집합은 원소가 무한하지만, 유한한 집합역시 존재할 수 있죠.
이를 유한체 혹은 갈로이스, 갈루아 체라고 합니다.
유한 / 갈루아 체(Finite Field / Galois Field)?
아까 field에서 범위가 정해지거나 셀 수 있다면 유한체 혹은 갈루아 체 라고 하였습니다.
유한하다. 즉 수량이 제한된 유한체의 표기는 , ,, 이라고 표현합니다.
여기서
- 를 위수 (Order), 유한 체 내 원소의 갯수(0포함)
- 를 표수(Characteristic)
라고 읽습니다.
유한체(Finite Field)는 체(Field)이며, 체(Field)는 곱셈의 역원이 존재해야 합니다.
유한체에서는 만약 가 소수이고 0 ~ 의 범위를 가진 정수집합일때 곱셈의 역원이 존재하기 때문에 는 소수(의 거듭제곱(이여야 합니다.
이때 곱셈의 역원(inverse)는 페르마의 소정리를 통해 구할 수 있습니다.
참고로 페르마의 소정리(Fermat’s Little Theorem)는 이렇습니다.
- 가 정수이고, 가 소수일 때, (gcd는 최소공약수) 이면 이다.
- 이를 변형한다면 이 될 수 있고,
- 이에 따라 역원은 이다.
따라서
- 등은 유한체가 존재하지만()
- 같은 경우는 유한체가 존재하지 않습니다.
그런 유한체는 보통 다른연산도 가능하지만, 모듈러 연산에 적용시켜 표현하는 경우가 많습니다.
유한체니까 유한하니 직접 그려봅시다.
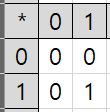
의 곱셈 연산
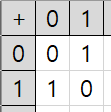
의 덧셈 연산
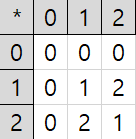
의 곱셈 연산
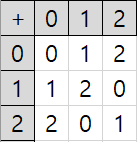
의 덧셈 연산
유한체의 덧셈은 두 원소 내에서의 동일한 승수를 가지는 항에서의 계수의 합을 통해 이루어집니다.
즉 덧셈 및 곱셈에 대해 마지막에 로 모듈러연산(Modular Arithmetic) 을 적용한다고 보면 됩니다.
그렇다면 는 N진수가 아닐까요?
그리고 다시 위의 표를 봅시다.
의 덧셈은 XOR(배타적 논리합)과 같고
의 곱셈은 AND(논리곱)연산과 같습니다.
나눗셈은 1의 역원(inverse)는 1밖에 없기때문에 변화하지 않습니다.
뺄셈 역시 1의 역원(inverse)는 -1이기 때문에 덧셈과 동일합니다.
XOR의 경우 패리티체크, 암호키, 예전 메모리가 부족하거나 임베디드의 경우 메모리를 적게쓰는 swap에 사용됩니다. 꽤나 컴퓨터에서 중요한 연산이죠
그리고 이거.. 어디서 많이본거 아닌가요? 0과 1만을 갖는 정보.
그렇습니다. 현대컴퓨터는 기계어라고 불리는 일정길이의 비트 문자열로 표현합니다.
1바이트, 8비트의 정보는 로 표현할 수 있지 않을까요?
또한 이런경우()를 의 확대체(extension Field)라고 합니다.
는 덧셈은 XOR, 곱셈은 비트단위 Shift 와 비트단위 XOR 연산을 사용하기 때문에 컴퓨터에서 속도가 빠릅니다. 따라서 현대 컴퓨터의 기반이 된다고 전 생각합니다.
아, 또한 의 경우 AES(Advanced Encryption Standard)에 사용됩니다.
체로부터 게임은 어떻게 만들어지는가
아주 기초적인 이동부터 생각을 해봅시다.
게임에서 필요한 기본적인 ‘공간’을 구현해야합니다.
2차원이든, 3차원이든 공간을 구성하였다면 객체를 만들것이고,
객체는 위치좌표인 수를 가지고 있습니다.
수는 크기와 방향을 가지고 있습니다. 수직선상에선 부호에 따라 - 와 + 의 방향을 가진다고 볼 수 있습니다.
객체를 평행이동하기 위해서 덧셈연산을 사용합니다.
객체의 크기를 조절하기 위해 객체를 기준으로 한 ‘구성요소의 위치정보들’에 전부 곱셈연산을 사용합니다.
객체의 방향을 돌리기 위해서..는 아직 2차원 좌표계상에서 부호의 곱셈만 처리한다고 놔두겠습니다.
이렇게 좌표처리는 끝납니다.
조건문(명제)를 통해 분기를 결정하고, 분기에 따라 처리를 다르게 진행합니다.
게임의 핵심은 해당 부분이라고 생각합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//주 오브젝트의 좌표정보집합
var mainObjectCollection = new List<int>(){-1,0,1};
//이동에 대한 분기처리
//만약 좌측 화살표를 누른다면
if(Input.GetKeyDown(KeyCode.Left))
{
foreach(var element in mainObjectCollection)
{
element += -1;
}
}
//만약 우측 화살표를 누른다면
if(Input.GetKeyDown(KeyCode.Right))
{
foreach(var element in mainObjectCollection)
{
element += 1;
}
}
이렇게 사용자입력에 따라 명제의 참과 거짓을 판별하여 제어문을 다르게 접근하여 처리한다.
이것이 게임을 이루는 요소중 주 특징인 상호작용(interactive)이라고 생각합니다.
여기까지가 제가 이해하고 작성한 내용입니다.
잘못된 부분이나 수정해야할 사항 코멘트 부탁드립니다.
감사합니다.
