고등학교때 작성한 자료를 최근 질문받은적 있어서 다시 정리해봅니다.
그래서 노가다한 이미지는 없습니다.
1. 머리
GJK 알고리즘(Gilbert-Johnson-Keerthi Algorithm)은 두 개의 볼록한 형태(Convex Shapes), 주로 메쉬 혹은 시간이 변화한 콜라이더 사이의 충돌 여부를 효율적으로 판별하기 위해 사용되는 알고리즘입니다.
이 알고리즘은 주로 물리 엔진이나 게임 엔진, 특히 유니티와 같은 게임 엔진에서 충돌 감지 시스템에 사용됩니다.[1] 이 알고리즘은 객체가 고속으로 이동할 때, 벽을 뚫고 지나가는(터널링) 등의 충돌 감지 문제를 해결하는 데 도움을 줍니다.
[1] (아마 요즘 유니티는 Speculative CCD, Sweep-based CCD (Continuous Collision Detection)를 사용하는 것으로 기억합니다)
2. 기본 개념
GJK 알고리즘은 두 개의 볼록한 다면체(Convex Polyhedron) 사이의 최소 거리 혹은 교차 여부를 계산하기 위해 사용됩니다. 기본적으로 이 알고리즘은 Minkowski Difference를 이용하여 두 형태가 교차하는지(원점을 Convex hull 내부에 포함하는지) 확인합니다.
Minkowski Difference (민코우프스키 차): 두 집합 A와 B가 있을 때, Minkowski Difference는 A와 -B의 모든 벡터 차이의 집합을 의미합니다. 여기서 -B는 B의 모든 점의 방향을 반대로 바꾼 집합입니다. 이는 두 형태 사이의 충돌 여부를 단순화하여 원점이 Minkowski Difference 내부에 있는지를 확인함으로써 해결합니다.
Minkowski Difference의 예:
- 점 A가 (x1, y1)이고 점 B가 (x2, y2)라면, Minkowski Difference는 (x1 - x2, y1 - y2)로 계산됩니다.
- 더 복잡한 형태의 경우, A의 모든 점들과 B의 모든 점들 간의 모든 가능한 차이 벡터를 계산하여 집합을 만듭니다.
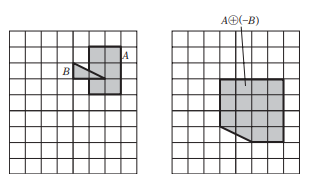민코우프스키 차
3. 알고리즘 단계
GJK 알고리즘은 대충 3가지 개념과 3개의 단계로 이루어집니다.
- 지원 함수 계산: 주어진 방향에서 가장 멀리 있는 점을 찾는 함수입니다. 이 함수를 통해 Minkowski Difference의 표면에서 새로운 점을 찾습니다.
- 볼록껍질(Convex hull) 갱신: 새로운 점을 추가하여 단순체를 갱신하고, 이 단순체가 원점을 포함하는지 확인합니다.
- 반복: 단순체가 원점을 포함할 때까지 혹은 더 이상 볼록껍질(Convex hull)를 확장할 수 없을 때까지 위 과정을 반복합니다.
(여기에 이제 기존에 작성했던 예시를 넣으면 적당한데, 없습니다)
4. 장점과 단점
장점:
- 효율적이고 빠른 계산: GJK 알고리즘은 대부분의 경우 빠른 성능을 보여줍니다.
- 볼록 형태에 대한 정확한 충돌 감지: 두 볼록한 형태 간의 충돌을 정확히 감지할 수 있습니다.
단점:
오목한 형태에 대한 적용 어려움: 오목 형태(concave Hull)에 대해서는 직접적으로 적용하기 어렵습니다.
(예를 들면 회전운동의 경우라거나, 메쉬 자체가 오목한 형태를 띄면 좀 힘듭니다)초기 단순체 설정의 중요성: 초기 단순체가 잘못 설정되면 알고리즘이 실패할 수 있습니다.
참고
- Gilbert, E. G., Johnson, D. W., & Keerthi, S. S. (1988). A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE Journal on Robotics and Automation, 4(2), 193-203.
- Ericson, C. (2004). Real-Time Collision Detection. Morgan Kaufmann.