(🔒)번역 - BRDF Layered Diffuse

Posted May 14, 2024

By Jung Jisang

40 min read

개인공부를 위한 개인페이지입니다.

저작권 관련 문제사항 발생시 삭제될 수 있습니다.

들어가기에 앞서

I3D 2022에 출간된 자료이며, 이해를 돕기 위해 글만 한글로 번역합니다.

유니티의 클리어코트와 유사한 개념으로, 이를 염두해두고 읽으면 읽기 편하지만,

추가적인 통계적접근방식을 통한 다중산란과 차원축소을 포함한 개념의 차이점을 두면 좋습니다.

간단한 리뷰는 다음과 같습니다.

개요

이 논문은 실시간으로 램버트 기저에 거친 유전체 계면이 코팅된 표면(세라믹과 같은 외관)을 렌더링하기 위한 새로운 셰이딩 모델을 제시합니다. 이러한 표면은 흡수 매질로 분리되어 있습니다.

주요 기여

새로운 셰이딩 모델: 두 개의 BRDF 로브로 구성된 모델을 제안하여, 층 구조에서 빛 전송의 처음 세 가지 모멘트를 수치적으로 연구해 구축.
실시간 호환성: 차원 축소를 통해 필요한 테이블을 관리 가능한 크기로 압축하여 실시간 제약에 맞게 조정.
층상 BRDF 프레임워크 확장: Belcour [2018]의 층상 BRDF 프레임워크에 램버트 계면 지원을 추가하여, 실시간으로 물리적으로 기반한 외관의 범위를 확장.

구현 세부 사항

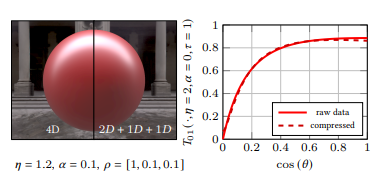
차원 축소: 거친 투과율을 4D에서 2D + 1D + 1D로 압축. 흡수와 거칠기에 대해 각각 2개의 기저를 사용.
GLSL 프래그먼트 셰이더: GLSL 프래그먼트 셰이더로 구현하여 RTX 2070에서 720p 해상도로 프레임당 약 0.5ms 소요.
Unity 통합: Unity의 HDRP에 커스텀 포워드 패스로 포팅, 인터랙티브 프레임 레이트로 실행되며 아티스트가 텍스처로 매개변수를 자유롭게 변경할 수 있음.

검증

Mitsuba 플러그인: Mitsuba 렌더링 엔진의 커스텀 플러그인을 통해 검증, 확률적 참조 모델과 비교하여 정확성을 확인.
다층 재료 검증: Mitsuba 엔진에서 업데이트된 추가-이중화 알고리즘을 사용하여 두 개의 유전체 층과 램버트 기저로 구성된 표면의 외관을 재현.

한계

임계각: $\eta < 1$ 인 경우 임계각에서 뚜렷한 불연속성이 발생하며, GGX 로브로 이를 완전히 재현할 수 없음.
이방성과 참여 매질: 거친 등방성 유전체 코팅으로 제한, 매질 내 다중 산란을 고려하지 않음.

유니티 클리어코트와의 비교

다중 산란 처리: 논문의 모델은 다중 산란을 고려하여 더 정확한 빛의 상호작용을 재현합니다. Unity의 Clear Coat는 이러한 복잡한 상호작용을 단순화한 형태로 제공할 수 있습니다.
차원 축소: 논문에서는 필요한 데이터의 차원을 축소하여 실시간 성능을 향상시키는 방법을 제시합니다.

Rendering Layered Materials with Diffuse Interfaces

Heloise de Dinechin (Unity Technologies, EPFL)
Laurent Belcour (Unity Technologies)

원문 :

https://belcour.github.io/blog/research/publication/2022/04/13/brdf-layered-diffuse.html

https://arxiv.org/pdf/2203.11835

개요(ABSTRACT)

본 연구에서는 실시간으로 거친 유전체 코팅(rough dielectric coating)을 가진 램버트 표면을 렌더링하는 새로운 방법을 소개합니다.

이러한 구성의 외관이 각각 직접 및 간접 상호작용을 설명하는 두 개의 마이크로페싯 로브(microfacet lobes)로 충실하게 표현된다는 것을 보입니다.

우리는 5차원 테이블을 사용하여 빛 전송의 1차 방향 통계(에너지, 평균 및 분산)를 기반으로 이러한 로브를 수치적으로 맞추고, 이를 분석적 형식과 차원 축소를 통해 2차원 + 1차원으로 좁힙니다.

우리는 거친 플라스틱과 세라믹을 효율적으로 렌더링하여 우리 방법의 품질을 입증하며, 이는 진실에 매우 가깝습니다. 또한, 우리는 최첨단의 층상 물질 모델을 개선하여 램버트 계면을 포함시켰습니다.

CCS Concepts

Computing methodologies → Reflectance modeling

Keywords

Layered Materials, Statistical Analysis, Real-Time Rendering

ACM Reference Format:

Heloise de Dinechin and Laurent Belcour. 2022. Rendering Layered Materials with Diffuse Interfaces. In Proceedings of SIGGRAPH I3D (I3D’22). ACM, New York, NY, USA, 7 pages. https://doi.org/10.1145/3522620

1. 소개(INTRODUCTION)

머테리얼 모델을 실시간 렌더링 엔진과 오프라인 렌더링 엔진 모두와 호환되게 설계하는 것은 도전적인 과제입니다. 많은 경우, 실시간 셰이딩 모델은 오프라인 렌더링 모델을 조악하게 근사합니다.

예를 들어, 코팅된 세라믹 또는 거친 코팅 플라스틱의 경우, 램버트 기저 위에 거친 유전체 코팅이 쌓인 구조로 정의됩니다. 이러한 재료를 근사하기 위해, 실시간 모델은 보통 거친 스펙큘러(rough specular) 로브와 확산 로브를 아티스트가 정의한 값으로 혼합하여 빛 전송을 무시합니다.

그러나 오프라인 모델은 코팅과 기저 간의 상호작용을 올바르게 평가하여 전송된 확산 색상의 올바른 채도와 밝기를 달성할 수 있지만, 효율성을 희생해야 합니다.

본 연구에서는 실시간으로 그러한 구조를 렌더링하면서도 진실에 가까운 시각적 결과를 제공하는 모델을 제안합니다. 우리의 모델은 간단한 아이디어에 기반합니다.

먼저, 단일 및 다중 산란 간층의 1차 방향 통계(에너지, 평균 및 분산)를 표로 작성합니다. 그런 다음, 이러한 통계를 근사하는 BRDF 로브의 합을 사용합니다.

램버트 계면이 빛 전송 적분을 비상관화(decorrelation)하는 사실을 이용하여 이러한 통계를 원자적 사전 계산으로 축소하고, 분석적 표현식과 결합합니다.

이러한 통계를 일치시키는 GGX 마이크로페싯 모델 [Walter et al. 2007]의 BRDF 로브를 사용하여, 우리는 확률적 참조와 매우 유사한 근사 모델을 얻습니다.

GPU의 텍스처 유닛을 더 잘 활용하기 위해, 사전 계산된 테이블을 반복적인 차원 축소를 사용하여 2D 텍스처로 압축합니다. 우리는 이 모델을 더 발전시켜 Belcour [2018]의 통계적 프레임워크에 램버트 계면을 통합합니다.

2. 이전 연구 (PREVIOUS WORK)

수직으로 쌓인 개별 계면으로 이루어진 재료는 층상 재료(layered materials)라고 합니다 [Weidlich and Wilkie 2007] (그림 2 (a)). 문헌은 특정 구성에 대한 폐쇄형 모델을 나타내는 방법과 임의의 층 수를 결합하는 프레임워크로 나눌 수 있습니다.

특정 모델은 특정 층 수에 대한 폐쇄형 표현식을 제공합니다. 예를 들어, Four-Flux Matrix 방법 [Simonot et al. 2016]은 유전체 코팅과 램버트 기저 사이의 전송을 특정하게 모델링합니다. 그러나 이 방법은 현재 실시간 렌더링에 필수적인 프리필터링된 조명(HDRI나 면조명)과 호환되는 모델을 제공하지 않습니다.

오프라인 층상 재료 프레임워크. 일반적인 프레임워크를 설계할 때의 어려움은 층 구조 내의 다중 산란을 설명하는 데 있습니다. 스펙트럼 표현 [Jakob et al. 2014; Zeltner and Jakob 2018]은 이러한 모델을 평가하는 데 효율적입니다. 여기서 반사율은 푸리에 기저에서 분해되며, 추가-이중화 알고리즘 [van de Hulst 1980]은 다중 산란을 설명합니다. 그러나 이것은 텍스처 사용을 금지하며 높은 평가 오버헤드를 필요로 합니다. 확률적 방법 [Gamboa et al. 2020; Guo et al. 2018]은 반사율을 평가하기 위해 몬테카를로 방법을 사용합니다. 이들은 정확성을 노이즈과 맞바꾸며, 그로 인해 셰이딩에 분산을 추가하여 오프라인 시나리오로 사용이 제한됩니다.

실시간 층상 재료 프레임워크. Elek [2010]은 Weidlich와 Wilkie [2007]의 모델을 실시간 렌더링에 적용했습니다. 그러나 원래 방법과 마찬가지로, 적절한 다중 산란 평가가 부족하며, 점광원만을 지원합니다. 마지막으로, 통계 모델 [Belcour 2018; Guo et al. 2016]은 구조 내에서 다중 산란의 통계를 재현하는 방향성 알베도, 입사 방향 및 거칠기를 가진 마이크로페싯 로브의 합으로 반사율을 근사합니다. 이를 통해 실시간으로 확장된 광원을 렌더링할 수 있습니다. 많은 확장에도 불구하고 [Randrianandrasana et al. 2021; Weier와 Belcour 2020; Yamaguchi et al. 2019], 이 모델은 램버트 계면을 처리하지 못합니다.

기여 요약. 본 연구에서는 통계 프레임워크를 사용하여 램버트 계면을 처리할 수 있도록 확장함으로써 더 다양한 구성을 렌더링할 수 있게 합니다. 이를 위해, 우리는 램버트 기저 위에 거친 유전체 코팅을 쌓은 구조(거친 코팅 램버트, 그림 2 (b))의 통계를 연구합니다. 이러한 통계로부터 우리는 그러한 재료에 대한 반사율 모델을 구축하고, 램버트 기저와의 구성을 처리할 수 있도록 통계적 층상 프레임워크를 개선합니다(그림 2 (c-d)).

3. 코팅된 램버시안의 통계

거친 코팅 램버트 반사율

거친 코팅 램버트 반사율은 코팅에 의해 직접 반사된 빛과 램버트 기저에 의해 간접적으로 반사된 빛의 합입니다. 우리는 결과적인 BRDF 모델을 두 가지 항으로 분해하기로 했습니다: 직접 항 $\rho_1$ 과 간접 항 $\rho_{2+}$ 입니다. 직접 항은 이전 연구 [Belcour 2018]에서 이미 설명되었습니다. 간접 항의 경우, 우리는 그 에너지, 평균 및 분산을 연구합니다.

3.1 에너지

다중 산란 성분 $\rho_{2+}$ 의 에너지는 램버트 기저와 한 번 상호작용하는 경로의 적분입니다. 이들은 $\eta_1$ 에서 $\eta_2$ 로의 거친 굴절 $T_{01}$ , 확산 상호작용 $\rho (x)$ , 그리고 $\eta_2$ 에서 $\eta_1$ 로의 거친 반사와 굴절 $\bar{R}*{10}$ 및 $\bar{T}*{10}$ 을 겪습니다:

\rho_{2+} = \sum_{\Omega_n} \int_{x \in \Omega_n} T_{01}(x_0)\rho (x_1) \left( \prod_{k=2}^{n-2} \bar{R}{10}(x_k)\rho (x{k+1}) \right) \bar{T}_{10}(x_n)

여기서 $x = x_i [0,n] \in \Omega_n$ 은 길이 $n$ 의 모든 경로입니다. 램버트 상호작용으로 인해, 각 버텍스에서의 적분은 비상관화(decorrelation)됩니다:

\rho_{2+} = \sum_{n} T_{01} \rho \left( \prod_{k=2}^{n-2} \bar{R}{10} \rho \right) \bar{T}{10}

= \sum_{k=0}^{\infty} T_{01} \rho^{k+1} \bar{R}{k10} \bar{T}{10}

여기서 $T_{01} = \int T_{01}(x)dx$ 입니다. 이 형태는 수렴하는 급수입니다:

\rho_{2+} = T_{01} \frac{\rho}{1 - \rho \bar{R}{10} \bar{T}{10}}

여기서 $\bar{T}*{01}$ 은 $\eta$ , $\alpha$ , 입사각에 따라 달라지며, $\bar{R}*{10}$ 과 $\bar{T}_{10}$ 은 $\eta$ 와 $\alpha$ 에 따라 달라집니다 (그림 3 (a-c) 참조). 따라서, 이는 4차원 함수 대신 3차원 및 2차원 함수로 에너지를 표현합니다.

3.2 평균

간접 로브의 평균은 항상 셰이딩 법선입니다. 실제로, 램버트 상호작용은 셰이딩 법선을 중심으로 반구에서 에너지를 대칭적으로 분배합니다. 이후의 거친 투과와 거친 반사는 이러한 대칭을 변경하지 않습니다.

3.3 분산

우리는 가상 고니오포토미터(고니오 광도계,광원을 측정할 때 사용되는 기구)를 사용하여 투영된 접선 평면에서 방향 분산을 기록했습니다. 입사 방향에 의해 빛 분포가 영향을 받지 않기 때문에, 우리는 확산 기저에서 광선을 시작하여 코팅된 램버트 구조에서 경로를 추적했습니다. 따라서, 우리는 2차원 테이블 $\sigma^2_{+}(\eta, \alpha)$ 을 얻었으며, 이를 그림 3 (d)에 표시했습니다.

3.4 근사 모델

이 데이터를 사용하여 거친 코팅 램버트 모델을 두 개의 BRDF 로브의 합으로 인스턴스화할 수 있습니다: 거칠기 $\alpha$ 와 굴절률(IOR) $\eta$ 의 GGX 노멀 분포에 의한 반사만을 고려한 고전적인 마이크로페싯 모델 BRDF1과 간접 항 BRDF2+:

BRDF (\omega_i, \omega_o) = BRDF1 (\omega_i, \omega_o) + BRDF2+ (\omega_i, \omega_o),

두 번째 항은 다음과 같습니다:

BRDF2+ (\omega_i, \omega_o) = \rho_{2+} \frac{D(n, \omega_o, \alpha_{2+}) \bar{G}(n, \omega_o, \alpha_{2+})}{4 \cos(\theta_i) \cos(\theta_o)},

여기서 $D(\cdot, \cdot)$ 는 마이크로페싯 분포, $\bar{G}(\cdot, \cdot)$ 는 정규화된 섀도잉/마스킹 항이며, 에너지 손실은 $\rho_{2+}$ 에 포함되어 있습니다. $\alpha_{2+}$ 는 3.3절에서 계산된 분산에 대한 등가 거칠기입니다. 노멀 분포와 섀도잉/마스킹 항은 입사 방향으로 셰이딩 노멀로 평가됩니다.

그림 4에서 이 실시간 모델을 오프라인 참조 모델과 비교합니다. 우리의 작업은 굴절률 $\eta < 1$ 과 같이 어려운 구성을 일치시키며, 여기서 전체 내부 반사는 유전체 계면의 거칠기에 따라 매끄러움이 달라지는 이동 불연속을 생성합니다. 이러한 구성은 더 많은 층을 추가하거나 수중 장면을 렌더링하려면 고려해야 합니다.

4. 차원 축소

우리의 모델은 Beer-Lambert 소멸 법칙을 처리하기 위해 $\tau = \exp (-\sigma _ \alpha)$ 를 $T_{01}$ , $\bar{T}*{10}$ , $\bar{R}*{10}$ 의 추가 차원으로 추가합니다. 그러나 $T_{01}$ 에 대한 밀집된 4D 테이블을 GPU에 저장하는 것은 금지됩니다. 우리는 주성분 분석(PCA)을 적용하고 이를 1D 기저 테이블과 3D 계수 테이블로 분해하여 데이터의 차원을 줄입니다:

T_{01} (\cos(\theta_i), \alpha, \eta, \tau) \approx \sum_{k=0}^{N} c_k (\cos(\theta_i), \alpha, \eta) b_k (\tau).

계수 $c_k (\cos(\theta_i), \alpha, \eta)$ 는 유사한 분해로 추가 분해될 수 있습니다:

c_k (\cos(\theta_i), \alpha, \eta) \approx \sum_{j=0}^{M} c'_j (\cos(\theta_i), \alpha) b'_j (\eta),

따라서:

T_{01} (\cos(\theta_i), \alpha, \eta, \tau) \approx \sum_{k=0}^{N} \sum_{j=0}^{M} c'_j (\cos(\theta_i), \alpha) b'_j (\eta) b_k (\tau).

이 전략을 여러 번 적용하면 테이블의 차원을 줄일 수 있습니다. 마지막 차원의 변동이 저주파수일 때, 필요한 기저 성분의 수는 적으며 단일 텍스처에 저장할 수 있습니다(예: 4개의 기저 사용). 그림 5에서 이러한 압축의 결과를 보여줍니다.

Untitled

5. 통계적 층상 프레임워크

3장에서 수집한 통계를 바탕으로, 우리는 통계적 층상 프레임워크 [Belcour 2018]에 램버트 계면 지원을 추가합니다. 이를 위해, 우리는 마지막 유전체 계면과 램버트 계면을 하나의 층 인터페이스로 그룹화합니다. 다른 층과 달리, 이 새로운 층은 두 개의 BRDF 로브를 출력합니다. 이 추가적인 로브를 전파하기 위해, 우리는 추가-이중화 알고리즘에 또 다른 집합의 방향 통계를 추가하고 (그림 6), 이를 업데이트합니다 (알고리즘 1).

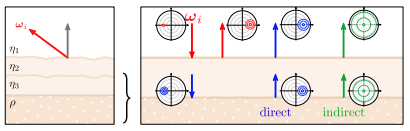
Untitled

이러한 통계적 접근 방식을 통해 다양한 층 간의 상호작용을 더 정확하게 모델링할 수 있으며, 특히 램버트 계면과 같은 복잡한 구조를 포함한 재료를 보다 현실감 있게 렌더링할 수 있습니다.

추가-이중화 알고리즘

통계적 프레임워크 내에서, 연산자는 빛이 층에 의해 반사되거나 굴절될 때 방향 모멘트(에너지 𝑒, 평균 𝜇, 분산 𝜎)의 변화를 설명하는 데 사용됩니다.

이러한 국부 통계는 표면 위에서 들어오는 빛에 대한 전송 및 반사 계수: $(t_{0i})$ 와 $(r_{0i})$ , 그리고 표면 아래에서 들어오는 빛에 대한 전송 및 반사 계수: $(t_{i0})$ 와 $(r_{i0})$ 와 같은 전역 통계를 업데이트하는 데 사용됩니다.

모든 계수는 추가-이중화 알고리즘 동안 계산되며, 재료의 반사율을 근사하는 다양한 로브를 평가하는 데 결합됩니다.

새로운 연산자

우리는 거친 코팅 램버트를 위한 연산자를 두 개의 연산자로 분해합니다: 하나는 거친 유전체 반사를 위한 연산자이고, 다른 하나는 다중 산란 성분을 위한 연산자입니다. 후자는 수학적으로 다음과 같이 정의됩니다:

e = \rho_{2+} \text{ (Equation 3에서 정의됨)} \\ \mu = 0 \text{ (셰이딩 노멀과 정렬됨)} \\ \sigma = \sigma_{2+} \text{ (표에 기록됨, 그림 3 (d) 참조)}

이로 인해 셰이딩 노멀을 중심으로 하는 추가적인 로브가 생성됩니다 (그림 6, 녹색 로브). 평균과 분산이 다르기 때문에, 이 로브에는 전송 계수 (t_{i0})가 유효하지 않으며, 추가 공식을 적용할 수 없습니다. 따라서, 우리는 추가-이중화 알고리즘에 램버트 로브에 대한 특정 경우를 추가합니다.

추가-이중화 알고리즘의 수정

이 추가 로브를 고려하기 위해, 우리는 추가-이중화 알고리즘의 일부만 수정합니다. 유전체 계면의 처리는 여전히 Belcour [2018]의 구현을 따릅니다 (알고리즘 1에서 색으로 강조된 차이점을 참조).

알고리즘이 마지막 유전체 계면에 도달하면, 추가-이중화 공식을 사용하여 직접 반사된 로브를 추가하지만, 간접 로브는 다르게 처리합니다: 이 로브는 셰이딩 노멀과 정렬된 평균을 가지므로, 추가-이중화 패스 동안 계산된 전송 및 반사 계수를 사용할 수 없습니다.

이러한 계수는 간접 로브의 평균과 분산을 사용하여 모든 계면에 대해 재평가되어야 합니다.

  
# 의사코드

def updated_adding_doubling_algorithm(layers):
    # 초기화
    r0i, ri0 = 0, 0  # i 층의 반사율
    t0i, ti0 = 1, 1  # i 층의 투과율
    sigma_R0i, sigma_Ri0 = 0, 0  # i 층의 반사율 분산
    sigma_T0i, sigma_Ti0 = 0, 0  # i 층의 투과율 분산
    ji0 = 1  # i 층에서 최상층으로의 Jacobian

    # 유전체 로브를 평가하기 위한 상단에서 하단으로의 루프
    for i in range(len(layers)):
        # 에너지 업데이트
        r0i, ri0, t0i, ti0 = update_energy()
        sigma_R0i, sigma_Ri0, sigma_T0i, sigma_Ti0 = update_variance()

        # 새로운 로브를 BRDF 로브 목록에 추가
        m = ri0 * r0i / (1 - ri0 * r0i)
        add_lobe(t0i * r0i * ti0 / (1 - ri0 * r0i), wr, sigma_Ti0 + ji0 * (sigma_T0i + sigma_Ri * m * (sigma_Ri + sigma_Ri0)))

        # Jacobian 업데이트
        ji0 = ji0 * ji

    #(수정사항) 거친 코팅 램버트의 유전체 코팅 추가
    add_lobe(t0i * rN * ti0 / (1 - ri0 * rN), wr, sigma_Ti0 + ji0 * (sigma_T0i + sigma_RN * m * (sigma_RN + sigma_Ri0)))

    #(수정사항) 램버트 로브를 평가하기 위한 하단에서 상단으로의 루프
    riN = t0i * eval_reflectance()  # Equation (9)
    sigma_iN = eval_variance()  # Equation (11)
    for i in reversed(range(len(layers) - 1)):
        riN = (riN * ti) / (1 - ri * ri + 1)
        sigma_iN = ji * sigma_iN + sigma_Ti + ji * (sigma_Ri + sigma_Ri + 1) * ri * ri + 1 / (1 - ri * ri + 1)
        sigma_iN = max(sigma_iN, sigma2_plus(eta_i, alpha_i))
    
    add_lobe(riN, n, sigma_iN)

우리는 하단에서 상단으로의 루프를 사용하여 이를 수행합니다.

이는 실제로 램버트 층에 의해 조명된 층 구조에서 투과율에 대해 추가-이중화를 수행하는 것과 동일합니다 (알고리즘 의 수정 사항). 즉, 우리는 하단에서 상단으로 반사 계수와 분산을 업데이트합니다:

r_{iN} = \frac{r_{i-1N} t_i}{1 - r_i r_{i+1}}\\ \sigma_{Ni} = j_i \sigma_{Ni-1} + \sigma_{Ti} + j_i \left( \sigma_{Ri} + \sigma_{Ri+1} \right) \frac{r_i r_{i+1}}{1 - r_i r_{i+1}}

원 논문의 방정식을 사용하여.

높은 분산

유전체 계면을 통해 전송할 때 계산된 분산은 유전체 층을 통한 확산 전송의 분산을 초과해서는 안 됩니다. 따라서 우리는 이를 사용하여 분산을 클램핑합니다:

\sigma_t = \min(\sigma_t, \sigma_2^+(\eta, \alpha))

6. 구현 세부 사항

차원 축소

우리의 구현에서, 우리는 거친 투과율 $T_{01}$ 을 4D에서 2D + 1D + 1D로 압축하고, 확산 투과율 $\bar{T}*{10}$ 및 확산 반사율 $\bar{R}*{10}$ 을 3D에서 2D + 1D로 압축합니다. 흡수 $\tau$ 에 대해서는 2개의 기저를 사용하고, 거칠기 $\alpha$ 에 대해서는 2개 또는 4개의 기저를 사용합니다.

후자의 경우, 2개의 기저는 1개의 RGBA 텍스처만 필요하지만, 4개의 기저는 2개의 텍스처가 필요합니다. 우리는 보충 자료에서 재구성의 품질을 보여줍니다.

거친 코팅 램버트의 2차 로브

우리의 분석에 따르면, $\eta > 1$ 의 경우 거친 코팅 램버트의 2차 로브는 시각적으로 확산 로브와 가깝습니다. 근사 GGX 로브(입사 방향으로 셰이딩 노멀을 사용) 또는 확산 로브를 사용하면 유사한 외관을 얻을 수 있습니다.

그러나 $\eta < 1$ 의 경우에는 그렇지 않습니다. 이 경우 로브의 분산은 전반사(TIR)에 의해 제한되며, 등가 분산을 가진 GGX 로브가 불연속성을 일치시킵니다(그림 11 참조).

7. 결과

Mitsuba에서의 검증

우리는 Mitsuba [Jakob 2010]의 커스텀 플러그인을 통해 거친 코팅 램버트 모델을 검증했습니다. 이 커스텀 플러그인을 임의의 층상 재료를 렌더링할 수 있는 확률적 참조 모델과 비교했습니다 (Guo [2018]와 유사).

그림 7은 일부 유닛 테스트를 보여줍니다. 추가 결과와 소스 코드는 보충 자료를 참조하십시오. Weidlich와 Wilkie [2007]의 이전 실시간 호환 모델과 달리, 우리의 모델은 다중 산란을 고려합니다(그림 8 참조).

우리는 $\eta < 1$ 의 구성이 그럴듯한 분포를 생성함을 확인했습니다 (그림 7, 왼쪽 열). 여기서 내부의 빨간 원판은 램버트 기저로 전송된 광선을 나타내고, 원판의 외부는 순수 반사를 나타냅니다.

이러한 구성은 현실적이지 않지만, 서로 다른 재료를 층층이 쌓을 때 중요합니다.

실시간 프로토타입

우리는 거친 코팅 램버트 모델을 GLSL 프래그먼트 셰이더로 구현했습니다.

이 데모는 환경 맵을 위해 사전 필터링된 이미지 기반 조명 [Lagarde and De Rousiers 2014]을 사용합니다. 이 셰이더는 Mitsuba의 확률적 참조와 시각적으로 일치합니다(그림 4 참조).

이 프로토타입에서, RTX 2070에서 720p 해상도로 전체 화면을 셰이딩하는 데 프레임당 약 0.5ms가 소요되었습니다. 자세한 내용은 비디오를 참조하십시오.

Unity에서의 렌더링

우리는 이 셰이더를 Unity의 고해상도 렌더 파이프라인 [Lagarde et al. 2018]에 커스텀 포워드 패스로 포팅했습니다. 여기서 우리의 모델은 인터랙티브 프레임 레이트로 실행되며, 아티스트가 텍스처로 매개변수를 자유롭게 변경할 수 있습니다.

그림 1에서 우리는 코팅된 세라믹과 래커 표면의 외관을 재현했습니다. 이는 알베도와 거칠기(왼쪽) 또는 굴절률(오른쪽)을 텍스처링하여 수행했습니다.

그림 9에서는 흡수 $\tau$ 를 사용하여 알베도만으로는 재현할 수 없는 고니오크로매틱(goniochromatic, 관찰 각도에 따라 색상이 변하는 특성) 효과를 추가하는 방법을 보여줍니다.

층상 재료의 검증

우리는 업데이트된 추가-이중화 알고리즘을 Mitsuba 렌더링 엔진에 구현했습니다. 여기서 우리는 램버트 기저 위에 2개의 유전체 층으로 구성된 표면의 외관을 재현했습니다. 우리의 모델을 확률적 참조와 비교했으며, 우리의 모델이 시각적으로 참조에 가깝다는 것을 보여줍니다(그림 10).

8. 한계

임계각

거칠기가 매우 작고 $\eta < 1$ 인 경우, 임계각은 결과 BRDF에서 뚜렷한 불연속성을 생성합니다. 우리가 이러한 분포를 GGX 로브로 근사하고 있기 때문에 이를 재현할 수 없습니다.

이 효과는 반사율 $R_{01}$ 과 투과율 $T_{01}$ 에 의해 완화되지만, 이 경우 재구성의 품질은 해당 테이블의 해상도에 따라 달라집니다.

이방성과 참여 매질

우리는 모델을 거친 등방성 유전체 코팅으로 제한했습니다. 그러나 사전 계산된 테이블에 추가적인 거칠기 차원을 추가하는 것은 방법의 핵심을 변경하지 않을 것입니다.

우리는 몇 개의 기저 성분을 사용하여 이 차원을 줄일 수 있을 것이라고 가정합니다. 또 다른 제한 사항은 매질 내에서 다중 산란을 고려하지 않았다는 것입니다.

이러한 전송은 많은 로브 방향을 추적해야 하며 [Randrianandrasana et al. 2021], 이는 성능에 부정적인 영향을 미칩니다.

9. 결론

우리는 램버트 기저 위에 거친 유전체 계면이 코팅되고 흡수 매질로 분리된 세라믹과 유사한 표면을 실시간으로 렌더링하기 위한 새로운 셰이딩 모델을 제시했습니다. 우리는 층 구조에서 빛 전송의 처음 세 가지 모멘트에 대한 수치적 연구를 바탕으로 이 모델을 구축했습니다.

두 개의 BRDF 로브로 구성된 우리의 모델이 실제 값을 정확하게 재현함을 보였습니다. 우리는 필요한 테이블을 차원 축소를 통해 관리 가능한 크기로 압축하여 이 모델을 실시간 제약에 맞게 조정했습니다. 이러한 통계를 활용하여 Belcour [2018]의 층상 BRDF 프레임워크에 램버트 계면 지원을 추가했습니다. 이를 통해 실시간으로 물리적으로 기반한 외관의 범위를 넓힐 수 있게 되었습니다.

비밀번호:

Graphic, Translate

This post is licensed under CC BY 4.0 by the author.

Contents