여는장

특정 점의 색상을 적은 데이터를 통해 얻을려면 어떻게 해야할까요?

1차원

보통 1차원 수직선에서 사용하는 Gradient를 생각해보면 편합니다.

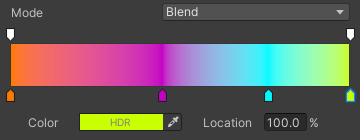
Untitled

gradient는 몇몇 포인트에서의 색상을 지정한 뒤,

어떤 지점의 색상 구하고자 한다면 을 연관된 포인트의 색상들을 조합해서 만들게 됩니다.

이 과정을 Evaluation (평가, 저는 ‘측정’이라는 번역을 선호합니다)라고 합니다.

2차원

2차원으로 간다면 어떻게될까요?

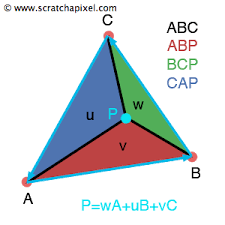
Untitled

삼각형의 무게중심을 통해 색상영역을 구하게 됩니다.

그리고 여기서 샘플링을 추가하게 된다면 텍스처도 입힐 수 있게 됩니다.

3차원

그러면 3차원에서는 어떻게 사용하면 될까요?

cubic? 물론 맞는말입니다. 큐브맵 샘플링이 그 방식이죠.

tetrahedral? 이 또한 맞는말입니다. 무게중심좌표계를 단순히 늘리면 가능하죠.

인접한 프로브의 색상을 혼합할 때 사용합니다.

모든 공통점은 “‘특정 방향’에 지정된 색상과의 조합” 이라고 볼 수 있습니다.

특정방향은 기저(basis)일수도, 삼각형의 각 버텍스일 수도 있습니다.

이러한 방식들 고차원적인 방법으로 확장할 수 있습니다.

이제 다룰 구면조화(Spherical Harmonics, SH)입니다.

조화 함수란?

조화- 라는 접두사 혹은 접미사가 붙는 많은 단어들이 있습니다.

물리에서의 조화진동자, 수학에서 배우는 조화평균, 전기공학의 조화전류, 구면조화와 조화맵핑. 모두 여기에 해당됩니다.

이 조화-가 붙는다는 뜻은 주로 시간에 따른 변화가 정현파(주기적이고 반복적인)를 나타내는 것을 의미합니다. 이런 정현파는 간단하고 예측가능한 형태를 띄며, 푸리에 분석에도 적합하며 *중첩원리가 적용되기 쉽습니다.

중첩원리 : 선형 미분방정식의 해의 선형결합(Linear combination of linear differential equation’s solution)이 선형 미분 방정식의 또다른 해(Another solution of linear differential equation)가 된다는 원리

구면조화(Spherical Harmonics)

구면조화는 간단하게 설명하면 둥근 구의 표면 위를 단순한 구성요소로 나누는 방법입니다.

위의 조화 함수에서 말한 조화와는 조금 다르지만,

공간적인 패턴과 구조에 초점을 맞춰 시간에 따른 변화가 아닌 공간적 변화를 다룹니다.

이렇게 시간에 따른 변화를 공간적인 분포로 재해석하여 공간적 관점에서 바라본다면 구면 조화와 푸리에 변환같은 개념사이의 유사성을 발견할 수 있습니다. *

유클리드 공간의 3차원에서는 기저벡터가 3개지만,

구면에서는 각 함수를 직교하게 둠으로써 무수히 많은 기저를 갖을 수 있게합니다.

이를 정규 직교성(Orthonormality)이라 말하며, 이 기저들과 현재 표면의 방향을 내적해, 표면에 대한 기저 계수의 합(여기서는 색상)을 구할 수 있습니다.

또한 조화- 즉 규칙성이 있는 함수라는 부분에서 푸리에 변환의 분해 관점과 마찬가지로,

복잡한 함수를 더 간단한 구성요소로 분해 결합 재구성이 가능합니다.

구체적인 적용과 분석방법은 특성에 따라 달라질 수 있습니다.

구면조화는 왜 사용하나요?

구면조화의 특성

직교성(Orthogonality): 구면 조화 함수들은 서로 직교하여, 독립적인 정보를 나타내고 효과적으로 데이터를 분해하고 재구성합니다.
완비 · 완전성(Completeness): 이 함수들은 구면 상의 모든 연속 함수를 정확하게 표현할 수 있는 완전한 기저를 형성합니다.
다양한 주파수 대역: 구면 조화 함수는 다양한 주파수의 특성을 가지며, 데이터를 다양한 세밀도로 분석하고 표현합니다.
*회전에 대한 강인함: 이 함수들은 회전 변환에 대해 안정적이어서 방향에 의존하는 데이터 처리에 유용합니다.
계산 효율성: 3차원 공간에서의 복잡한 문제를 효율적으로 계산할 수 있어, 특히 라이팅 및 반사 계산에 유용합니다.
스케일링과 변환 용이성: 구면 조화 함수는 크기 조정 및 변환을 쉽게 할 수 있어 다양한 크기와 형태의 데이터에 적용 가능합니다.

*추후 설명하겠습니다.

수학과 엔진적 측면

오브젝트의 특정 지점이 받는 빛 성분의 총량을 단순하게 계산하자면,

구체에서의 각 점을 기저에서의 빛의 량의 (구면)선형보간 한 값이라고 추측할 수 있습니다.

주파수 분해를 통한 최적화: 구면 조화 함수의 특성을 통해 복잡한 조명 환경을 다양한 주파수 성분으로 분해할 수 있습니다. 이는 LOD와 관련이 있으며, 장면의 세부 수준에 따라 필요한 주파수 성분만을 사용하여 계산을 수행할 수 있습니다. 예를 들어, 멀리 있는 물체에 대해서는 더 낮은 주파수 성분만을 사용하여 조명을 계산함으로써 성능을 최적화할 수 있습니다. 다만, 현재 유니티는 L2 구형조도파 - SH9 - 만을 사용하고 있습니다.
효율적인 메모리, 대역폭 관리: L2 구형 고조파를 기준으로 하는 SH를 사용하면, 각 색상 채널당 9개, 총 27개의 부동 소수점 데이터만으로 전체 조명 환경을 표현할 수 있습니다. 즉 Vector4 기준 단 8개 만의 변수를 사용하여 처리할 수 있으며, 이는 기존의 큐브맵 텍스처를 저장하는 큐브맵 방식 계산에 비해 VRAM 할당량을 크게 줄일 수 있습니다.
라이팅 계산의 간소화: 라이팅 계산이 주파수 영역에서 수행될 수 있어, 계산 과정이 간소화됩니다. 또한 보통 라이트프로브는 빌드 전에 굽기(bake)때문에 실시간 렌더링에서는 3차원 무게중심좌표만을 계산하면 되기때문에 중요한 성능점 이점을 제공합니다.

게임엔진에서의 구면조화

유니티에서는 라이트프로브를 통한 GI를 받아오는 방식에서 구면조화를 사용합니다.

프로브가 각 지점의 GI를 미리 연산해서 계수를 저장하고,

메쉬렌더러의 주변 4개의 프로브와 무게중심 좌표계를 통한 혼합된 계수를 쉐이더에 전달해

최종적으로 쉐이더에서 해당 표면(노말)방향의 빛을 계산합니다.

이 과정에서 쉐이더 연산에 사용되는 구면조화의

대역Band와 차수에 대해 이해하는것이 중요합니다.

대역(차수)

대역(Band) 혹은 차수 L에서

각 대역은 해당차수의 다항식과 동일(0대역 = 0차 = 상수)하며,

주어진 대역에는 2L+1개의 함수가 존재합니다.

더 정확히 표현하면,

L^{m}_{l}\\ L^{-1}_{1},L^{0}_{1},L^{1}_{1}\\ L^{-2}_{2},L^{-1}_{2},L^{0}_{2},L^{1}_{2},L^{2}_{2}\\

l (각 운동량 양자수 - Angular Momentum Quantum Number):
- 이 값은 함수의 ‘차수’를 나타내며, 구면 위에서 함수가 가지는 ‘구역’의 수를 결정합니다.
- l이 커질수록, 함수는 더 많은 고저차를 가지며, 이는 구면 상에서 더 많은 굴곡을 의미합니다.
m (자기 양자수 - Magnetic Quantum Number):
- m은 −l에서 l까지의 정수로, l에 의해 제한됩니다.
- m은 구면 위의 함수의 ‘방위각 의존성’을 나타냅니다.
- m의 절댓값이 클수록, 함수는 방위각에 대해 더 빠르게 변화합니다.

유니티 엔진에서의 빛 정보는 주로 3차 다항식. 즉 L2 구형 고조파를 이용합니다.

3차 다항식으로 표현하게 된다면 각 색상채널에 대해 2L+1개의 값인 9(1+3+5)개의 값이 필요하므로 7개의 벡터 배열에 담을 수 있게됩니다.

더욱 디테일하게 하자고 L3 구형 고조파를 사용하게 된다면, 각 채널당 16(1+3+5+7)개. 총합 48개의 float값을 가지게 되며,12개의 vector4가 필요하게 됩니다.

시각화 및 기저

아무튼 L2를 아래축으로 대역, 좌우 m에 대해 표현하는 영역을 시각화한 이미지는 다음과 같습니다.

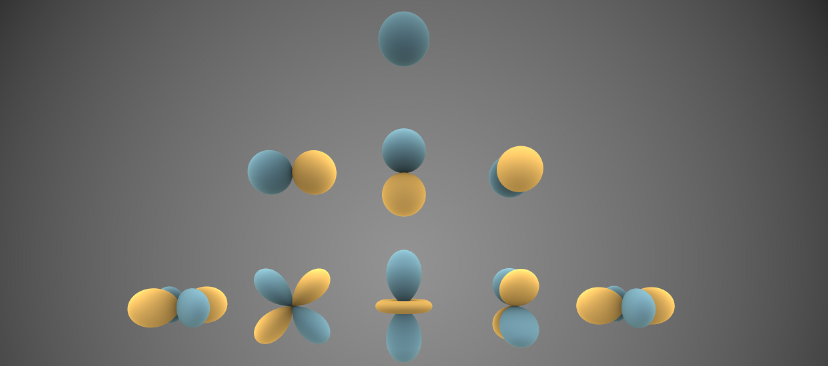
Untitled

해당 방향이 기저라고 생각하면 됩니다.

이를 큐브맵 시각화(붉은색 - 양수, 녹색 - 0, 파란색 - 음수)하면 다음과 같습니다.

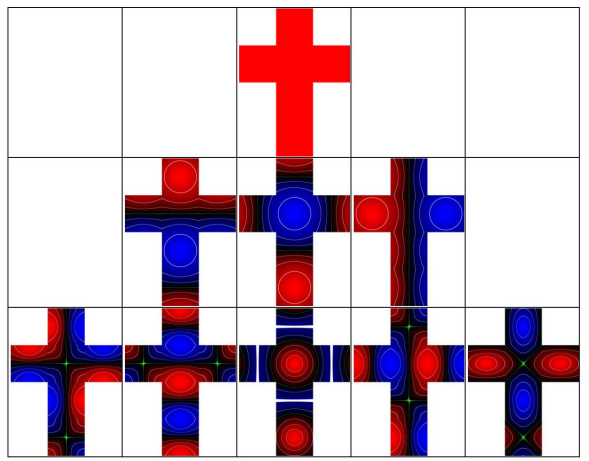
Untitled

해당 기저가 가지는 함수를 표현한다면 다음과 같습니다.

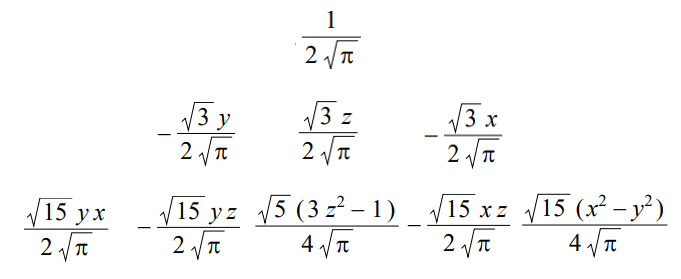
Untitled

여기서 일반적으로 다음과 같은 꼴의 식과, 특정 미지수의 곱으로 분리해서 표현할 수 있는데,

\frac{\sqrt{3}}{2 \sqrt{\pi}},\frac{\sqrt{3 \cdot 5}}{2 \sqrt{\pi}},\frac{\sqrt{3 \cdot3 \cdot 5}}{2 \sqrt{\pi}}

해당식은 정규화 계수(와 조금 섞여있는 르장드르 다항식 상수의 일부) 입니다.

구면함수 - 계수(Coefficients)

정확히는 구면조화함수 Y에 대해 뜯어서 본다면 다음과 같은 형태를 띄게됩니다.

Y^m_n(\theta, \phi) = N_{n}^{m} P_n^m(\cos\theta) e^{im\phi}

\ N_{l}^{m} = \sqrt{\frac{2l+1}{4\pi} \frac{(l-m)!}{(l+m)!}}\\

이 정규화 계수는 수학적 일관성, 즉 일정한 규모나 크기를 가지도록 하는데 큰 역할을 합니다.

또한 정규성을 보장하므로써, 기저가 정규화 되지않았을때의 문제점이 발생하지 않도록 합니다.

어짜피 저 르장드르 다항식과 정규화 계수 - 이하 Coefficients - 들은

실제 쉐이더 연산에서 하기엔 너무나도 잦은, 리얼타임기준 상수값들이므로

라이트프로브를 구울때 미리 계산되어 적용된다고 봐야합니다.

그렇다면 L2에서의 미지수, 저희가 사용할 기저함수는 정리하면 어떻게 될까요?

구면함수 - 기저함수

https://en.wikipedia.org/wiki/Table_of_spherical_harmonics

사실 이에대해서는 이미 친절하게 모두 계산된 식이 존재합니다.

복소평면의 L2의 구면조화의 부호 관례 - Condon-Shortley - 를 본다면 아래와 같지만,

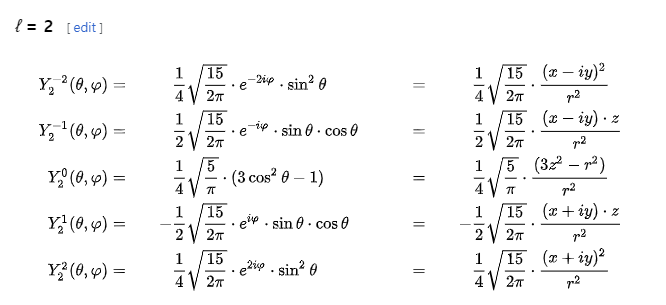
Untitled

엔진에서는 실수부에서만 다루면 되기 때문에 더 간단하게 가져올 수 있습니다.

구면함수 - 기저함수 - L2

바로

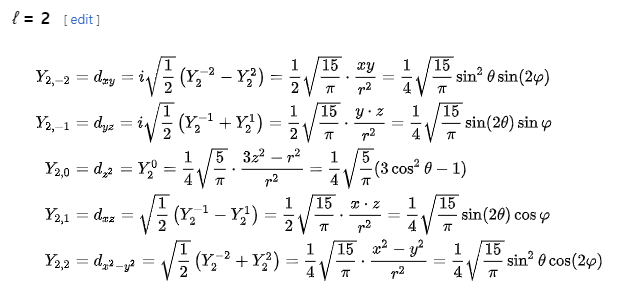
Untitled

와 같이 말이죠.

따라서 중요한 미지수의 곱만 따온다면,

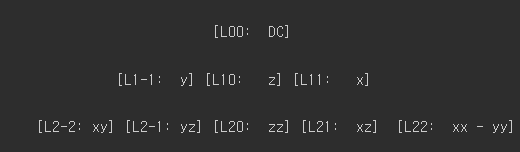
Untitled

으로 표기할 수 있습니다.

이 식은 나중에 쉐이더에서 연산시 스위즐링된 곱으로 만나게 됩니다.

vB = xyzz * yzzx가 뭔소린가 할 때 한번 다시 읽게 됩니다.

구면함수 - 기저함수 - L3

l2까지 밖에 구현이 되어있지 않지만, 만약 l3의 실수 기저함수의 미지수부를 가져온다면

와 같습니다.

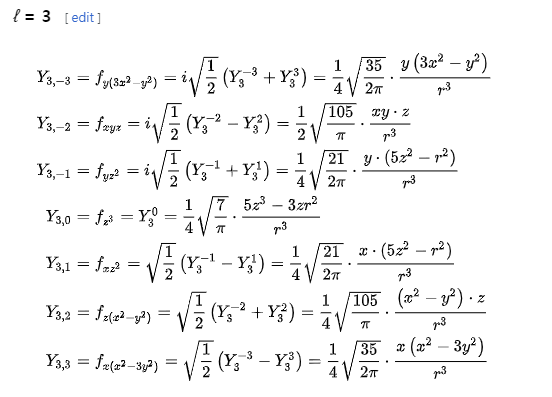
Untitled

이렇게 구현한다면 SampleSH16 을 구현하게 될 것입니다.

사용해보기

위에서 얻은 기반지식을 바탕으로, 데이터를 꺼내써보며

어떻게 구현되어있는지 확인해 볼 차례입니다.

엔진속 SH 꺼내쓰기

LightProbes 클래스의 스태틱함수인 GetInterpolatedProbe를 사용하면

SH정보를 가져올 수 있습니다.

이를 shader에 미리 정의된 Vector4 친구들에 넣어줘,

쉐이더에서 연산할 수 있도록 해봅니다.

  
public void SetSH()
{
    LightProbes.GetInterpolatedProbe(target.transform.position, target, out sh);
    
    for (var i = 0; i < 3; i++)
        SHA[i] = new Vector4(sh[i, 3], sh[i, 1], sh[i, 2], sh[i, 0] - sh[i, 6]);

    for (var i = 0; i < 3; i++)
        SHB[i] = new Vector4(sh[i, 4], sh[i, 5], sh[i, 6] * 3.0f, sh[i, 7]);

    SHC = new Vector4(sh[0, 8], sh[1, 8], sh[2, 8], 1);

    mat.SetVector("_SHAr", SHA[0]);
    mat.SetVector("_SHAg", SHA[1]);
    mat.SetVector("_SHAb", SHA[2]);
    mat.SetVector("_SHBr", SHB[0]);
    mat.SetVector("_SHBg", SHB[1]);
    mat.SetVector("_SHBb", SHB[2]);
    mat.SetVector("_SHC", SHC);
}

쉐이더의 SampleSH9 함수를 통해, SHCoefficient와 normal을 넘겨 적용해봅니다.

  
half4 frag(Varyings IN) : SV_Target
{
    IN.normal = normalize(IN.normal);

    //lambert
    Light light = GetMainLight();
    float lambertian = saturate(dot(IN.normal, light.direction));
    lambertian = lambertian * 0.5f + 0.5f;

    //BPhong
    float3 view = GetWorldSpaceNormalizeViewDir(IN.PositionWS);    //ShaderVariablesFunctions.hlsl
    float3 halfDirection = SafeNormalize(view + light.direction);  //common.hlsl
    
    float NoH = saturate(dot(halfDirection, IN.normal));
    half LoH = half(saturate(dot(light.direction, halfDirection)));

    //GGX
    float roughness2 = _Roughness * _Roughness;

    float d = NoH * NoH * (roughness2 - 1) + 1.00001f;
    half d2 = half(d * d);

    half LoH2 = LoH * LoH;
    half specularTerm = roughness2 / (d2 * max(half(0.1), LoH2) * (_Roughness * 4.0 + 2.0));
    
    //SH
    
    real4 SHCoefficients[7];
    SHCoefficients[0] = _SHAr;
    SHCoefficients[1] = _SHAg;
    SHCoefficients[2] = _SHAb;
    SHCoefficients[3] = _SHBr;
    SHCoefficients[4] = _SHBg;
    SHCoefficients[5] = _SHBb;
    SHCoefficients[6] = _SHC;

    half4 ambient = float4(SampleSH9(SHCoefficients, IN.normal), 1);
    return _BaseColor * lambertian + specularTerm + ambient;
}

Untitled

정확한 위치는 달라 SH값이 조금 다르지만,

유니티 URP에서 기본적으로 사용하는 Lit과 유사한 색감을 나타냅니다.

가져온 SH를 대신해 아무렇게나 작성한 SH값을 적는다면 다음과 같이 나타납니다.

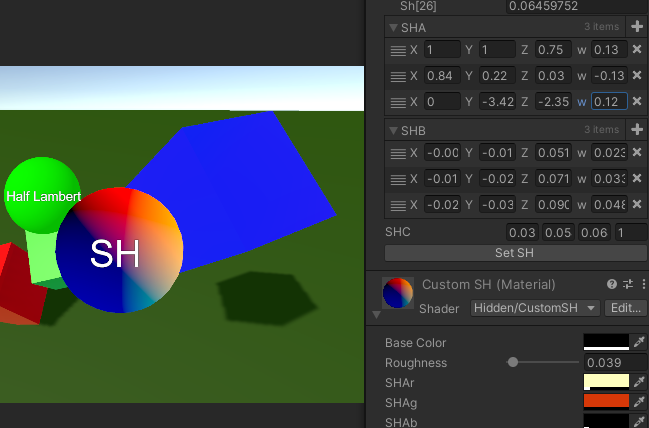아무 값이나 넣어본 결과

이는 나중에 어떤 값이 어떤 의미를 갖게되는지 확인할 것입니다.

더 깊게 들어가기 - 쉐이더 연산

SampleSH9 함수는 L0, L1, L2 의 합으로 구성되어 있습니다.

L0 & L1

L0은 상수니 계산식에서 합산하기 위해,

N, normal 이며 동시에 구체의 표면 방향에 대해 vector4의 w성분에 넣어 내적해줍니다.

내적은 ‘각 성분의 곱의 합’ 이므로,

w를 1로 둔 N,즉 표면방향과 내적한다면 L0인 상수값의 합을 최종적으로 같이 얻을 수 있게 됩니다.

구면조화함수의 기저함수가 어떻게 되어있든, 결국 xyz축을 사용하는 유클리드 공간에서는

L1의 기저가 X,Y,Z로 일반적으로 유니티에서 사용하는 기저와 같을 수 밖에 없습니다.

즉, 그저 normal N과의 내적으로 간단한 연산만으로 처리하기 위해

기저에 대한 rgb값을 세 기저에 대한 행렬로 뒀을때,

역행렬(기저는 직교이므로, 직교행렬)로 읽는다면 빠르게 내적처리할 수 있습니다.

원래는 다음과 같이 작성되어야 이해하기 편한 함수지만,

  
real3 SHEvalLinearL0L1(real3 N, real3 basisA, real3 basisB, real3 basisC, real3 l0)
{
    real4 vA = real4(N, 1.0);

    real3 x1;
    // Linear (L1) + constant (L0) polynomial terms
    x1.r = dot(real4(basisA.r, basisB.r, basisC.r, l0.r), vA);
    x1.g = dot(real4(basisA.g, basisB.g, basisC.g, l0.g), vA);
    x1.b = dot(real4(basisA.b, basisB.b, basisC.b, l0.b), vA);

    return x1;
}

아래와 같이 연산 최적화 된 것입니다.

  
real3 SHEvalLinearL0L1(real3 N, real4 shAr, real4 shAg, real4 shAb)
{
    real4 vA = real4(N, 1.0);

    real3 x1;
    // Linear (L1) + constant (L0) polynomial terms
    x1.r = dot(shAr, vA);
    x1.g = dot(shAg, vA);
    x1.b = dot(shAb, vA);

    return x1;
}

네이밍의 중요성을 다시한번 느끼게 됩니다. (SHa, SHb, SHc, SHd… 장난?)

사실 다른이름을 쓸 명칭도 없긴 한데 그냥 화가 납니다.

L2

Untitled

아까 위에서 봤던 기저를 다시 들고와서.

L1에서 사용한 방식인 각 채널에 대한 곱을 미리 스위즐링하여 계산된 벡터와 내적합니다.

그렇게 4개의 연산을 한번에 처리한 다음, 마지막 L22(l=2,m=2)에 대한 식을 계산해 더해줍니다.

  
real3 SHEvalLinearL2(real3 N, real4 shBr, real4 shBg, real4 shBb, real4 shC)
{
    real3 x2;
    // 4 of the quadratic (L2) polynomials
    real4 vB = N.xyzz * N.yzzx;
    x2.r = dot(shBr, vB);
    x2.g = dot(shBg, vB);
    x2.b = dot(shBb, vB);

    // Final (5th) quadratic (L2) polynomial
    real vC = N.x * N.x - N.y * N.y;
    real3 x3 = shC.rgb * vC;

    return x2 + x3;
}

L3

당연하게도 L3는 구현되어 있지 않지만,

위에서 확인한 L3다항식을 생각해본다면 못해볼것도 아닙니다.

  
real3 SHEvalLinearL3(real3 N, 
        real4 shDr, real4 shDg, real4 shDb, 
        real3 shEr, real3 shEg, real3 shEb)
{
    //-2 ~ 1
    real4 vD = N.xyxx * N.yyxz * N.xzxz;
    
    real3 vE = real3( 3 * N.x * N.x - N.y * N.y, //-3
        N.z * (N.x * N.x - N.y * N.y), //2
        N.x * (N.x * N.x - 3 * N.y * N.y)) //3
    
    
    real3 x3;
    x3.r = dot(shDr, vD);
    x3.g = dot(shDg, vD);
    x3.b = dot(shDb, vD);
    
    real3 x4;
    x4.r = dot(shEr, vE);
    x4.g = dot(shEg, vE);
    x4.b = dot(shEb, vE);
    return x3 + x4;
}

아마 이런식으로 구성되지 않을까 생각해봅니다.

Godot?

오픈소스 구현부를 확인해보겠습니다.

  
// read the spherical harmonic

	vec3 normal2 = normal * normal;
	float c[SH_SIZE] = float[](

			0.282095, //l0
			0.488603 * normal.y, //l1n1
			0.488603 * normal.z, //l1n0
			0.488603 * normal.x, //l1p1
			1.092548 * normal.x * normal.y, //l2n2
			1.092548 * normal.y * normal.z, //l2n1
			0.315392 * (3.0 * normal2.z - 1.0), //l20
			1.092548 * normal.x * normal.z, //l2p1
			0.546274 * (normal2.x - normal2.y) //l2p2
#if (SH_SIZE == 16)
			,
			0.590043 * normal.y * (3.0f * normal2.x - normal2.y),
			2.890611 * normal.y * normal.x * normal.z,
			0.646360 * normal.y * (-1.0f + 5.0f * normal2.z),
			0.373176 * (5.0f * normal2.z * normal.z - 3.0f * normal.z),
			0.457045 * normal.x * (-1.0f + 5.0f * normal2.z),
			1.445305 * (normal2.x - normal2.y) * normal.z,
			0.590043 * normal.x * (normal2.x - 3.0f * normal2.y)

#endif
	);

훨씬 더 정확하게 식을 사용하는것을 알 수 있습니다.

SH의 값?

  
public void SetSH()
{
    LightProbes.GetInterpolatedProbe(target.transform.position, target, out sh);
    
    for (var i = 0; i < 3; i++)
        SHA[i] = new Vector4(sh[i, 3], sh[i, 1], sh[i, 2], sh[i, 0] - sh[i, 6]);

    for (var i = 0; i < 3; i++)
        SHB[i] = new Vector4(sh[i, 4], sh[i, 5], sh[i, 6] * 3.0f, sh[i, 7]);

    SHC = new Vector4(sh[0, 8], sh[1, 8], sh[2, 8], 1);

    mat.SetVector("_SHAr", SHA[0]);
    mat.SetVector("_SHAg", SHA[1]);
    mat.SetVector("_SHAb", SHA[2]);
    mat.SetVector("_SHBr", SHB[0]);
    mat.SetVector("_SHBg", SHB[1]);
    mat.SetVector("_SHBb", SHB[2]);
    mat.SetVector("_SHC", SHC);
}

각 성분에 대한 정보는, 아까 쉐이더에서 확인한 기반으로

_SHA<채널> 각 기저의 대응하는 채널의 성분값 집합 (x = 기저1의 색상, … w = L0의 색상)

_SHB<채널> 각 기저의 대응하는 채널의 성분값 집합 (x = 기저1의 색상, … w = 기저4의 색상)

_SHC 각 기저의 대응하는 채널의 성분(x = 기저5의 R색상, z = 기저5의 B색상)

으로 확인할 수 있습니다.

트리비아

유니티를 뜯어보며 글을 작성하려했습니다.

하지만 유니티는 오픈소스가 아닙니다.

유니티를 뜯을 수 없다면 다른 엔진을 뜯으면 되는게 아닐까요?

이번엔 최근에 유니티 이슈와 함께 유명했던 Godot의 소스를 통해 알아보고싶었습니다.

유니티와 구현이 다를 수 있으니 참고로만 읽어주시면 좋겠다고 생각했었습니다.

**SphericalHarmonicsL2** 에는

Ambient Light를 추가하는것과

directional light를 추가하는 기능이 존재합니다.

하지만 실제로는 내부 **UnityEngine.CoreModule.dll**에 구현되어 있으므로, 확인할 수는 없습니다.

  
public void AddDirectionalLight(Vector3 direction, Color color, float intensity)
{
    var colorAndIntensity = color * (2.0f * intensity);
    AddDirectionalLightInternal(ref this, direction, colorAndIntensity);
}

[FreeFunction]
private extern static void AddDirectionalLightInternal(ref SphericalHarmonicsL2 sh, Vector3 direction, Color color);

언젠가 유니티가 오픈소스가 된다면 뜯어보도록 하죠.

Godot의 SH?

그러면 오픈소스인 Godot으로 뜯어보면 괜찮지않을까?

어림도없습니다 Godot은 SDFGI(Signed distance field global illumination)를 사용하며,

이에 대한 코멘트로

  
// converting to octahedral in this step is required because
// octahedral is much faster to read from the screen than spherical harmonics,
// despite the very slight quality loss

라고 말하고 있습니다. 솔직히 맞는말 갖긴 합니다.

유니티도겨우 L2 구면조화를 사용하는데 L3까지 지원하는 Godot에서 퀄리티를 조금 희생한다면

구면조화보다 연산이 빠른 8면체가 훨씬 나아보이니까요.

“증명이되었냐???” 라고 말씀하신다면 저는 godot엔진을 사용한 적 없어서 모릅니다.

작성자가 테스트했겠죠

구면조화의 회전

계수의 상수부에 대해서는 미리 계산해서 실수형태로 놔둘 수 있기 때문에,

먼저 계산해서 놔둡니다.

자세한건 아래코드를 확인해주세요.

  
void RotateSH(real_t *p_values) 
{
	// code by John Hable
	// this code is Public Domain

	const static real_t s_c3 = 0.94617469575; // (3*sqrt(5))/(4*sqrt(pi))
	const static real_t s_c4 = -0.31539156525; // (-sqrt(5))/(4*sqrt(pi))
	const static real_t s_c5 = 0.54627421529; // (sqrt(15))/(4*sqrt(pi))

	const static real_t s_c_scale = 1.0 / 0.91529123286551084;
	const static real_t s_c_scale_inv = 0.91529123286551084;

	const static real_t s_rc2 = 1.5853309190550713 * s_c_scale;
	const static real_t s_c4_div_c3 = s_c4 / s_c3;
	const static real_t s_c4_div_c3_x2 = (s_c4 / s_c3) * 2.0;

	const static real_t s_scale_dst2 = s_c3 * s_c_scale_inv;
	const static real_t s_scale_dst4 = s_c5 * s_c_scale_inv;

	const real_t src[9] = { p_values[0], p_values[1], p_values[2], p_values[3], p_values[4], p_values[5], p_values[6], p_values[7], p_values[8] };

	real_t m00 = rows[0][0];
	real_t m01 = rows[0][1];
	real_t m02 = rows[0][2];
	real_t m10 = rows[1][0];
	real_t m11 = rows[1][1];
	real_t m12 = rows[1][2];
	real_t m20 = rows[2][0];
	real_t m21 = rows[2][1];
	real_t m22 = rows[2][2];

	p_values[0] = src[0];
	p_values[1] = m11 * src[1] - m12 * src[2] + m10 * src[3];
	p_values[2] = -m21 * src[1] + m22 * src[2] - m20 * src[3];
	p_values[3] = m01 * src[1] - m02 * src[2] + m00 * src[3];

	real_t sh0 = src[7] + src[8] + src[8] - src[5];
	real_t sh1 = src[4] + s_rc2 * src[6] + src[7] + src[8];
	real_t sh2 = src[4];
	real_t sh3 = -src[7];
	real_t sh4 = -src[5];

	// Rotations.  R0 and R1 just use the raw matrix columns
	real_t r2x = m00 + m01;
	real_t r2y = m10 + m11;
	real_t r2z = m20 + m21;

	real_t r3x = m00 + m02;
	real_t r3y = m10 + m12;
	real_t r3z = m20 + m22;

	real_t r4x = m01 + m02;
	real_t r4y = m11 + m12;
	real_t r4z = m21 + m22;

	// dense matrix multiplication one column at a time

	// column 0
	real_t sh0_x = sh0 * m00;
	real_t sh0_y = sh0 * m10;
	real_t d0 = sh0_x * m10;
	real_t d1 = sh0_y * m20;
	real_t d2 = sh0 * (m20 * m20 + s_c4_div_c3);
	real_t d3 = sh0_x * m20;
	real_t d4 = sh0_x * m00 - sh0_y * m10;

	// column 1
	real_t sh1_x = sh1 * m02;
	real_t sh1_y = sh1 * m12;
	d0 += sh1_x * m12;
	d1 += sh1_y * m22;
	d2 += sh1 * (m22 * m22 + s_c4_div_c3);
	d3 += sh1_x * m22;
	d4 += sh1_x * m02 - sh1_y * m12;

	// column 2
	real_t sh2_x = sh2 * r2x;
	real_t sh2_y = sh2 * r2y;
	d0 += sh2_x * r2y;
	d1 += sh2_y * r2z;
	d2 += sh2 * (r2z * r2z + s_c4_div_c3_x2);
	d3 += sh2_x * r2z;
	d4 += sh2_x * r2x - sh2_y * r2y;

	// column 3
	real_t sh3_x = sh3 * r3x;
	real_t sh3_y = sh3 * r3y;
	d0 += sh3_x * r3y;
	d1 += sh3_y * r3z;
	d2 += sh3 * (r3z * r3z + s_c4_div_c3_x2);
	d3 += sh3_x * r3z;
	d4 += sh3_x * r3x - sh3_y * r3y;

	// column 4
	real_t sh4_x = sh4 * r4x;
	real_t sh4_y = sh4 * r4y;
	d0 += sh4_x * r4y;
	d1 += sh4_y * r4z;
	d2 += sh4 * (r4z * r4z + s_c4_div_c3_x2);
	d3 += sh4_x * r4z;
	d4 += sh4_x * r4x - sh4_y * r4y;

	// extra multipliers
	p_values[4] = d0;
	p_values[5] = -d1;
	p_values[6] = d2 * s_scale_dst2;
	p_values[7] = -d3;
	p_values[8] = d4 * s_scale_dst4;
}

참조

http://filmicworlds.com/blog/simple-and-fast-spherical-harmonic-rotation/

https://gdcvault.com/play/1015312/Light-Probe-Interpolation-Using-Tetrahedral

구면조화 (Spherical Harmonics)

여는장

1차원

2차원

3차원

조화 함수란?

구면조화(Spherical Harmonics)

구면조화는 왜 사용하나요?

구면조화의 특성

수학과 엔진적 측면

게임엔진에서의 구면조화

대역(차수)

시각화 및 기저

구면함수 - 계수(Coefficients)

구면함수 - 기저함수

구면함수 - 기저함수 - L2

구면함수 - 기저함수 - L3

사용해보기

엔진속 SH 꺼내쓰기

더 깊게 들어가기 - 쉐이더 연산

L0 & L1

L2

L3

Godot?

SH의 값?

트리비아

Godot의 SH?

구면조화의 회전

참조

Further Reading

Delaunay ShaderGraph

Covariance, Pearson Correlation Coefficient, Decorrelation

PBR(Physically Based Rendering)