아마 이 글은 2부작으로 작성될 예정입니다. 이건 빨리 쓰는데, 다음게 빡셉니다.
이미 작성한 줄 알고 열심히 블로그에서 검색하는데 안나오더라고요..
.. 어라 왜 분명 같은 내용을 쓴거같은 기억이.. 머리가..
머리
델로네,들로네,딜로네 등으로 불리는 Delaunay 삼각분할은 여러분야에서 사용되는 점 집합을 삼각형으로 나누는 방법 중 하나입니다. 저는 들로네라고 기술하겠습니다.
이 들로네 삼각분할은 뾰족한 삼각형을 최소한으로 생성하며,
어떤 삼각형의 외접원에도 다른점이 존재하지 않는 조건을 만족시킵니다.
저 조건은 최소각의 최대화를 꾀하며, 해당 삼각분할을 유일하게 만드며, 서로 가까운점들로 구성되도록 보장합니다. 그리고 또한 보로노이 다이어그램과 직접적인 관련이 있습니다.
보로노이 다이어그램(Voronoi)?
점 집합에 대해 평면을 나누는 방법입니다.
각 점에 대해 해당 점에서 가장 가까운 점들의 집합으로 구성된 영역을 생성하며, 이 영역인각 셀(cell)은 내부 점이 해당 셀의 생성 점에 다른 어떤 생성 점보다 더 가깝다는 특성을 갖습니다.
즉 어떤 선에서 가장 가까운 점을 이은 선분을 직교등분하는 선들로 이루어진 영역이라 볼 수 있으며, 이 선들은 들로네 삼각형의 변의 수직이등분선과 동일합니다. 그래서 관련이 있다는 것이죠
빈 외접원 속성(empty circumcircle property)의 고유성?
모든점이 평면에 있고 어떤 네점도 하나의 원 위에 위치하지 않는 경우(공존성,co-circularity)
해당 삼각분할은 유일하게 결정됩니다.
해당 특성은 보로노이 다이어그램과의 쌍대성, 삼각형의 극대 속성 등에 기반하여 계산기하학에서 일반적으로 받아들여진 결과입니다.
더 자세한 정보는 (위키피디아) 를 참조해주세요.
몸통
귀찮은 수학 얘기는 잘 안읽을테니 뒤로하고,
외접원 특성이 고유성을 나타내니 구현법이 다르더라도 같은 점집합에 대해 보로노이와 들로네는 쌍대성을 이루겠죠?
전체 알고리즘 흐름
- uv좌표를 Density를 통해 삼각분할을 수행할 공간으로 스케일링합니다.
- 각 셀에 대한 노이즈 오프셋[1]을 생성하고, 이에 랜덤점을 생성합니다.
- 중심점을 포함하는 쿼드를 구성해서 이를 기반으로 들로네 삼각분할을 수행합니다.
- 형성된 쿼드에 대해 가장 가까운 들로네 엣지를 찾고
- 뒤집힘 거리[2]를 기반으로 쿼드를 두 삼각형으로 분할한 뒤
- 가장 가까운 엣지까지의 거리와 엣지의 중심점을 결정합니다.
- 계산된 가장 가까운 거리와 중심점을 반환합니다.
노이즈[1]
보로노이와 들로네는 어찌되었든 노이즈벡터가 필요합니다.
점들의 위치를 변화시켜 좀 더 자연스러운 느낌을 주기 위해서입니다.
유니티 보로노이에서 사용하는 식과 동일한 식을 준비합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//https://docs.unity3d.com/Packages/com.unity.shadergraph@12.1/manual/Voronoi-Node.html
inline float2 unity_voronoi_noise_randomVector (float2 UV, float offset)
{
float2x2 m = float2x2(15.27, 47.63, 99.41, 89.98);
UV = frac(sin(mul(UV, m)) * 46839.32);
return float2(sin(UV.y*+offset)*0.5+0.5, cos(UV.x*offset)*0.5+0.5);
}
//Written Code
float2 delaunay_noise_randomVector(float2 UV, float offset)
{
float2x2 m = float2x2(15.27, 47.63, 99.41, 89.98);
UV = frac(sin(mul(UV, m)) * 46839.32);
return float2(sin(UV.y * offset), cos(UV.x * offset)) * 0.25;
}
선과의 거리 계산
선분거리계산은 내적을 사용합니다. 다만 재미있는부분이 저번에 쓸려다만건데
2차원 회전행렬중 90도 부분을 스위즐링과 부호를 통해 구할 수 있습니다. 시계방향으로 돌려줍니다.(90도 회전)
1
2
3
4
5
float distLine(float2 p0, float2 p1)
{
float2 e0 = p1 - p0;
return dot(p0, normalize(float2(e0.y, -e0.x)));
}
파라볼릭 리프팅[2]
https://sites.cs.ucsb.edu/~suri/cs235/Lifting.pdf
 파라볼로이드
파라볼로이드
2차원 문제를 3차원 공간에서의 볼록 껍질(Convex Hull) 문제로 변환해 두 삼각형이 뒤집힐 가능성을 계산합니다. 2차원 문제를 3차원에서 해결한다는 점에서 아핀 공간투영과 유사합니다.
핵심아이디어는 2차원 점을 3차원 위에 투영한다음, 투영한 점을 통과하는 평면의 방정식을 통해 들로네 조건을 검사합니다. (간단하겐, 면이 뒤집혀 있는지 검사합니다)
파라볼로이드의 기하학적 성질을 이해하면 아래의 방식을 이해할 수 있습니다.
- 파라볼로이드 표면 위의 점들은 원점으로부터의 거리가 증가함에 따라 높이가 빠르게 증가
- 이 표면은 모든 점에서 볼록(convex)함
- 볼록껍질의 조건에서는 세 점의 볼록껍질 면을 형성한다는 것은 세 점을 통과하는 평면이 세 모든 점을 한쪽에 두는 경우에만 성립.
볼록껍질(Convex Hull)의 기하학적 이해
- 반공간의 성질
- 임의의 평면에 의해 정의되는 반공간은 그 평면에 수직인 방향으로 무한히 확장. 평면은 공간을 ‘위’와 ‘아래’ 또는 ‘이쪽’과 ‘저쪽’으로 구분하는 경계 역할을 함.
- 볼록 껍질을 형성하는 점들은 특정 평면에 대해 모두 같은 반공간 내에 위치. 이는 볼록 껍질이 볼록성을 유지한다는 것을 의미하며, 볼록 껍질 내의 모든 점을 연결하는 선분이 항상 볼록 껍질 내부에 있음을 보장.
- 한쪽에만 두는 것의 의미:
- 평면에 의해 생성된 두 개의 반공간 중 하나가 집합 S0의 모든 점들을 포함하고, 다른 반공간은 포함하지 않는다는 것을 의미.
- 따라서 볼록 껍질은 집합의 모든 점들을 “감싸는” 볼록한 경계를 형성할 수 있음.
- 볼록성의 보장: 이 조건은 볼록 껍질이 볼록하다는 성질, 즉 껍질 내의 임의의 두 점을 잇는 선분이 항상 껍질 내에 위치한다는 성질을 보장합니다. 이는 볼록 껍질이 그 점들 사이의 “직선적인” 경로를 모두 포함한다는 것을 의미합니다.
(보조정리)파라볼로이드의 면 밑에 있는게 외접원과 무슨상관인가요?
평면내의 서로다른 네점을 고려하고 이들을 각각에 대응하는 파라볼로이드상의 투영에서(z= x^2 + y^2) 어느 특정점 s가 다른 세점의 외접원 내에 위치하는것은 특정점 s가 다른 세점을 통과하는 평면의 아래쪽에 위치하는 경우와만 동일.
이를 증명하기 위해 접평면의 방정식을 z값을 구하기 위한 식을 사용해 x,y를 미분,
양의 방향으로 p2만큼 이동시킨다면,
이 식은 원의 방정식과 같으므로 평면과 파라볼로이드의 교차는 공간곡선을 생성하며 이를 x,y 좌표계에 다시 투영하면 a,b를 중심으로 하는 원 이됨.
따라서 코드는?
…어쩌다 저 위가 저렇게 되었는지는 잘 모르겠지만
P=(x,y)를 P’(x,y,z) 로 투영하며, 이때 파라볼로이드에서 z = x^2 + y^2 이므로 둘을 내적,
z축을 따라 리프팅 한 후 이 점들을 통과하는 평면과 원점의 거리를 평면의 방정식을 통해 계산합니다. 이때 한 점(g1)과, 나머지 두 점(g2,g3)에 대한 위상차 외적의 결과는 평면의 법선벡터(노말)가 되므로, 처음 설정한 한 점과 법선벡터(노말)의 내적으로 구합니다.
즉 표면의 노말을 구하고, 노말과 점의 내적을 통해 면의 뒤집힘을 알 수 있으며, (ccw가 맞을지 cw가 맞을지 알 수 없으니까요)
양수이면 해당 삼각형이 들로네 조건을 만족합니다.
1
2
3
4
5
6
7
8
9
10
float flipDistance(float2 h1, float2 h2, float2 h3)
{
//paraboloid Projection .
float3 g1 = float3(h1.x, h1.y, dot(h1, h1));
float3 g2 = float3(h2.x, h2.y, dot(h2, h2));
float3 g3 = float3(h3.x, h3.y, dot(h3, h3));
//distance between plane and origin
return dot(g1, cross(g3 - g1, g2 - g1));
}
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#ifndef DELAUNAY_TRIANGULATION
#define DELAUNAY_TRIANGULATION
float2 delaunay_noise_randomVector(float2 UV, float offset)
{
float2x2 m = float2x2(15.27, 47.63, 99.41, 89.98);
UV = frac(sin(mul(UV, m)) * 46839.32);
return float2(sin(UV.y * offset), cos(UV.x * offset)) * 0.25;
}
float distLine(float2 p0, float2 p1)
{
float2 e0 = p1 - p0;
return dot(p0, normalize(float2(e0.y, -e0.x)));
}
//backface test
float flipDistance(float2 h1, float2 h2, float2 h3)
{
//paraboloid Projection.
float3 g1 = float3(h1.x, h1.y, dot(h1, h1));
float3 g2 = float3(h2.x, h2.y, dot(h2, h2));
float3 g3 = float3(h3.x, h3.y, dot(h3, h3));
//distance between plane and origin
return dot(g1, cross(g3 - g1, g2 - g1));
}
void delaunayQuad(float2 h0, float2 h1, float2 h2, float2 h3, float2 pos0, float2 pos1, float2 pos2, float2 pos3, inout float distance, inout float2 center)
{
float minDistance = min(min(distLine(h0, h1), distLine(h1, h2)), min(distLine(h2, h3), distLine(h3, h0)));
// Outside the quad
if (minDistance < 0.0)
return;
// diagonal distance Check
float dc = flipDistance(h0 - h2, h1 - h2, h3 - h2);
float2 diagonalPosition0 = (dc > 0.0) ? h3 : h0;
float2 diagonalPosition1 = (dc > 0.0) ? h1 : h2;
float distToDiagonal = distLine(diagonalPosition0, diagonalPosition1);
minDistance = min(minDistance, abs(distToDiagonal));
distance = min(minDistance, distance);
if (dc > 0.0)
{
if (distToDiagonal > 0.0)
center = (pos1 + pos2 + pos3) / 3.0;
else
center = (pos0 + pos1 + pos3) / 3.0;
}
else
{
if (distToDiagonal > 0.0)
center = (pos0 + pos2 + pos3) / 3.0;
else
center = (pos0 + pos1 + pos2) / 3.0;
}
}
// Final function visits 4 quads around the center cell.
void delaunayTriangulation(float2 UV, float AngleOffset, out float minDistance, out float2 center)
{
float2 grid = floor(UV);
// Cache sites coordinate.
float2 site[9];
float2 h[9];
// Iterate sites.
for (int y = -1; y <= 1; y++)
{
for (int x = -1; x <= 1; x++)
{
float2 lattice = float2(x, y);
float2 offset = float2(0.5, 0.5) + delaunay_noise_randomVector(grid + lattice, AngleOffset);
site[(x + 1) + (y + 1) * 3] = grid + lattice + offset;
h[(x + 1) + (y + 1) * 3] = site[(x + 1) + (y + 1) * 3] - UV;
}
}
minDistance = 8.0;
center = float2(0.0, 0.0);
delaunayQuad(h[3], h[0], h[1], h[4], site[3], site[0], site[1], site[4], minDistance, center);
delaunayQuad(h[4], h[1], h[2], h[5], site[4], site[1], site[2], site[5], minDistance, center);
delaunayQuad(h[7], h[4], h[5], h[8], site[7], site[4], site[5], site[8], minDistance, center);
delaunayQuad(h[6], h[3], h[4], h[7], site[6], site[3], site[4], site[7], minDistance, center);
}
void Unity_Delaunay_Triangulation_float(float2 UV, float AngleOffset, float CellDensity, out float Out, out float2 Cells)
{
delaunayTriangulation(UV * CellDensity, AngleOffset, Out, Cells);
}
#endif // DELAUNAY_TRIANGULATION
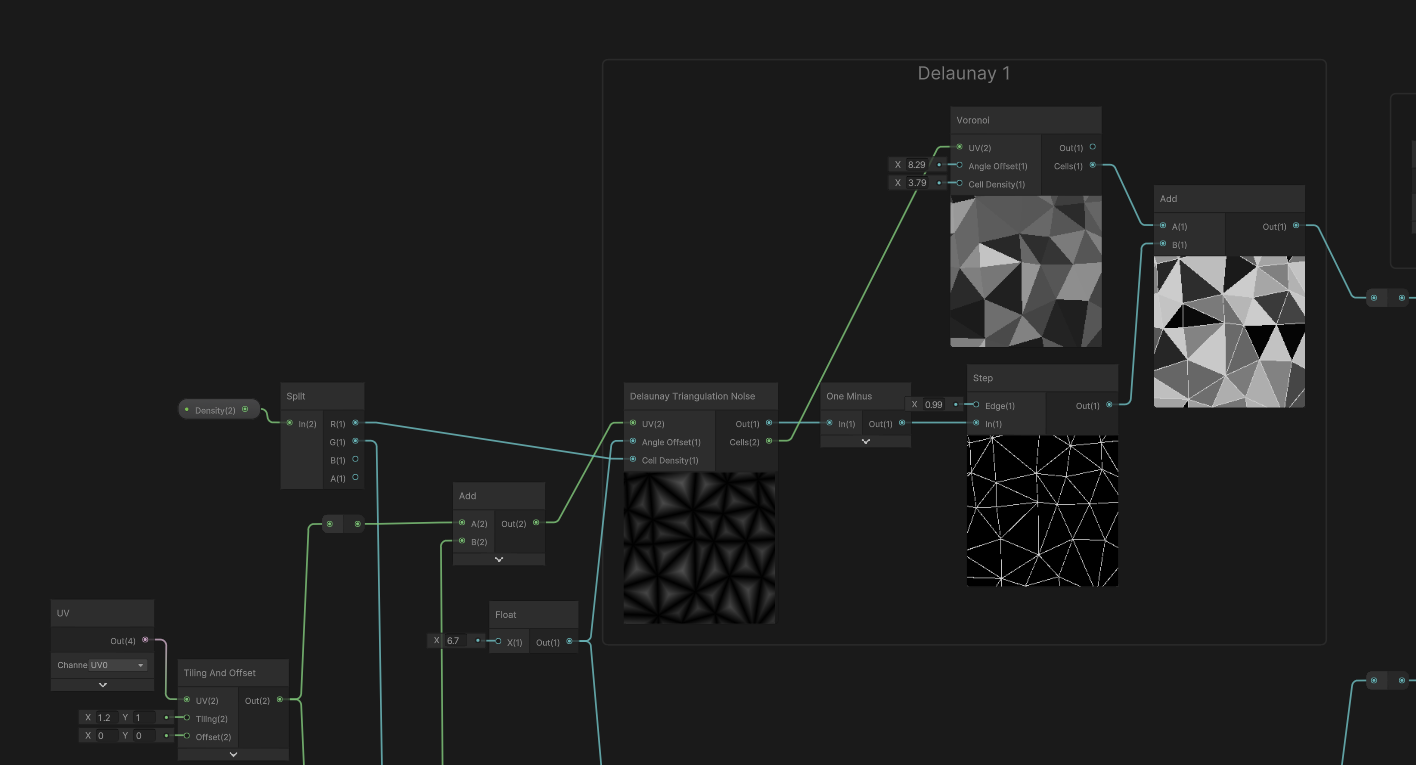
몸통 - 쉐이더그래프
맨 마지막 함수를 보면 알 수 있듯 사실 ShaderGraph를 위해 만들어진 코드입니다.
삼각분할을 할 수 있다면 크리스탈과 비슷한 느낌을 낼 수 있겟죠?
보로노이로도 그런 느낌을 낼 수 있기는하지만, 보로노이는 삼각분할과는 다릅니다.
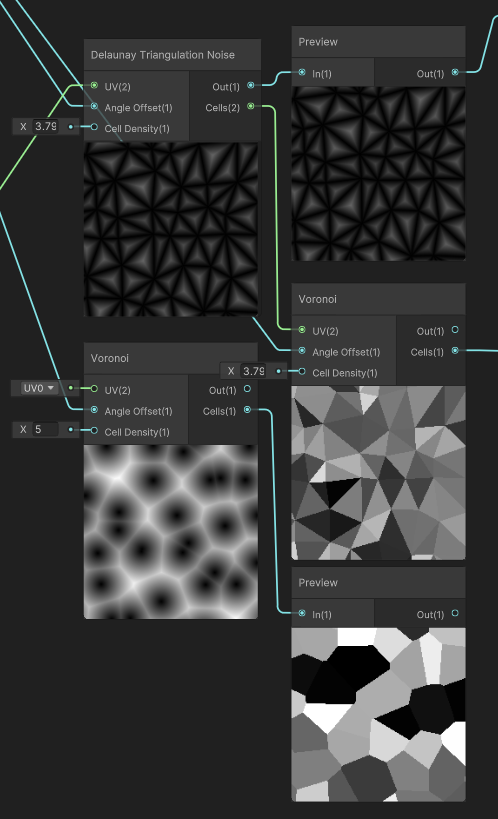
삼각분할을 사용한 후 셀값을 보로이의 uv로 전달하면,
삼각형의 각 영역의 셀값을 구할 수 얻을 수 있고,
out값을 역전해 step을 통해 선을 얻어올 수 있습니다.
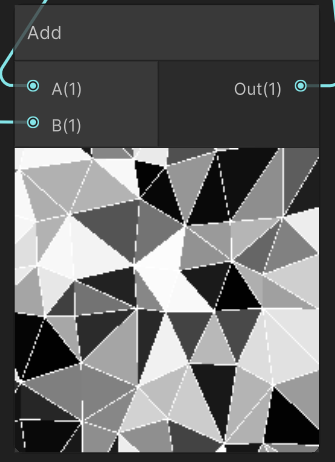
섞으면 이런느낌이죠
해당값을 리맵해서 노멀벡터를 조금 이동시켜 화면 위치를 굴절시키면
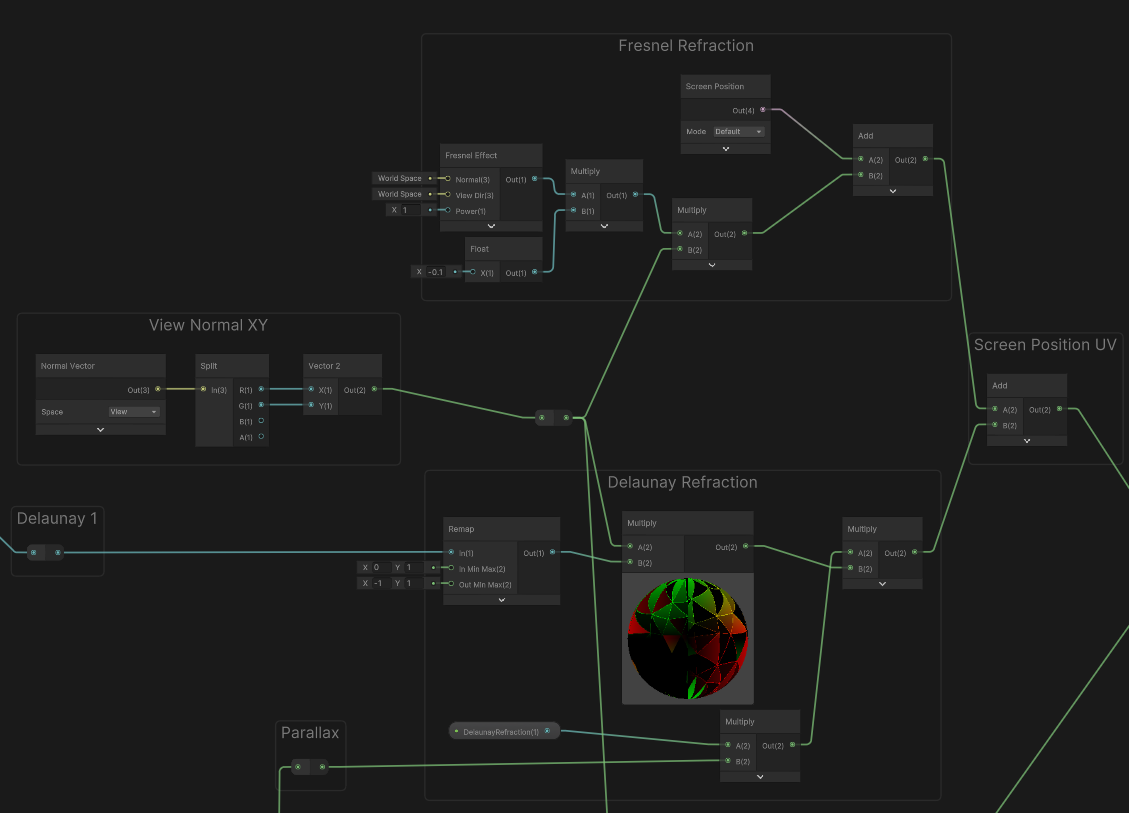

이런 굴절느낌을 얻을 수 있습니다 .
하지만 너무 평면적이므로 마음에 들지 않으니
패럴랙스를 섞어서
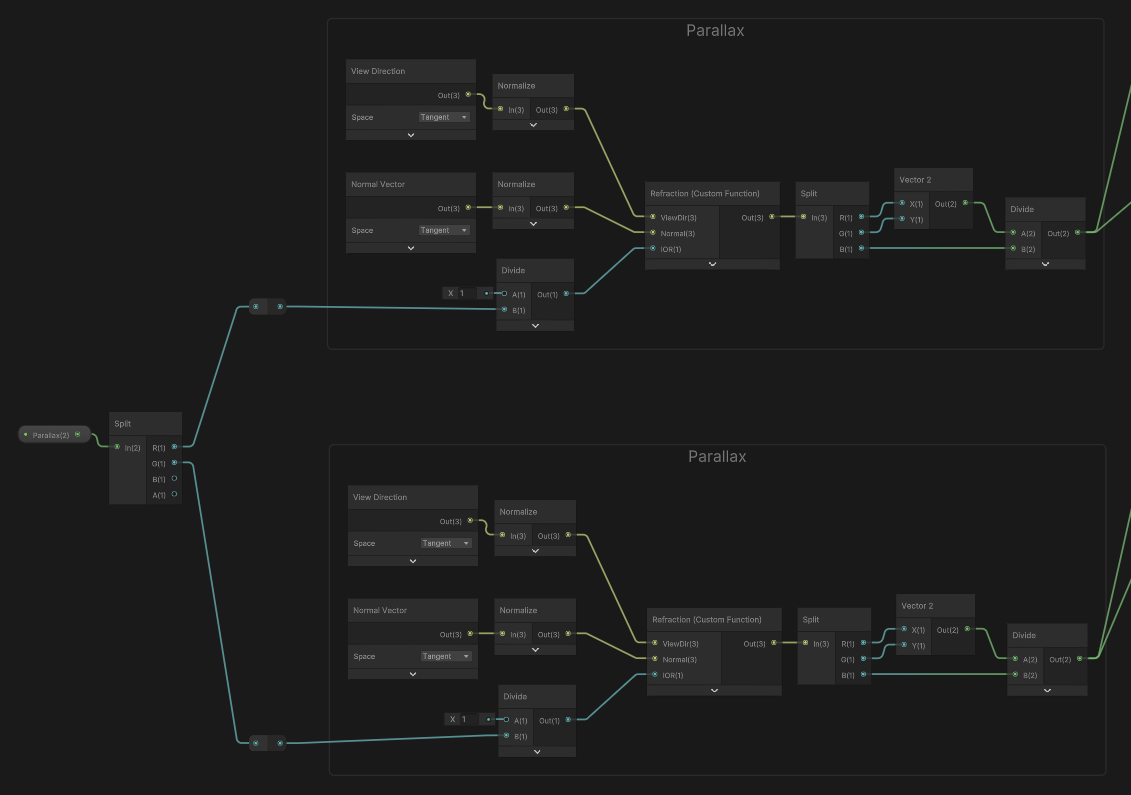
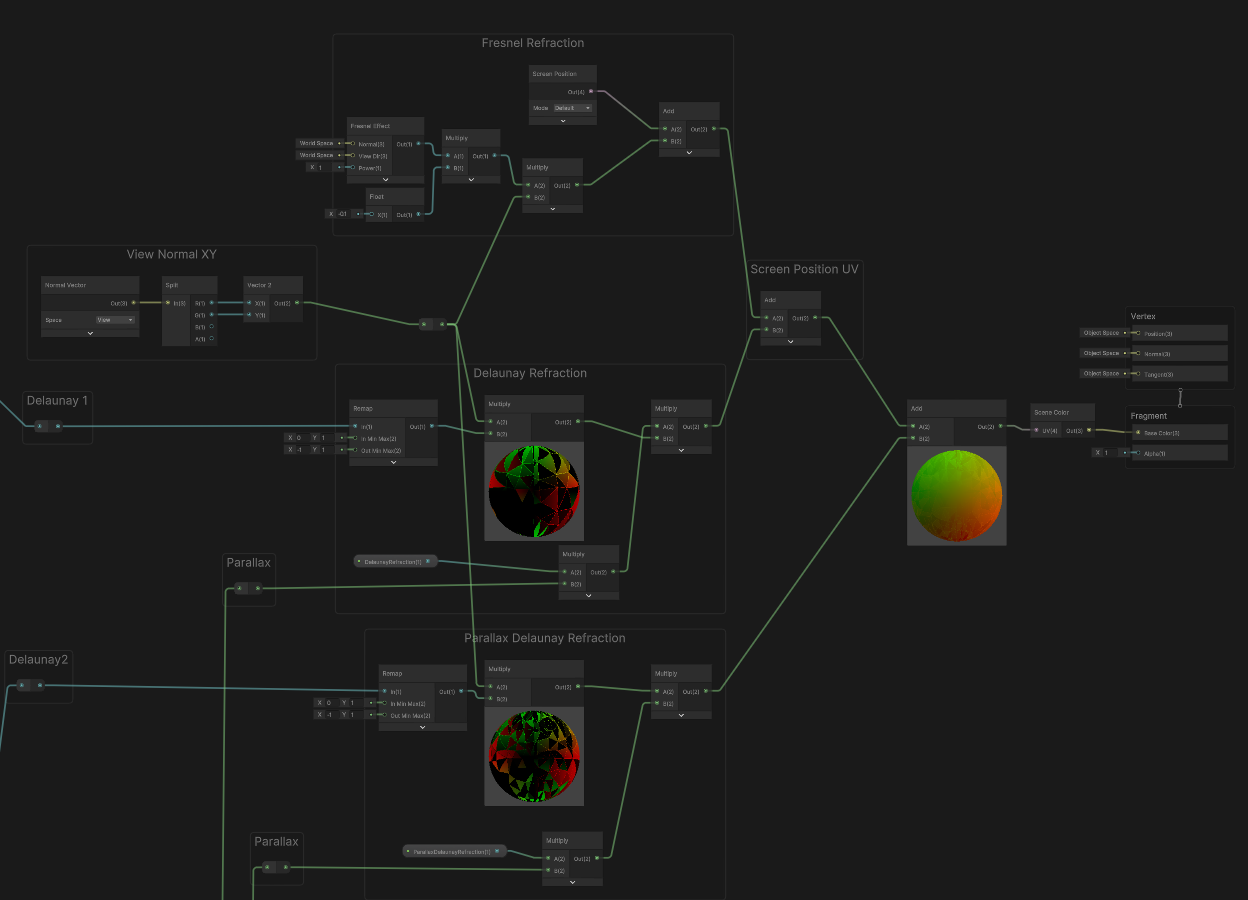

조금더 입체의 느낌을 낼 수 있습니다.
꼬리


생각보다 이쁘게 나온 것 같아 좋습니다.
이렇게까지 쓸 예정이 아니였는데 파고들다보니 수학이 많네요.
은근슬쩍 math태그를 추가했습니다.
